高中3.2 函数的基本性质第2课时学案及答案

这是一份高中3.2 函数的基本性质第2课时学案及答案，共15页。
1．理解函数的最大(小)值的概念及其几何意义．
2．会借助单调性求最值．
3．掌握求二次函数在闭区间上的最值．
1．最大值
(1)定义：一般地，设函数y＝f(x)的定义域为I，如果存在实数M满足：
①∀x∈I，都有f(x)≤M；
②∃x0∈I，使得f(x0)＝M.
那么，称M是函数y＝f(x)的最大值．
(2)几何意义：函数y＝f(x)的最大值是图象最高点的纵坐标．
2．最小值
(1)定义：一般地，设函数y＝f(x)的定义域为I，如果存在实数M满足：
①∀x∈I，都有f(x)≥M；
②∃x0∈I，使得f(x0)＝M.
那么，称M是函数y＝f(x)的最小值．
(2)几何意义：函数y＝f(x)的最小值是图象最低点的纵坐标．
温馨提示：(1)最大(小)值必须是一个函数值，是值域中的一个元素．
(2)并不是每一个函数都有最值，如函数y＝eq \f(1,x)，既没有最大值，也没有最小值．
(3)最值是函数的整体性质，即在函数的整个定义域内研究其最值．
1．函数y＝f(x)在[－2,2]上的图象如图所示，试指出此函数的最小值、最大值和相应的x的值．
[答案] f(x)的最小值为－1，此时x＝－2；
f(x)的最大值为2，此时x＝1
2．判断正误(正确的打“√”，错误的打“×”)
(1)任何函数都有最大值或最小值．( )
(2)函数的最小值一定比最大值小．( )
(3)函数f(x)＝－x在[2,3)上的最大值为－2，无最小值．( )
(4)函数最大值对应图象中的最高点，且该点只有一个．( )
[答案] (1)× (2)× (3)√ (4)×
题型一 图象法求函数的最大(小)值
【典例1】 (1)已知函数f(x)＝eq \b\lc\{\rc\ (\a\vs4\al\c1(x2，－1≤x≤1，,\f(1,x)，x>1.))求f(x)的最大值、最小值；
(2)画出函数f(x)＝eq \b\lc\{\rc\ (\a\vs4\al\c1(－\f(2,x)，x∈－∞，0，,x2＋2x－1，x∈[0，＋∞))的图象，并写出函数的单调区间，函数的最小值．
[思路导引] 作出函数f(x)的图象，结合图象求解．
[解] (1)作出函数f(x)的图象(如图1)．
由图象可知，当x＝±1时，f(x)取最大值为f(±1)＝1；当x＝0时，f(x)取最小值f(0)＝0，故f(x)的最大值为1，最小值为0.
(2)f(x)的图象如图2所示，f(x)的单调递增区间是(－∞，0)和[0，＋∞)，函数的最小值为f(0)＝－1.
图象法求最大(小)值的步骤
[针对训练]
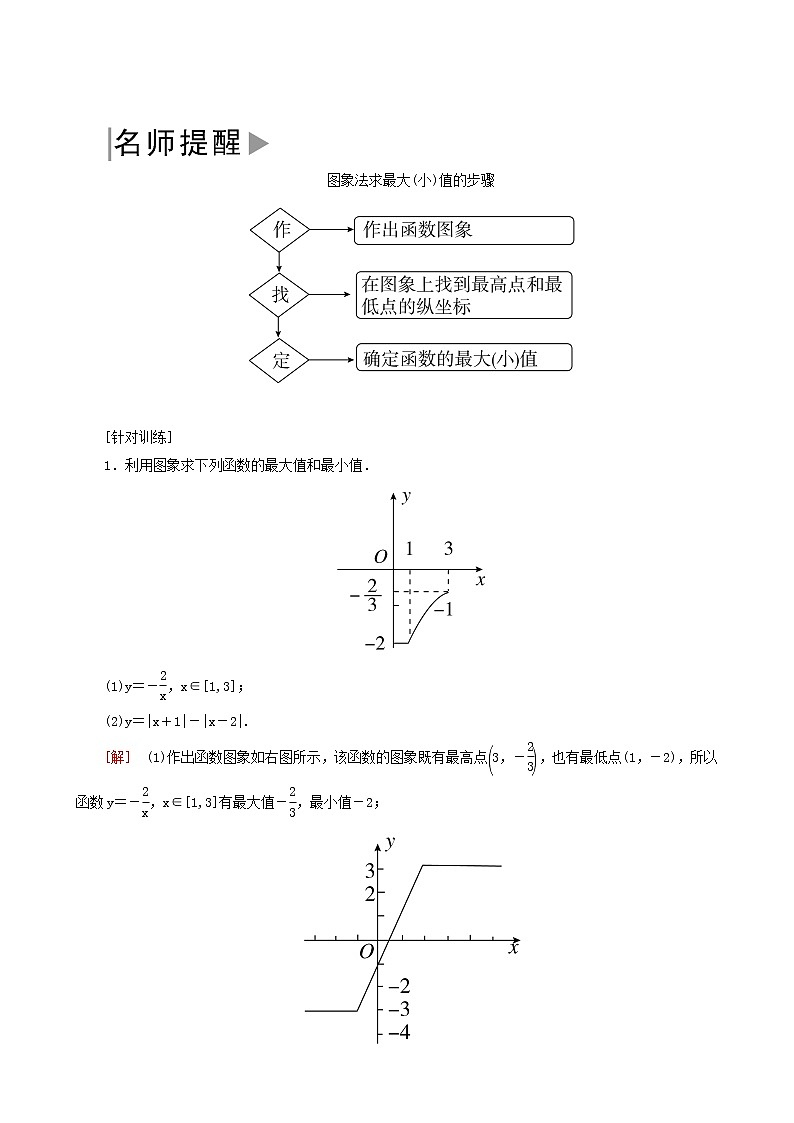
1．利用图象求下列函数的最大值和最小值．
(1)y＝－eq \f(2,x)，x∈[1,3]；
(2)y＝|x＋1|－|x－2|.
[解] (1)作出函数图象如右图所示，该函数的图象既有最高点eq \b\lc\(\rc\)(\a\vs4\al\c1(3，－\f(2,3)))，也有最低点(1，－2)，所以函数y＝－eq \f(2,x)，x∈[1,3]有最大值－eq \f(2,3)，最小值－2；
(2)y＝|x＋1|－|x－2|
＝eq \b\lc\{\rc\ (\a\vs4\al\c1(3，x≥2，,2x－1，－10，
故(x1－x2)·eq \f(x1x2－1,x1x2)400时，f(x)＝60000－100x是减函数，f(x)1时，f(x)在[－1,1]上单调递减，
故f(x)min＝f(1)＝3－2a；
②当－1≤a≤1时，f(x)在[－1,1]上先减后增，
故f(x)min＝f(a)＝2－a2；
③当a1，,2－a2，－1≤a≤1，,3＋2a，a0时，f(x)0时，f(x)