人教A版 (2019)必修 第一册第四章 指数函数与对数函数4.4 对数函数第1课时导学案

  4．4　对数函数

第1课时　对数函数及其图象

1．理解对数函数的概念．

2．掌握对数函数的图象和简单性质．

3．了解对数函数在生产实际中的简单应用．

1．对数函数的概念

函数y＝logax(a>0，且a≠1)叫做对数函数，其中x是自变量，函数的定义域是(0，＋∞)．

温馨提示：(1)对数函数y＝logax是由指数函数y＝ax反解后将x、y互换得到的．

(2)无论是指数函数还是对数函数，都有其底数a>0且a≠1.

2．对数函数的图象及性质

温馨提示：底数a与1的大小关系决定了对数函数图象的“升降”：当a>1时，对数函数的图象“上升”；当0<a<1时，对数函数的图象“下降”．

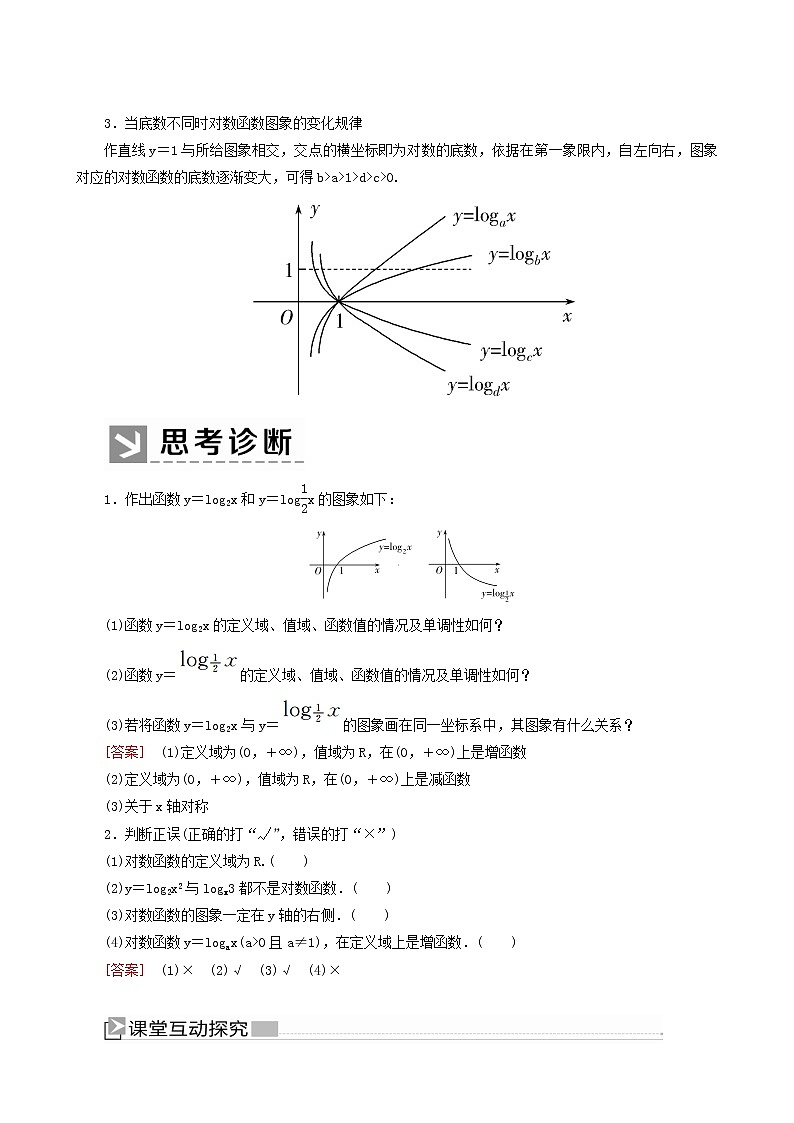
3．当底数不同时对数函数图象的变化规律

作直线y＝1与所给图象相交，交点的横坐标即为对数的底数，依据在第一象限内，自左向右，图象对应的对数函数的底数逐渐变大，可得b>a>1>d>c>0.

1．作出函数y＝log2x和y＝logx的图象如下：

(1)函数y＝log2x的定义域、值域、函数值的情况及单调性如何？

(2)函数y＝的定义域、值域、函数值的情况及单调性如何？

(3)若将函数y＝log2x与y＝的图象画在同一坐标系中，其图象有什么关系？

[答案]　(1)定义域为(0，＋∞)，值域为R，在(0，＋∞)上是增函数

(2)定义域为(0，＋∞)，值域为R，在(0，＋∞)上是减函数

(3)关于x轴对称

2．判断正误(正确的打“√”，错误的打“×”)

(1)对数函数的定义域为R.(　　)

(2)y＝log2x2与logx3都不是对数函数．(　　)

(3)对数函数的图象一定在y轴的右侧．(　　)

(4)对数函数y＝logax(a>0且a≠1)，在定义域上是增函数．(　　)

[答案]　(1)×　(2)√　(3)√　(4)×

题型一  对数函数的概念

【典例1】　指出下列函数哪些是对数函数？

(1)y＝3log2x；(2)y＝log6x；

(3)y＝logx3；(4)y＝log2x＋1.

[思路导引]　紧扣对数函数的定义判断．

[解]　(1)log2x的系数是3，不是1，不是对数函数．

(2)符合对数函数的结构形式，是对数函数．

(3)自变量在底数位置上，不是对数函数．

(4)对数式log2x后又加1，不是对数函数．

　依据3个形式特点判断对数函数

判断一个函数是对数函数必须是形如y＝logax(a>0且a≠1)的形式，即必须满足以下条件：

(1)系数为1.

(2)底数为大于0且不等于1的常数．

(3)对数的真数仅有自变量x.

[针对训练]

1．若对数函数y＝f(x)满足f(4)＝2，则该对数函数的解析式为(　　)

A．y＝log2x B．y＝2log4x

C．y＝log2x或y＝2log4x D．不确定

[解析]　设对数函数的解析式为y＝logax(a>0，且a≠1)，由题意可知loga4＝2，

∴a2＝4，∴a＝2.

∴该对数函数的解析式为y＝log2x.

[答案]　A

题型二  对数型函数的定义域

【典例2】　求下列函数的定义域．

(1)y＝；(2)y＝；

(3)y＝；(4)y＝log(x＋1)(2－x)．

[解]　(1)定义域为(0，＋∞)．

(2)由解得<x≤1，

∴定义域为.

(3)由解得<x≤，

∴定义域为.

(4)由解得－1<x<0或0<x<2，

∴定义域为(－1,0)∪(0,2)．

　求对数函数定义域的注意事项

求与对数函数有关的函数定义域时，除遵循前面已学习过的求函数定义域的方法外，还要对这种函数自身有如下要求：一是要特别注意真数大于零；二是要注意对数的底数大于零且不等于1.

[针对训练]

2．求下列函数的定义域．

(1)y＝；(2)y＝；

(3)y＝(a>0且a≠1)．

[解]　(1)解得1<x≤2

∴定义域为{x|1<x≤2}．

(2)解得1<x<2

∴定义域为{x|1<x<2}．

(3)当0<a<1时，0<4x－3≤1⇒<x≤1，∴定义域为；

当a>1时，4x－3≥1⇒x≥1，∴定义域为{x|x≥1}.

题型三  对数函数的图象

【典例3】　(1)已知a>0，且a≠1，则函数y＝ax与y＝

loga(－x)的图象只能是(　　)

(2)函数y＝loga(x＋1)－2(a>0，且a≠1)的图象恒过点________．

[思路导引]　利用对数函数的图象特征求解．

[解析]　(1)解法一：若0<a<1，则函数y＝ax的图象下降且过点(0,1)，而函数y＝loga(－x)的图象上升且过点(－1,0)，以上图象均不符合．若a>1，则函数y＝ax的图象上升且过点(0,1)，而函数y＝loga(－x)的图象下降且过点(－1,0)，只有B中图象符合．

解法二：首先指数函数y＝ax的图象只可能在上半平面，函数y＝loga(－x)的图象只可能在左半平面，从而排除A、C；再看单调性，y＝ax与y＝loga(－x)的单调性正好相反，排除D.只有B中图象符合．

(2)因为函数y＝logax (a>0，且a≠1)的图象恒过点(1,0)，则令x＋1＝1得x＝0，此时y＝loga(x＋1)－2＝－2，所以函数y＝loga(x＋1)－2(a>0，且a≠1)的图象恒过点(0，－2)．

[答案]　(1)B　(2)(0，－2)

[变式]　若本例(2)的函数改为“y＝loga＋2”，则图象恒过定点坐标是________．

[解析]　令＝1，得x＝－2，此时y＝2，

∴函数y＝loga＋2过定点(－2,2)．

[答案]　(－2,2)

　处理对数函数图象问题的3个注意点

(1)明确图象的分布区域．对数函数的图象在第一、四象限．当x趋近于0时，函数图象会越来越靠近y轴，但永远不会与y轴相交．

(2)建立分类讨论的思想．在画对数函数图象之前要先判断对数的底数a的取值范围是a>1，还是0<a<1.

(3)牢记特殊点．对数函数y＝logax(a>0，且a≠1)的图象经过点：(1,0)，(a,1)和.

[针对训练]

3．函数y＝lg(x＋1)的图象大致是(　　)

[解析]　由底数大于1可排除A、B，y＝lg(x＋1)可看作是y＝lgx的图象向左平移1个单位．(或令x＝0得y＝0，而且函数为增函数)

[答案]　C

4.如图，若C1，C2分别为函数y＝logax和y＝logbx的图象，则(　　)

A．0<a<b<1

B．0<b<a<1

C．a>b>1

D．b>a>1

[解析]　作直线y＝1，则直线与C1，C2的交点的横坐标分别为a，b，易知0<b<a<1.

[答案]　B

1．对数函数的图象过点M(16,4)，则此对数函数的解析式为(　　)

[解析]　设对数函数为y＝logax(a>0，且a≠1)，由于对数函数的图象过点M(16,4)，所以4＝loga16，得a＝2.所以对数函数的解析式为y＝log2x，故选D.

[答案]　D

2．若f(x)＝，则f(x)的定义域为(　　)

A.   B.∪(0，＋∞)

C.   D.

[解析]　根据题意得解得x∈∪(0，＋∞)．故选B.

[答案]　B

3．若函数f(x)是定义在R上的奇函数，f＝1，当x<0时，f(x)＝log2(－x)＋m，则实数m＝(　　)

A．－1 B．0 

C．1 D．2

[解析]　∵f(x)是定义在R上的奇函数，f＝1，且x<0时，f(x)＝log2(－x)＋m，

∴f＝log2＋m＝－2＋m＝－1，∴m＝1.故选C.

[答案]　C

4．已知函数y＝loga(x－3)－1的图象恒过定点P，则点P的坐标是________．

[解析]　y＝logax的图象恒过点(1,0)，令x－3＝1，得x＝4，则y＝－1.

[答案]　(4，－1)

5．已知f(x)＝loga|x|，满足f(－5)＝1，试画出函数f(x)的图象．

[解]　因为f(－5)＝1，所以loga5＝1，即a＝5，故f(x)＝log5|x|＝

所以函数y＝log5|x|的图象如下图所示．

课后作业(三十一)

复习巩固

一、选择题

1．设函数f(x)＝则f(－2)＋f(log212)＝(　　)

A．3 B．6 

C．9 D．12

[解析]　由于f(－2)＝1＋log24＝3，f(log212)＝＝6，所以f(－2)＋f(log212)＝9.故选C.

[答案]　C

2．函数y＝loga(3x－2)(a>0，a≠1)的图象过定点(　　)

A. B．(1,0)

C．(0,1)   D.

[解析]　根据对数函数过定点(1,0)，令3x－2＝1，得x＝1，∴过定点(1,0)．

[答案]　B

3．函数f(x)＝log2(x2＋8)的值域为(　　)

A．R B．[0，＋∞)

C．[3，＋∞) D．(－∞，3]

[解析]　设t＝x2＋8，则t≥8，又函数y＝log2t在(0，＋∞)上为增函数，所以f(x)≥log28＝3.故选C.

[答案]　C

4．已知m，n∈R，函数f(x)＝m＋lognx的图象如右图，则m，n的取值范围分别是(　　)

A．m>0,0<n<1  　　B．m<0,0<n<1

C．m>0，n>1  　　D．m<0，n>1

[解析]　由图象知函数为增函数，故n>1.

又当x＝1时，f(x)＝m>0，故m>0.

[答案]　C

5．已知函数f(x)＝alog2x＋blog3x＋2，且f＝4，则f(2019)的值为(　　)

A．－4 B．－2 

C．0 D．2

[解析]　f(x)＋f＝alog2x＋blog3x＋2＋alog2＋blog3＋2＝4，所以f(2019)＋f＝4，又因为f＝4，所以f(2019)＝0.

[答案]　C

二、填空题

6．函数f(x)＝的定义域为________．

[解析]　由1－2log5x≥0，得log5x≤，故0<x≤.

[答案]　(0，]

7．函数f(x)＝loga(x＋2)＋3(a>0，且a≠1)的图象恒过定点________．

[解析]　令x＋2＝1，解得x＝－1.因为f(－1)＝3，所以f(x)的图象恒过定点(－1,3)．

[答案]　(－1,3)

8．若f(x)是对数函数且f(9)＝2，当x∈[1,3]时，f(x)的值域是________．

[解析]　设f(x)＝logax，因为loga9＝2，所以a＝3，即f(x)＝log3x.又因为x∈[1,3]，所以0≤f(x)≤1.

[答案]　[0,1]

三、解答题

9．若函数y＝loga(x＋a)(a>0且a≠1)的图象过点(－1,0)．

(1)求a的值；

(2)求函数的定义域．

[解]　(1)将(－1,0)代入y＝loga(x＋a)(a>0，且a≠1)中，有0＝loga(－1＋a)，则－1＋a＝1，所以a＝2.

(2)由(1)知y＝log2(x＋2)，由x＋2>0，解得x>－2，

所以函数的定义域为{x|x>－2}．

10．若函数f(x)为定义在R上的奇函数，且x∈(0，＋∞)时，f(x)＝lg(x＋1)，求f(x)的表达式，并画出大致图象．

[解]　∵f(x)为R上的奇函数，∴f(0)＝0.

又当x∈(－∞，0)时，－x∈(0，＋∞)，

∴f(－x)＝lg(1－x)．

又f(－x)＝－f(x)，∴f(x)＝－lg(1－x)，

∴f(x)的解析式为f(x)

＝

f(x)的大致图象如图所示．

综合运用

11．已知函数f(x)＝那么f的值为(　　)

A．27　　　B.　　　C．－27　　　D．－

[解析]　f＝log2＝log22－3＝－3，

f＝f(－3)＝3－3＝.

[答案]　B

12．下列函数中，值域是[0，＋∞)的是(　　)

A．f(x)＝log2(x－1) B．f(x)＝

C．f(x)＝log2(x2＋2) D．f(x)＝log2

[解析]　A、D中因为真数大于0，故值域为R，C中因为x2＋2≥2，故f(x)≥1.只有B中log2(x－1)≥0，f(x)的值域为[0，＋∞)．

[答案]　B

13．若函数f(x)＝loga(x＋b)的图象如图，其中a，b为常数，则函数g(x)＝ax＋b的图象大致是(　　)

[解析]　由函数f(x)＝loga(x＋b)的图象可知，函数f(x)＝loga(x＋b)在(－b，＋∞)上是减函数．

∴0<a<1且0<b<1.所以g(x)＝ax＋b在R上是减函数，故排除A、B.由g(x)的值域为(b，＋∞)．所以g(x)＝ax＋b的图象应在直线y＝b的上方，故排除C.

[答案]　D

14．设函数f(x)＝logax(a>0，且a≠1)，若f(x1x2…x2019)＝8，则f(x)＋f(x)＋f(x)＋…＋f(x)的值等于________．

[解析]　∵f(x)＋f(x)＋f(x)＋…＋f(x)

＝logax＋logax＋logax＋…＋logax

＝loga(x1x2x3…x2019)2

＝2loga(x1x2x3…x2019)

＝2f(x1x2x3…x2019)，

∴原式＝2×8＝16.

[答案]　16

15．已知函数f(x)＝的定义域为，值域为[0,1]，则m的取值范围为________．

[解析]　

作出f(x)＝的图象(如图)可知f＝f(2)＝1，f(1)＝0，由题意结合图象知：1≤m≤2.

[答案]　[1,2]

16．已知函数f(x)＝loga(x－1)的图象过点(3,1)．

(1)求函数f(x)的解析式；

(2)若f(m)≤f(2)，求m的取值集合．

[解]　(1)由函数f(x)＝loga(x－1)的图象过点(3,1)，得a＝2.所以函数解析式为f(x)＝log2(x－1)．

(2)若f(m)≤f(2)，由f(x)在(1，＋∞)上单调递增，得1<m≤2.

所以m的取值集合为{m|1<m≤2}．