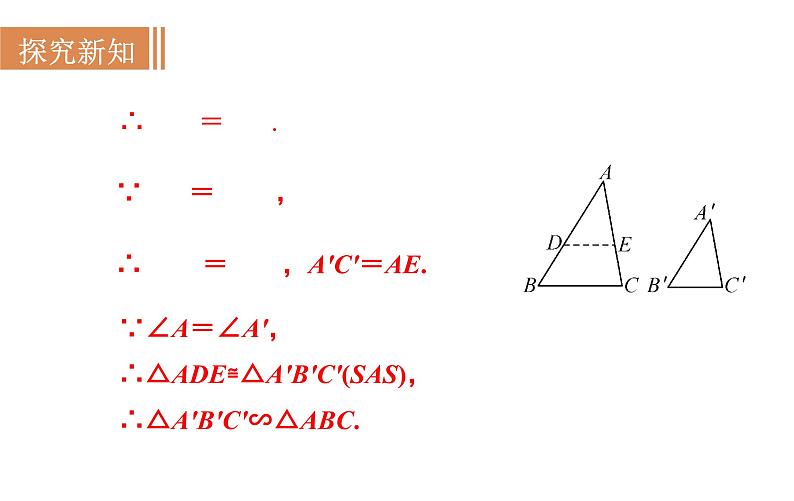
数学九年级上册22.2 相似三角形的判定图片课件ppt

这是一份数学九年级上册22.2 相似三角形的判定图片课件ppt，共24页。PPT课件主要包含了旧知回顾，通过定义不常用，观察与思考，不相似，∵∠A＝∠A′，练一练，解若∠B＝∠C，又∵∠B∠ACD等内容，欢迎下载使用。

1．相似三角形的定义是什么？
三边成比例，三角分别相等的两个三角形相似．
2．判定两个三角形相似，你有哪些方法？
通过平行线(条件特殊，使用起来有局限性)；
判定定理1，两角分别相等的两个三角形相似(不需要边的条件、使用灵活)．
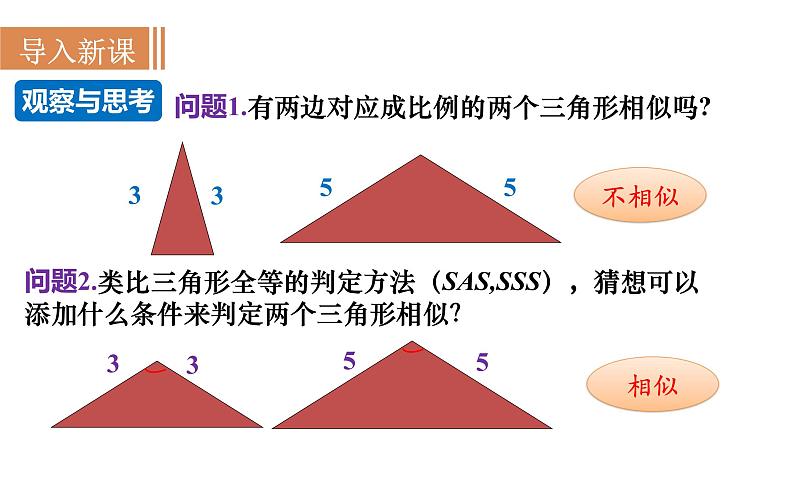
问题1.有两边对应成比例的两个三角形相似吗?
问题2.类比三角形全等的判定方法（SAS,SSS），猜想可以添加什么条件来判定两个三角形相似？
三角形相似的判定定理2的证明
证明：在△ABC的边AB上，截取AD＝A′B′，
过点D作BC的平行线DE交AC于E，
则∠ADE＝∠B，∠AED＝∠C，
∴△ADE∽△ABC.
∴△ADE≌△A′B′C′(SAS)，
∴△A′B′C′∽△ABC.
如果一个三角形的两条边与另一个三角形的两条边对应成比例，并且夹角相等，那么这两个三角形相似．(简称：两边成比例且夹角相等的两三角形相似．)
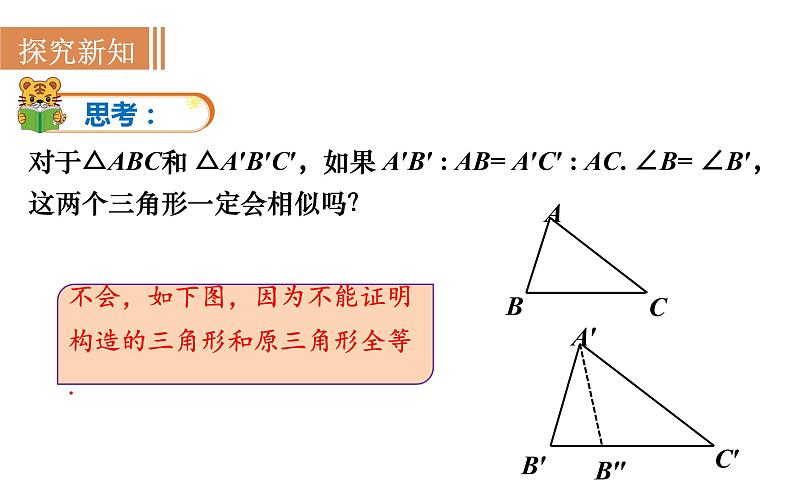
对于△ABC和 △A′B′C′，如果 A′B′ : AB= A′C′ : AC. ∠B= ∠B′，这两个三角形一定会相似吗？
不会，如下图，因为不能证明构造的三角形和原三角形全等.
如果两个三角形两边对应成比例，但相等的角不是两条对应边的夹角，那么两个三角形不一定相似，相等的角一定要是两条对应边的夹角.
又 ∠A′ = ∠A=45°，
(1)AB=5，AC=3 ，∠A=45°, A'B'=10, A'C'=6, ∠A=45°;
∴ △ABC ∽ △A′B′C′.
解：∵∠B=180°- ∠A-∠C=45°
∴∠B=∠B'=45°.
(2)∠A=38°，∠C=97°，∠A'=38°,∠B'=45° .
1. 在 △ABC 和 △DEF 中，∠C =∠F=70°，AC = 3.5 cm，BC = 2.5 cm，DF =2.1 cm，EF =1.5 cm.
证明：∵ AC = 3.5 cm，BC = 2.5 cm， DF = 2.1 cm，EF = 1.5 cm，
又 ∵∠C =∠F = 70°，
求证：△DEF∽△ABC.
∴ △DEF ∽△ABC.
2. 如图，△ABC 与 △ADE 都是等腰三角形，AD=AE，AB=AC，∠DAB=∠CAE. 求证：△ABC ∽△ADE.
证明：∵ △ABC 与 △ADE 是等腰三角形，
又 ∵∠DAB = ∠CAE，
∴ AD =AE，AB = AC，
∴ ∠DAB +∠BAE = ∠CAE +∠BAE，
即 ∠DAE =∠BAC，∴△ABC ∽ △ADE.
如图所示，△ABD∽△ACE.求证：△ADE∽△ABC.
证明：∵△ABD∽△ACE，
三角形相似的判定定理2的应用
∴∠BAD＋∠DAC＝∠CAE＋∠DAC，
∴△ABC∽△ADE.
即∠BAC＝∠DAE，
∠BAD＝∠CAE，
如图，AB⊥BC，CD⊥BC，AB＝2，CD＝3，BC＝7，在BC上找一点P，使以A、B、P为顶点的三角形和△CDP相似，并求BP的长．
∴设BP＝x，PC＝7－x，
如图，已知正方形ABCD中，P是BC上一点，且BP＝3PC，Q是CD的中点，求证：△ADQ∽△QCP.
【分析】欲证△ADQ∽△QCP，通过观察发现两个三角形已经具备一角对应相等，即∠D＝∠C，此时，可再寻求此对等角的两对邻边对应成比例．
证明：设正方形的边长为a.
又∵∠D＝∠C＝90°，
∵四边形ABCD为正方形，∴AD＝BC＝CD＝a.
∴△ADQ∽△QCP.
1．如图，在△ABC中，AB＝8，AC＝6，点D在AC上，且AD＝2，如果要在AB上找一点E，使△ADE与△ABC相似，则AE＝___________．
A．△ABD∽△ACE　　 B．△BOE∽△CODC．∠B＝∠C D．BE∶CD＝3∶2
3．如图，∠1＝∠2，添加一个条件____________，使得△ADE∽△ABC.
4．如图，在四边形ABCD中，AC、BD相交于点O，∠ABD＝∠ACD，试找出图中的相似三角形，________________________________．
△AOD∽△BOC，△AOB∽△DOC
5. 如图，D 是 △ABC 一边 BC 上一点，连接 AD，使 △ABC ∽ △DBA的条件是 ( ) A. AC : BC=AD : BD B. AC : BC=AB : AD C. AB2 = CD · BC D. AB2 = BD · BC
解析：当 △ADP ∽△ACB 时，AP : AB =AD : AC ，
6. 如图，已知 △ABC中，D 为边 AC 上一点，P 为边AB上一点，AB = 12，AC = 8，AD = 6，当 AP 的长度为 时，△ADP 和 △ABC 相似.
∴ AP : 12 =6 : 8 ，解得 AP = 9；
当 △ADP ∽△ABC 时，AD : AB =AP : AC ，
∴ 6 : 12 = AP : 8 ，解得 AP = 4.
∴ 当 AP 的长度为 4 或 9 时，△ADP 和 △ABC 相似．
∴ △ABC ∽ △DCA，
6. 如图，∠DAB =∠CAE，且 AB · AD = AE·AC，求证 △ABC ∽△AED.
又∵ ∠DAB =∠CAE，
∴∠ DAB +∠BAE =∠CAE +∠BAE ，
即∠DAE =∠BAC，
∴ △ABC ∽△AED.