初中数学沪科版九年级上册23.1 锐角的三角函数说课ppt课件

这是一份初中数学沪科版九年级上册23.1 锐角的三角函数说课ppt课件，共26页。PPT课件主要包含了方位角，北偏东，南偏东，东南方向，南偏西，北偏西，由ABAD－BD得，又AD＝AB＋BD，故AC＝AH－CH，在Rt△BCH中等内容，欢迎下载使用。
使学生会把实际问题转化为解直角三角形问题，从而会把实际问题转化为数学问题来解决．
善于将某些实际问题中的数量关系，归结为直角三角形元素之间的关系，从而利用所学知识把实际问题解决．
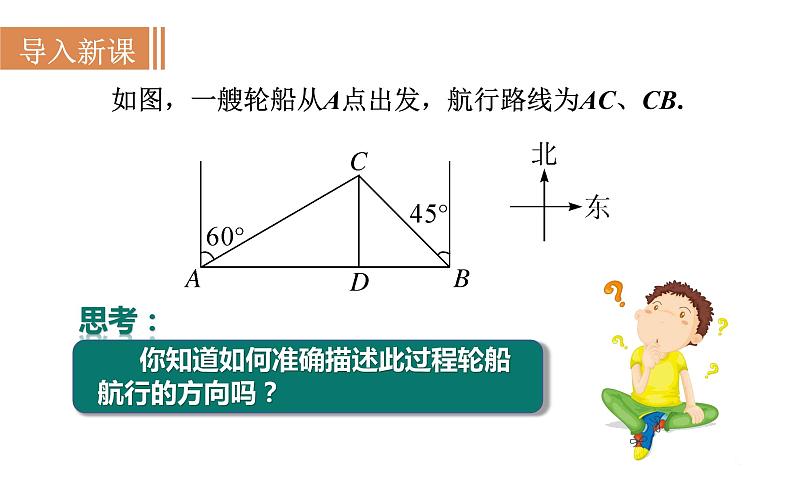
如图，一艘轮船从A点出发，航行路线为AC、CB.
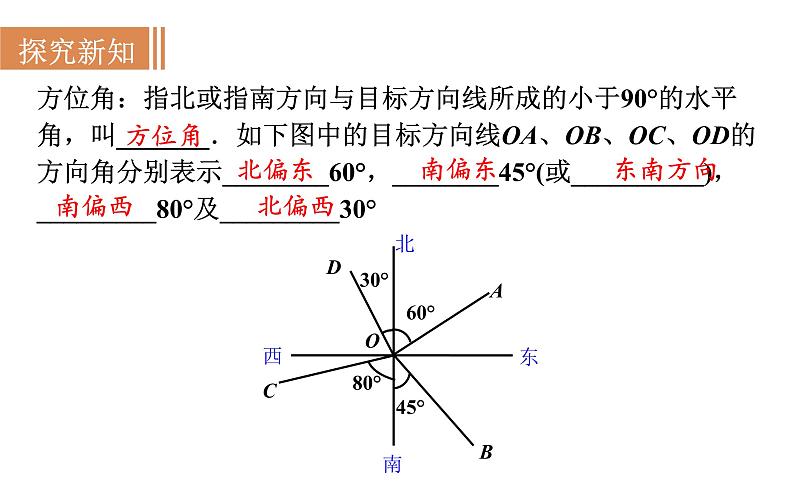
方位角：指北或指南方向与目标方向线所成的小于90°的水平角，叫_______．如下图中的目标方向线OA、OB、OC、OD的方向角分别表示________60°，________45°(或__________)，_________80°及_________30°
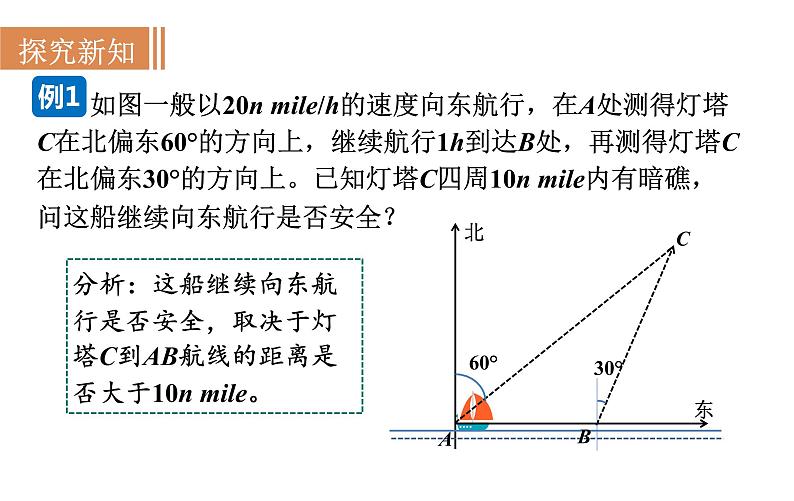
如图一般以20n mile/h的速度向东航行，在A处测得灯塔C在北偏东60°的方向上，继续航行1h到达B处，再测得灯塔C在北偏东30°的方向上。已知灯塔C四周10n mile内有暗礁，问这船继续向东航行是否安全？
分析：这船继续向东航行是否安全，取决于灯塔C到AB航线的距离是否大于10n mile。
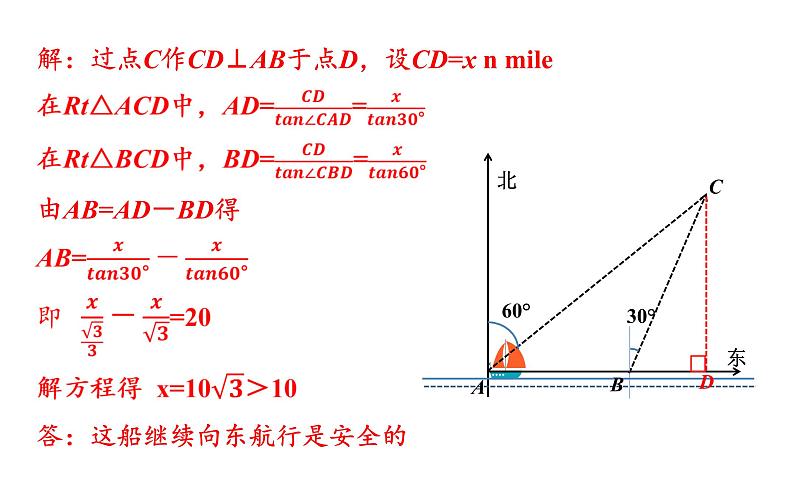
答：这船继续向东航行是安全的
解：过点C作CD⊥AB于点D，设CD=x n mile
如图所示，某货船以24海里/时的速度将一批重要物资从A处运往正东方向的M处，在点A处测得某岛C在北偏东60°的方向上．该货船航行30分钟后到达B处，此时又测得该岛在北偏东30°方向上，已知在岛C周围9海里的区域内有暗礁，若继续向正东方向航行，该货船有无触礁危险？试说明理由．
∴若继续向正东方向航行，该货船没有触礁危险．
解：过C作CD⊥AB于点D.
∠CAB＝90°－60°＝30°，
∠CBD＝90°－30°＝60°.
解：过B作BH⊥AC交AC延长线于H.
在Rt△ABH中，∠BAH＝79.8°－53.2°＝26.6°，
∴AH＝2BH.由BH2＋AH2＝AB2＝202
如图，一艘海轮位于灯塔P的北偏东65°方向，距离灯塔80海里的A处，它沿正南方向航行一段时间后，到达位于灯塔P的南偏东34°方向上的B处．这时海轮所在的B处距离灯塔P有多远(精确到0.01海里)?
因此，当海轮到达位于灯塔P的南偏东34°方向时，它距离灯塔P大约129.66海里．
解：如图，在Rt△APC中，
PC＝PA·cs(90°－65°)＝80×cs25°≈72.505.
在Rt△BPC中，∠B＝34°，
答：计划修筑的这条高速公路不会穿越保护区．
解：过点P作PC⊥AB，C是垂足．
则∠APC＝30°，∠BPC＝45°，
AC＝PC·tan30°，BC＝PC·tan45°.
∴PC · tan30°＋PC · tan45°＝200，
解得 PC≈126.8km＞100km.
利用解直角三角形的知识解决实际问题的一般过程是：
将实际问题抽象为数学问题（画出平面图形，转化为解直角三角形的问题）；
根据条件的特点，适当选用锐角三角形函数等去解直角三角形；
一条东西走向的高速公路上有两个加油站A，B，在A的北偏东45°方向还有一个加油站C，C到高速公路的最短距离是30km，B，C间的距离是60km，想要经过C修一条笔直的公路与高速公路相交，使两路交叉口P到B，C的距离相等，请求出交叉口P到加油站A的距离(结果保留根号)．
分析：此题针对点P的位置分两种情况讨论，即点P可能在线段AB上，也可能在BA的延长线上．
(1)如图①，在Rt△BDC中，
CD＝30km，BC＝60km，
∴AD＝DC＝30km.
在Rt△ADC中，∵∠A＝45°，
(2)如图②，同理可求得
∴∠BCP＝∠B＝30°.
∠CPD＝∠B＋∠BCP＝60°.
解直角三角形的关键是找到与已知和未知相关联的直角三角形，当图形中没有直角三角形时，要通过作辅助线构筑直角三角形（作某边上的高是常用的辅助线）；当问题以一个实际问题的形式给出时，要善于读懂题意，把实际问题化归为直角三角形中的边角关系.
1.如图，小红从A地向北偏东30°方向走100m到B地，再从B地向西走200m到C地，这时小红距A地(　　)
2.如右图，C、D是两个村庄，分别位于一个湖的南、北两端A和B的正东方向上，且D位于C的北偏东30°方向上，CD＝6km，则AB＝_________km.
3.如图，一艘船向正北航行，在A处看到灯塔S在船的北偏东30°的方向上，航行12海里到达B处，在B处看到灯塔S在船的北偏东60°的方向上，此船继续沿正北方向航行过程中，距灯塔S的最近距离是______海里．
4. 如图，一架飞机从A地飞往B地，两地相距600km.飞行员为了避开某一区域的雷雨云层，从机场起飞以后，就沿与原来的飞行方向成30°角的方向飞行，飞行到中途，再沿与原来的飞行方向成45°角的方向继续飞行直到终点．这样飞机的飞行路程比原来的路程600km远了多少？
解：过点C作CD⊥AB于点D，
747－600＝147(km)
答：飞机的飞行路程比原来的路程600km远了147km.
分析： 在Rt△CDB中，利用三角函数即可求得BC，BD的长，则可求得甲、乙所用的时间，比较二者之间的大小即可．
解：由题意得∠BCD=55°，∠BDC=90°
∴BD=CD·tan∠BCD=40×tan55°≈57.2（米）