人教A版 (2019)选择性必修 第二册5.3 导数在研究函数中的应用教案设计

这是一份人教A版 (2019)选择性必修 第二册5.3 导数在研究函数中的应用教案设计，共19页。教案主要包含了重点小结，基础自测，方法归纳，跟踪训练1，跟踪训练2，变式训练，跟踪训练3，易错辨析等内容，欢迎下载使用。

5.3.1.1函数的单调性与导数

要点　导数与函数的单调性
在某个区间(a，b)内，函数的单调性与其导函数的正负有如下关系：
导数
函数的单调性
f′(x)>0
单调递增
f′(x)<0
单调递减
f′(x)＝0
常数函数
【重点小结】
(1)若在某区间上有有限个点使f ′(x)＝0，其余的点恒有f ′(x)>0，则f(x)仍为增函数(减函数的情形完全类似)．
(2)f(x)为增函数的充要条件是对任意的x∈(a，b)都有f ′(x)≥0且在(a，b)内的任一非空子区间上f ′(x)不恒为0.
【基础自测】
1．判断正误(正确的画“√”，错误的画“×”)
(1)函数f(x)在定义域上都有f′(x)<0，则函数f(x)在定义域上单调递减．(　　)
(2)函数在某一点的导数越大，函数在该点处的切线越“陡峭”．(　　)
(3)函数在某个区间上变化越快，函数在这个区间上导数的绝对值越大．(　　)
(4)判断函数单调性时，在区间内的个别点f′(x)＝0，不影响函数在此区间的单调性．(　　)
【答案】（1）×（2）×（3）√（4）√
2．函数y＝f(x)的图象如图所示，则(　　)
A．f′(3)>0
B．f′(3)<0
C．f′(3)＝0
D．f′(3)的符号不确定
【答案】B
【解析】由图象可知，函数f(x)在(1,5)上单调递减，则在(1,5)上有f′(x)<0，所以f′(3)<0.
3．导函数y＝f′(x)的图象如图所示，则函数y＝f(x)的图象可能是(　　)


【答案】D
【解析】∵当x>0时，f′(x)>0，当x<0时，f′(x)<0，∴函数f(x)在(0，＋∞)上是增函数，在(－∞，0)上是减函数，故选D.
4．命题甲：对任意x∈(a，b)，有f′(x)>0；命题乙：f(x)在(a，b)内是单调递增的，则甲是乙的(　　)
A．充分不必要条件 B．必要不充分条件
C．充要条件 D．既不充分也不必要条件
【答案】A
【解析】例如取f(x)＝x3(－1

题型一　导函数与原函数图象间的关系
【例1】(1)设函数f(x)在定义域内可导，f(x)的图象如图所示，则导函数f′(x)的图象可能为(　　)

【答案】(1)D　
【解析】(1)由f(x)的图象可知，y＝f(x)在(－∞，0)上是增函数，因此在x<0时，有f′(x)>0(即全部在x轴上方)，故排除A、C.从原函数图象上可以看出，在区间(0，x1)上原函数是增函数，f′(x)>0；在区间(x1，x2)上原函数是减函数，f′(x)<0；在区间(x2，＋∞)上原函数是增函数，f′(x)>0，故排除B，故选D.
(2)(多选题)设f′(x)是函数f(x)的导函数，将y＝f(x)和y＝f′(x)的图象画在同一个平面直角坐标系中，正确的是(　　)

【答案】(2)ABC
【解析】(2)A，B，C均有可能；对于D，若C1为导函数，则y＝f(x)应为增函数，不符合；若C2为导函数，则y＝f(x)应为减函数，也不符合，D不可能，故选ABC.
【方法归纳】
函数与导数图象间的关系
判断函数与导数图象间的对应关系时，首先要弄清所给图象是原函数的图象还是导函数的图象，其次再注意以下两个方面：
(1)函数的单调性与其导函数的正负的关系：在某个区间(a，b)内，若f′(x)>0，则y＝f(x)在(a，b)上单调递增；如果f′(x)<0，则y＝f(x)在这个区间上单调递减；若恒有f′(x)＝0，则y＝f(x)是常数函数，不具有单调性．
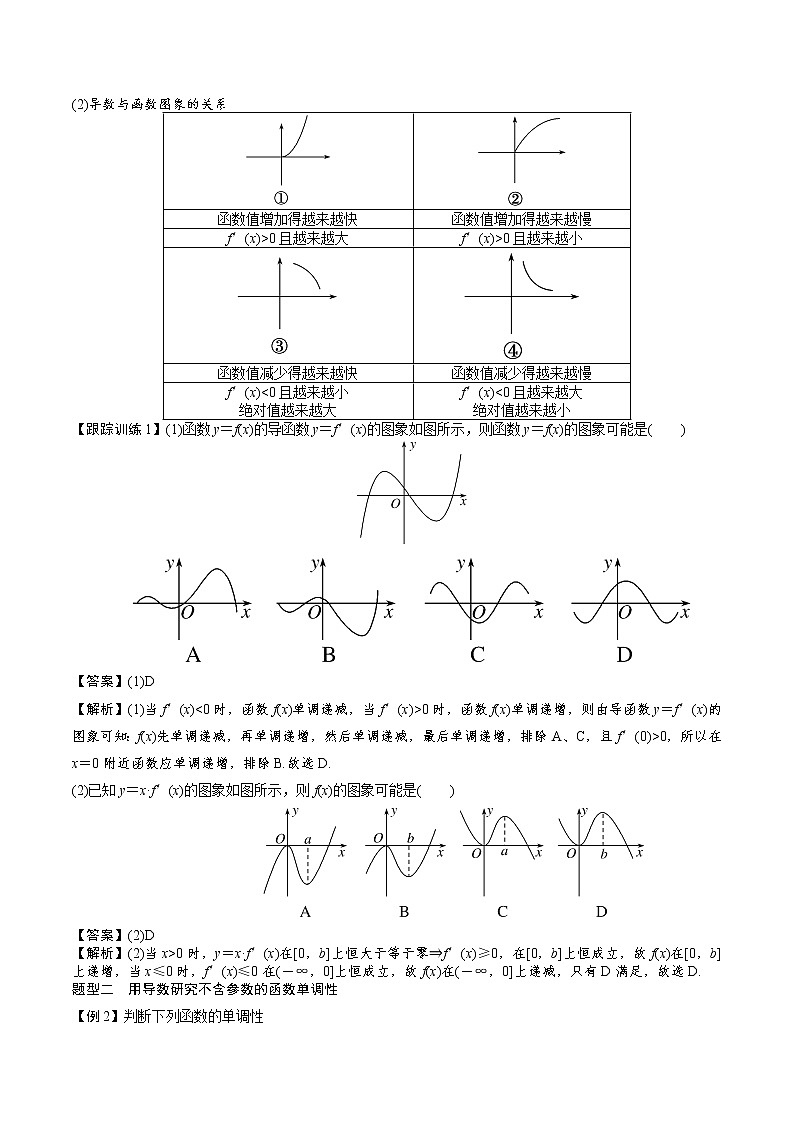
(2)导数与函数图象的关系


函数值增加得越来越快
函数值增加得越来越慢
f′(x)>0且越来越大
f′(x)>0且越来越小


函数值减少得越来越快
函数值减少得越来越慢
f′(x)<0且越来越小
绝对值越来越大
f′(x)<0且越来越大
绝对值越来越小
【跟踪训练1】(1)函数y＝f(x)的导函数y＝f′(x)的图象如图所示，则函数y＝f(x)的图象可能是(　　)


【答案】(1)D　
【解析】(1)当f′(x)<0时，函数f(x)单调递减，当f′(x)>0时，函数f(x)单调递增，则由导函数y＝f′(x)的图象可知：f(x)先单调递减，再单调递增，然后单调递减，最后单调递增，排除A、C，且f′(0)>0，所以在x＝0附近函数应单调递增，排除B.故选D.
(2)已知y＝x·f′(x)的图象如图所示，则f(x)的图象可能是(　　)

【答案】(2)D
【解析】(2)当x>0时，y＝x·f′(x)在[0，b]上恒大于等于零⇒f′(x)≥0，在[0，b]上恒成立，故f(x)在[0，b]上递增，当x≤0时，f′(x)≤0在(－∞，0]上恒成立，故f(x)在(－∞，0]上递减，只有D满足，故选D.
题型二　用导数研究不含参数的函数单调性
【例2】判断下列函数的单调性
(1)f(x)＝x2－ln x；
(2)f(x)＝
(3)f(x)＝x3＋.
【解析】(1)函数f(x)的定义域为(0，＋∞)
f′(x)＝2x－＝
因为x>0，所以x＋1>0
令f′(x)>0，解得x>
所以函数f(x)在(，＋∞)上单调递增，
令f′(x)<0，解得0 所以函数f(x)在(0，)上单调递减．
(2)函数f(x)的定义域为(－∞，2)∪(2，＋∞)
f′(x)＝＝
因为x∈(－∞，2)∪(2，＋∞)，所以ex>0，(x－2)2>0
令f′(x)>0，得x>3，所以函数f(x)在(3，＋∞)上单调递增；
令f′(x)<0，得x<3，又x∈(－∞，2)∪(2，＋∞)
所以函数f(x)在(－∞，2)和(2,3)上单调递减．
(3)函数f(x)的定义域为(－∞，0)∪(0，＋∞)
f′(x)＝3x2－＝3(x2－)
令f′(x)>0，得x<－1或x>1，
所以函数f(x)在(－∞，－1)和(1，＋∞)上单调递增；
令f′(x)<0得－1 所以函数f(x)在(－1,0)和(0,1)上单调递减．
【方法归纳】
用导数判断函数单调性的步骤
(1)确定函数f(x)的定义域；
(2)求导函数f′(x)；
(3)解不等式f′(x)>0(或f′(x)<0)；
(4)写出结论．
【跟踪训练2】(1)已知函数f(x)＝xln x，x∈(0,5)，下列判断正确的是(　　)
A．在(0,5)上是增函数
B．在(0,5)上是减函数
C．在(0，)上是减函数，在(，5)上是增函数
D．在(0，)上是增函数，在(，5)上是减函数
【答案】(1)C　
【解析】(1)由f(x)＝xln x，可得f′(x)＝ln x＋x·＝ln x＋1.由f′(x)>0且x∈(0,5)，可得 (2)函数f(x)＝sin x－x在(0，π)上单调________．(填“递增”、“递减”)．
【答案】(2)递减
【解析】(2)因为f(x)＝sin x－x，x∈(0，π)
所以f′(x)＝cos x－1<0.
所以函数f(x)＝sin x－x在(0，π)上单调递减．
题型三　用导数研究含参函数的单调性
【例3】已知函数f(x)＝ax2－(a＋1)x＋lnx，a>0，试讨论函数f(x)的单调性．
【解析】函数的定义域为(0，＋∞),
f′(x)＝ax－(a＋1)＋＝＝，
①当01，
∴x∈(0,1)和(，＋∞)时，f′(x)>0；
x∈时，f′(x)<0，
∴函数f(x)在(0,1)和上单调递增，在上单调递减；
②当a＝1时，＝1，∴f′(x)≥0在(0，＋∞)上恒成立，
∴函数f(x)在(0，＋∞)上单调递增；
③当a>1时，0<<1，∴x∈(0，)和(1，＋∞)时，f′(x)>0；
x∈)时，f′(x)<0，
∴函数f(x)在和(1，＋∞)上单调递增，在上单调递减，综上，当0 当a＝1时，函数f(x)在(0，＋∞)上单调递增；
当a>1时，函数f(x)在和(1，＋∞)上单调递增，在上单调递减．
【变式训练】本例中的条件“a>0”改为“a∈R”，结果如何？
【解析】a>0时，讨论同上；当a≤0时，ax－1<0，
∴x∈(0,1)时，f′(x)>0，x∈(1，＋∞)时，f′(x)<0，
∴函数f(x)在(0,1)上单调递增，在(1，＋∞)上单调递减，
综上，当a≤0时，函数f(x)在(0,1)上单调递增，在(1，＋∞)上单调递减；当0 当a>1时，函数f(x)在和(1，＋∞)上单调递增，在上单调递减．
【方法归纳】
在讨论含有参数的函数单调性时，若f′(x)中的参数不容易判断其正负时，需要对参数进行分类，分类的标准：
(1)按导函数是否有零点分大类；
(2)在大类中再按导数零点的大小分小类；
(3)在小类中再按零点是否在定义域中分类．
【跟踪训练3】已知函数f(x)＝ex(ex－a)－a2x，讨论f(x)的单调性．
【解析】函数f(x)的定义域为(－∞，＋∞)，
f′(x)＝ex(ex－a)＋ex·ex－a2＝2e2x－aex－a2
＝(2ex＋a)(ex－a)．
①若a＝0，则f(x)＝e2x，在(－∞，＋∞)上单调递增．
②若a>0，则由f′(x)＝0得x＝ln a.
当x∈(－∞，ln a)时，f′(x)<0；
当x∈(ln a，＋∞)时，f′(x)>0.
故f(x)在(－∞，ln a)上单调递减，
在(ln a，＋∞)上单调递增．
③若a<0，则由f′(x)＝0得x＝ln .
当x∈时，f′(x)<0；
当x∈时，f′(x)>0.
故f(x)在上单调递减，
在上单调递增．
【易错辨析】讨论函数单调性时忽略定义域致错
【例4】已知函数f(x)＝，判断函数f(x)的单调性．
【解析】函数f(x)的定义域为(0,1)∪(1，＋∞)，
f′(x)＝.
由f′(x)＝0，可得x＝e.
则当0 f′(x)<0，f(x)为减函数；
当x>e时，f′(x)>0，f(x)为增函数．

一、单选题
1．已知是定义在上的函数，那么“在上单调递减”是“存在，使得”的（ ）
A．充分不必要条件 B．必要不充分条件
C．充分必要条件 D．既不充分也不必要条件
【答案】A
【分析】
根据函数的单调性和导数的关系即可判断充分条件成立，通过举反例可以证明必要条件不成立，由此即可得到结果.
【解析】
因为在上单调递减，所以在上恒成立，故存在，使得成立；
反之，若，则，存在，使得，而在上既不是增函数也不是减函数；所以 是定义在上的函数，那么“在上单调递减”是“存在，使得”的充分不必要条件.
故选：A.
2．设函数在上单调递减，则实数的取值范围是（ ）
A． B． C． D．
【答案】B
【分析】
根据题意，容易判断在上恒成立，进而分离参数转化为最值问题，最后求出答案.
【解析】
由题意，在上恒成立，则在上恒成立，因为，所以.
故选：B.
3．设函数在上存在导数，对任意的有，若，则的取值范围是（ ）
A． B． C． D．
【答案】B
【分析】
构造函数，可得在上单调递增，进而求解不等式即可.
【解析】
由题意，，构造函数，
则，得在上单调递增，
由，
得，即，
根据函数在上单调递增，可得，解得.
所以的取值范围是
故选：B
4．函数的图象大致为（ ）
A．
B．

C．
D．

【答案】D
【分析】
先判断函数为偶函数，再根据导数判断出函数的单调性后可得正确的选项.
【解析】
的定义域为，
而，故为偶函数，故排除AC，
当时，，则，
设，，
则，故在上为增函数，
而，故在上存在一个零点，
且，
当时，；当时，，
故在上为减函数，在上为增函数，
故选：D.
5．函数，若满足恒成立，则实数的取值范围为（ ）
A． B． C． D．
【答案】C
【解析】
∵，且，
∴函数为单调递增的奇函数．
于是，可以变为，
即，∴，而，可知实数，
故实数的取值范围为．
故选：C.
6．已知定义在上的可导函数，对任意的实数x，都有，且当时，恒成立，若不等式恒成立，则实数的取值范围是（ ）
A． B． C． D．
【答案】D
【分析】
由题意可得，令，根据奇偶性的定义，可得为偶函数，利用导数可得的单调性，将题干条件化简可得，即，根据的单调性和奇偶性，计算求解，即可得答案.
【解析】
由，得，
记，则有，即为偶函数，
又当时，恒成立，
所以在上单调递增，
所以由，得，
即，
所以，即，解得，
故选：D.
7．下列函数中，既满足图象关于原点对称，又在上单调递增的是（ ）
A． B．
C． D．
【答案】C
【分析】
根据函数的奇偶性和导函数，逐项分析各函数即可得出答案.
【解析】
选项A中，在 上不恒非负，选项A错误；
选项B中， ，所以 的图像不关于原点对称，选项B错误；
选项C中， ，即 为奇函数，图像关于原点对称
又，时，恒成立
所以在上单调递增，选项C正确；
选项D中，当 时，在上为单调增函数在 上为单调减函数，选项D错误.
故选：C.
8．已知函数若存在三个不相等的实数，，，使得，则实数的取值范围是（ ）
A． B． C． D．
【答案】B
【分析】
构造函数，求导后判断其在上单调递增，在上单调递减，从而做出图像分析交点情况可得出答案.
【解析】
解：


当时，，单调递增；
当时，，单调递减；
故当时，函数取得最大值1，由此可作出的图像.
存在三个不相等的实数，，，使得等价于一条垂直于轴的直线，与的图像有三个不同的交点.
当时，如图，最多有两个交点，不符合题意；

当时，如图，存在三个交点，符合题意；

当时，如图，最多有两个交点，不符合题意.

所以的取值范围.
故选：B

二、多选题
9．若，则下列结论一定正确的是（ ）
A． B．
C． D．
【答案】BC
【分析】
对选项A，利用作差法比较即可判断A错误，对选项B，首先构造，再根据的单调性即可判断B正确，对选项C，根据，，即可判断C正确，对选项D，利用特殊值即可判断D错误.
【解析】
因为，所以，即.
对选项A，，因为，所以，
即，故A错误.
对选项B，设，，
因为时，，所以为增函数，
因为，所以，即，故B正确.
对选项C，因为，所以，
又因为，所以，故C正确.
对选项D，因为，当，时，，
故D错误.
故选：BC
10．如果函数在区间上是增函数，且在区间是减函数，那么称函数是区间上的“缓增函数”，区间叫做“缓增区间”.则下列函数是区间上的“缓增函数”的是（ ）
A． B．
C． D．
【答案】CD
【分析】
根据题意依次判断选项中函数和在区间上的单调性即可得到答案.
【解析】
对选项A，在单调递增，
设，，
，，为增函数，故A错误；
对选项B，在单调递增，
设，，
，，为增函数，故B错误；
对选项C，在单调递增，
设，，
，，为减函数，故C正确；
对选项D，在单调递增，
设，，
，，为减函数，故D正确.
故选：CD
11．已知函数，则下列有关的叙述正确的是（ ）
A．在处的切线方程为 B．在上是单调递减函数
C．是极大值点 D．在上的最小值为0
【答案】ACD
【分析】
求出导函数，利用导数的几何意义可判断A；利用导数与函数单调性之间的关系可判断B；利用极大值点的定义可判断C；利用极值以端点值可判断D.
【解析】
，，
A，，，
所以函数在处的切线方程为，即，A正确；
B，，当时，则，
，，所以函数在上是单调递增函数，B错误；
C，，当时，，；
当时，，；
所以函数在上单调递增；在上单调递减；
所以是极大值点，C正确；
D， 由B、C可知，当时， ，函数单调递增；
当时，，函数单调递减；
，.
所以函数在上的最小值为0，D正确.
故选：ACD

第II卷（非选择题）
请点击修改第II卷的文字说明

三、填空题
12．已知函数在上存在单调递增区间，则的取值范围是______．
【答案】
【分析】
由在上存在单调递增区间，在有解，则求解即可．
【解析】
因为在上存在单调递增区间，
所以在有解，
令，则，
得
故答案为：.
13．已知函数在上单调递增，则实数的取值范围________.
【答案】
【分析】
首先求导，根据题意得到，恒成立，再利用导数求解最值即可得到答案.
【解析】
，，
因为函数在上单调递增，
所以，恒成立，
即，恒成立，
设，
，
，，为减函数，
，，为增函数，
所以，即.
故答案为：
14．若函数在区间上具有单调性，则a的取值范围是________．
【答案】
【分析】
对函数求导，将函数在区间上具有单调性，转化为在区间恒大于0，或恒小于0，进而求出a的取值范围
【解析】
，函数在区间上具有单调性等价于或在上恒成立，
则或，设，
当时，取得最大值，，当时，取得最小值，
所以或．
故答案为：

四、解答题
15．已知函数（）．
（1）讨论的单调区间；
（2）求在上的最大值．
【答案】
（1）答案见解析
（2）
【分析】
（1）直接求导，根据的取值范围分情况讨论；
（2）分情况讨论函数在的单调性及最值情况.
（1）
解：定义域，
①，在上单减；
②，在上单增，单减；
（2）
解：由（1）知：①时，在单减，；
②时，在单增，；
③时，在单增，单减，；
综合.
16．已知函数.若函数在定义域上单调递增，求实数的取值范围.
【答案】.
【分析】
对函数求导得，利用给定单调性列出恒成立的不等式即可推理作答.
【解析】
定义域为，
由得，
因函数在定义域上单调递增，
于是得在恒成立，
即在恒成立，
而，
当且仅当，即时取“=”，则，
所以实数a的取值范围是.
17．设函数，其中常数.若函数在上是增函数，求实数a的取值范围.
【答案】.
【分析】
由已知结合导数与单调性的关系可将问题转化为在上恒成立，分离参数后转化为求解函数的最值，然后构造函数即可求解.
【解析】
因为函数在上是增函数，
所以在上恒成立，
即在上恒成立，
设函数，则，
当时，，当时，，
所以函数在上单调递减，在上单调递增，
则，所以，解得.