浙教版初中数学九年级上册期末测试卷（困难）（含答案解析）

这是一份浙教版初中数学九年级上册期末测试卷（困难）（含答案解析），共32页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

浙教版初中数学九年级上册期末测试卷
考试范围：全册；考试时间：120分钟；总分：120分
学校:___________姓名：___________班级：___________考号：___________
第I卷（选择题）

一、选择题（本大题共12小题，共36.0分。在每小题列出的选项中，选出符合题目的一项）
1. 若数a使关于x的分式方程1x−3+x+a3−x=1有非负整数解，且使关于x的二次函数y=4x2+a+6x−a−3其对称轴在y轴左侧，则符合条件的所有整数a的和是(    )
A. −5 B. −3 C. 0 D. 2
2. 对于二次函数y=ax2+12−2axa<0，下列说法正确的个数是(    )
①对于任何满足条件的a，该二次函数的图象都经过点(2,1)和(0,0)两点．
②若该函数图象的对称轴为直线x=x0，则必有1 ③当x≥0时，y随x的增大而增大．
④若P(4,y1)，Q(4+m,y2)(m>0)是函数图象上的两点，如果y1>y2总成立，则a≤−112．
A. 1个 B. 2个 C. 3个 D. 4个
3. 从一副扑克牌(去掉大王和小王)中，任意抽出一张，恰好是红桃的概率是(    )
A. 1354 B. 14 C. 1 D. 113
4. 将五张分别画有等边三角形、平行四边形、矩形、等腰梯形、正六边形的卡片任意摆放，将有图形的一面朝下，从中任意翻开一张卡片，图形一定是中心对称图形的概率是(    )
A. 15 B. 25 C. 35 D. 45
5. 下列说法正确的是(    )
A. 掷一枚均匀的骰子，骰子停止转动后，6点朝上是必然事件
B. 甲、乙两人在相同条件下各射击10次，他们的成绩平均数相同，方差分别是，，则甲的射击成绩较稳定
C. “明天降雨的概率为12”，表示明天有半天都在降雨
D. 了解一批电视机的使用寿命，适合用普查的方式
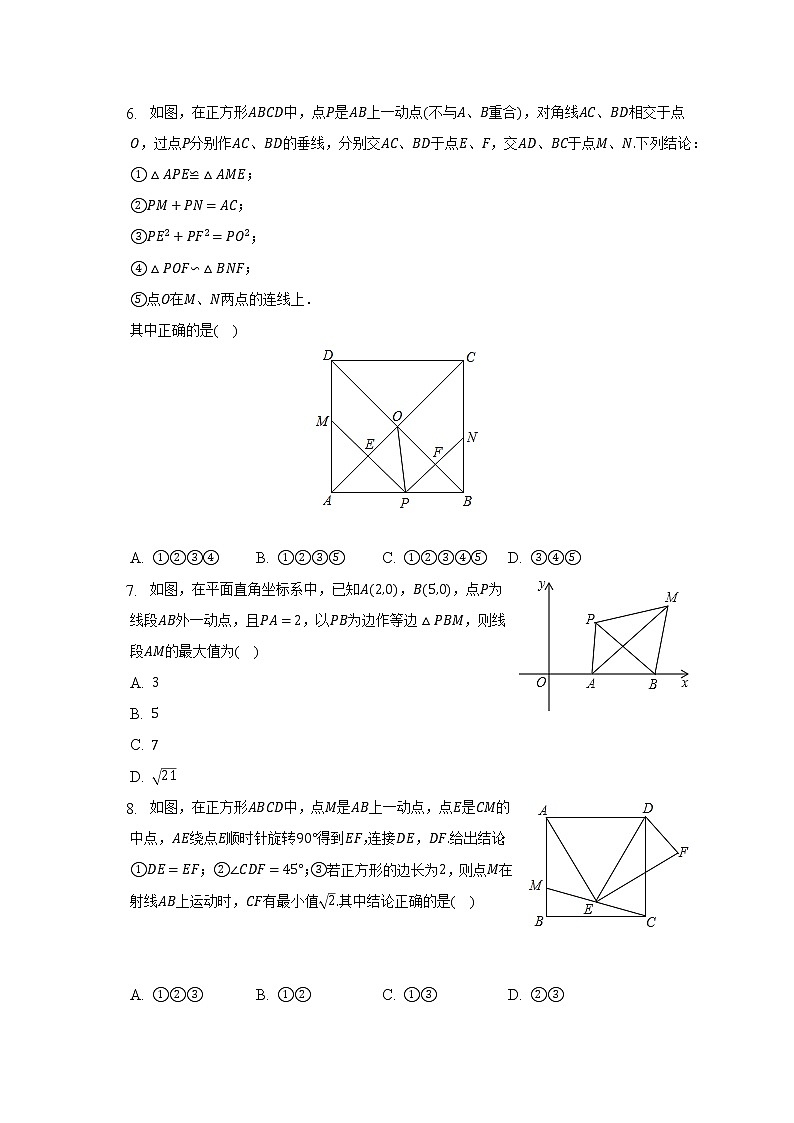
6. 如图，在正方形ABCD中，点P是AB上一动点(不与A、B重合)，对角线AC、BD相交于点O，过点P分别作AC、BD的垂线，分别交AC、BD于点E、F，交AD、BC于点M、N.下列结论：
①△APE≌△AME；
②PM+PN=AC；
③PE2+PF2=PO2；
④△POF∽△BNF；
⑤点O在M、N两点的连线上．
其中正确的是(    )

A. ①②③④ B. ①②③⑤ C. ①②③④⑤ D. ③④⑤
7. 如图，在平面直角坐标系中，已知A(2,0)，B(5,0)，点P为线段AB外一动点，且PA=2，以PB为边作等边△PBM，则线段AM的最大值为(    )
A. 3
B. 5
C. 7
D. 21
8. 如图，在正方形ABCD中，点M是AB上一动点，点E是CM的中点，AE绕点E顺时针旋转90°得到EF，连接DE，DF.给出结论：①DE=EF；②∠CDF=45°；③若正方形的边长为2，则点M在射线AB上运动时，CF有最小值2.其中结论正确的是(    )


A. ①②③ B. ①② C. ①③ D. ②③
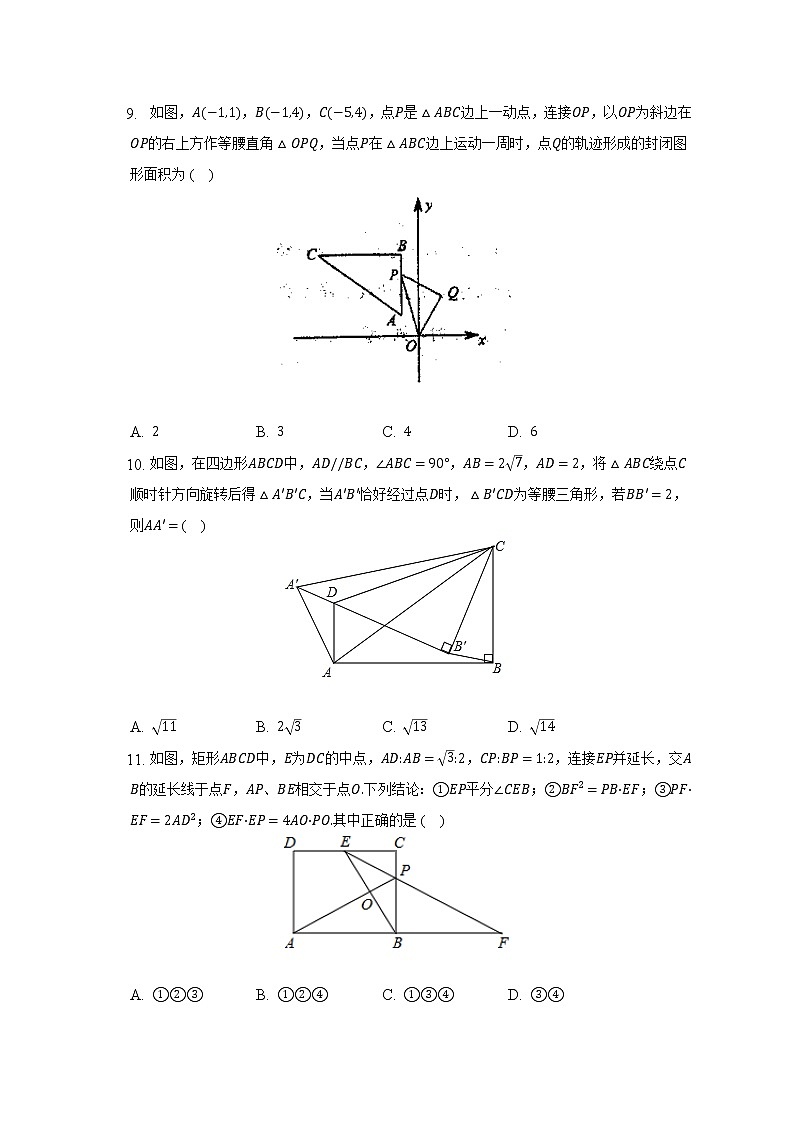
9. 如图，A−1,1，B−1,4，C−5,4，点P是△ABC边上一动点，连接OP，以OP为斜边在OP的右上方作等腰直角△OPQ，当点P在△ABC边上运动一周时，点Q的轨迹形成的封闭图形面积为(    )

A. 2 B. 3 C. 4 D. 6
10. 如图，在四边形ABCD中，AD//BC，∠ABC=90°，AB=27，AD=2，将△ABC绕点C顺时针方向旋转后得△A′B′C，当A′B′恰好经过点D时，△B′CD为等腰三角形，若BB′=2，则AA′=(    )

A. 11 B. 23 C. 13 D. 14
11. 如图，矩形ABCD中，E为DC的中点，AD:AB=3:2，CP:BP=1:2，连接EP并延长，交AB的延长线于点F，AP、BE相交于点O.下列结论：①EP平分∠CEB；②BF2=PB·EF；③PF·EF=2AD2；④EF·EP=4AO·PO.其中正确的是(    )

A. ①②③ B. ①②④ C. ①③④ D. ③④
12. 如图，点A在线段BD上，在BD的同侧作等腰直角三角形ABC和等腰直角三角形ADE，CD与BE、AE分别交于点P、M.下列结论：
 ①△BAE∽△CAD;
 ②MP⋅MD=MA⋅ME;
 ③2CB2=CP⋅CM．
其中正确的是(    )

A.  ① ② ③ B.  ① C.  ① ② D.  ② ③
第II卷（非选择题）

二、填空题（本大题共4小题，共12.0分）
13. 将抛物线y=x2向左平移4个单位，再向上平移6个单位，所得的抛物线的解析式为__________．
14. 有4根细木棒，长度分别为2cm，3cm，4cm，5cm，从中任选3根，恰好能搭成一个三角形的概率          ．
15. 如图，将半径为2cm的圆形纸片折叠后，圆弧恰好经过圆心O，则折痕AB的长为________________________cm．


16. 如图，在河对岸有一矩形场地ABCD，为了估测场地大小，在笔直的河岸l上依次取点E，F，N，使AE⊥l，BF⊥l，点N，A，B在同一直线上．在F点观测A点后，沿FN方向走到M点，观测C点发现∠1=∠2.测得EF=15米，FM=2米，MN=8米，∠ANE=45°，则场地的边AB为______米，BC为______米．




三、解答题（本大题共9小题，共72.0分。解答应写出文字说明，证明过程或演算步骤）
17. (本小题8.0分)
如图，二次函数y=x2+bx+c的图象与x轴交于A，B两点，与y轴交于点C，且关于直线x=1对称，点A的坐标为(−1,0)．
(1)求二次函数的表达式；
(2)当y<0时，写出x的取值范围；
(3)当a≤x≤a+1时，二次函数y=x2+bx+c的最小值为2a，求a的值．

18. (本小题8.0分)
在直角坐标系中，设函数y=ax2+bx+1(a,b是常数，a≠0)．
(1)若该函数的图象经过(1,0)和(2,1)两点，求函数的表达式，并写出函数图象的顶点坐标；
(2)已知a=b=1，当x=p，q(p,q是实数，p≠q)时，该函数对应的函数值分别为P，Q.若p+q=2，求证：P+Q>6．
19. (本小题8.0分)
如图，可以自由转动的转盘被它的两条直径分成了四个分别标有数字的扇形区域，其中标有数字“1”的扇形的圆心角为120°.转动转盘，待转盘自动停止后，指针指向一个扇形的内部，则该扇形内的数字即为转出的数字，此时，称为转动转盘一次(若指针指向两个扇形的交线，则不计转动的次数，重新转动转盘，直到指针指向一个扇形的内部为止)．
(1)转动转盘一次，求转出的数字是−2的概率；
(2)转动转盘两次，用树状图或列表法求这两次分别转出的数字之积为正数的概率．

20. (本小题8.0分)
小军与小玲共同发明了一种“字母棋”，进行比胜负的游戏．她们用四种字母做成10只棋子，其中A棋1只，B棋2只，C棋3只，D棋4只．

“字母棋”的游戏规则为：
①游戏时两人各摸一只棋进行比赛称一轮比赛，先摸者摸出的棋不放回；
②A棋胜B棋、C棋；B棋胜C棋、D棋；C棋胜D棋；D棋胜A棋；
③相同棋子不分胜负．
(1)若小玲先摸，问小玲摸到C棋的概率是多少？
(2)已知小玲先摸到了C棋，小军在剩余的9只棋中随机摸一只，问这一轮中小玲胜小军的概率是多少？
(3)已知小玲先摸一只棋，小军在剩余的9只棋中随机摸一只，问这一轮中小玲希望摸到哪种棋胜小军的概率最大？
21. (本小题8.0分)
综合与实践
问题情境：
如图①，点E为正方形ABCD内一点，∠AEB=90°，将Rt△ABE绕点B按顺时针方向旋转90°，得到△CBE′(点A的对应点为点C).延长AE交CE′于点F，连接DE．
猜想证明：
(1)试判断四边形BE′FE的形状，并说明理由；
(2)如图②，若DA=DE，请猜想线段CF与FE′的数量关系并加以证明；
解决问题：
(3)如图①，若AB=15，CF=3，请直接写出DE的长．


22. (本小题8.0分)
已知在Rt△ABC中，AB=BC，在Rt△ADE中，AD=DE，连接EC，取EC的中点M，连接DM，BM．

(1)若点D在边AC上，点E在边AB上且与点B不重合，如图1，求证：BM=DM且BM⊥DM．
(2)△ADE绕点A逆时针旋转小于45∘的角，如图2，那么(1)中的结论是否仍然成立?如果不成立，请举出反例;如果成立，请给予证明．
23. (本小题8.0分)
如图，OA=OB，AB交⊙O于点C、D，AC与BD是否相等？为什么？

24. (本小题8.0分)
等边三角形ABC的边长为6，在AC，BC边上各取一点E，F，连接AF，BE相交于点P．

(1)若AE=CF；
①求证：AF=BE，并求∠APB的度数；
②若AE=2，试求AP⋅AF的值；
(2)若AF=BE，当点E从点A运动到点C时，试求点P经过的路径长．
25. (本小题8.0分)
已知△ABC和△EFC中，∠ABC=∠EFC=α，点E在△ABC内，且∠CAE+∠CBE=90°．


(1)如图①，当△ABC和△EFC都是等腰三角形，且α=90°时，连结BF．
①求证：△ACE∽△BCF；
②若BE=1，AE=2，求EF的长．
(2)如图②，当∠ACB=∠ECF，且α=90°时，若CFCE=k，BE=1，AE=2，CE=3，求k的值．
答案和解析

1.【答案】D 
【解析】
【分析】
本题主要考查了分式方程的解，二次函数图象与系数的关系，解答本题的关键是掌握分式方程的解法，抛物线对称轴的求法；首先根据分式方程有非负整数解得出a是偶数，偶数a满足a⩽4且a≠−2，然后根据抛物线的对称轴在y轴左侧得出a>−6，综合上述情况得出偶数a满足−6 【解答】
解：将关于x的分式方程1x−3+x+a3−x=1去分母，得：1−x+a=x−3，
解得x=4−a2，
∵关于x的分式方程1x−3+x+a3−x=1有非负整数解，
∴4−a是偶数且4−a⩾0且4−a2−3≠0，
∴a是偶数，偶数a满足a⩽4且a≠−2，
∵关于x的二次函数y=4x2+(a+6)x−a−3其对称轴在y轴左侧，
∴x=−a+62×4<0，
解得a>−6，
∴偶数a满足−6 ∴符合条件的整数a的值有−4，0，2，4，
∵−4+0+2+4=2．
∴符合条件的所有整数a的和是2．
故选：D．  
2.【答案】B 
【解析】
【分析】
本题考查二次函数的性质和二次函数图象上点的坐标特征，掌握函数性质并结合分析图象的解题能力是解决本题的关键．
根据函数的性质和函数的图形，依次分析①②③④，选出正确的即可．
【解答】
解：①把(2,1)和(0,0)代入二次函数，等号成立，故对于任何满足条件的a，该二次函数的图象都经过点(2,1)和(0,0)两点符合题意，①正确，
②对称轴x0=−2a−122a=1−14a，由a<0得，x0>1，故若该函数图象的对称轴为直线x=x0，则必有1 ③当x≥0时，根据二次函数的性质，y先随x的增大而增大，到达顶点后，y随着x的增大而减小，故当x≥0时，y随x的增大而增大不符合题意，③错误，
④若P(4,y1)，Q(4+m,y2)(m>0)是函数图象上的两点，如果y1>y2总成立，说明抛物线对称轴x0=1−14a≤4，解得：a≤−112，④正确，
即正确的为①④，
故选B．  
3.【答案】B 
【解析】解：因为一副扑克牌中共有54张牌，去掉大小王的扑克牌，还剩52张，红桃为13张．
则抽到红桃的概率为：1352=14．
故选：B．
根据生活常识可以知道一副扑克牌中共有54张牌，去掉大小王的扑克牌，还剩52张，其中包括方块13张，梅花13张，黑桃13张，红桃13张，进而得出答案．
本题考查随机事件概率的求法：如果一个事件有n种可能，而且这些事件的可能性相同，其中事件A出现m种结果，那么事件A的概率P(A)=mn．

4.【答案】C 
【解析】解：P(中心对称图形)=35．
故选：C．
任意翻开一张卡片，共有5种情况，其中是中心对称图形的有平行四边形，矩形，正六边形3种，所以概率是35．
本题关键理解什么是中心对称图形，然后根据事件的总数和出现中心对称图形的次数求出概率．

5.【答案】B 
【解析】
【分析】
本题主要考查方差、全面调查与抽样调查、随机事件以及概率的意义等知识.解答本题的关键是熟练掌握方差性质、概率的意义以及抽样调查与普查的特点，此题难度不大.利用事件的分类、普查和抽样调查的特点、概率的意义以及方差的性质即可作出判断．
【解答】
解：A.掷一枚均匀的骰子，骰子停止转动后，6点朝上是随机事件，此选项错误；
B.甲、乙两人在相同条件下各射击10次，他们的成绩平均数相同，方差分别是S甲2=0.4，S乙2=0.6，则甲的射击成绩较稳定，此选项正确；
C.“明天降雨的概率为12”，表示明天有可能降雨，此选项错误；
D.了解一批电视机的使用寿命，适合用抽查的方式，此选项错误．
故选B．
  
6.【答案】B 
【解析】解：∵四边形ABCD是正方形
∴∠BAC=∠DAC=45°，
∵在△APE和△AME中，
∠PAE=∠MAEAE=AE∠AEP=∠AEM，
∴△APE≌△AME(ASA)，故①正确；
∴PE=EM=12PM，
同理，FP=FN=12NP，
∵正方形ABCD中，AC⊥BD，
又∵PE⊥AC，PF⊥BD，
∴∠PEO=∠EOF=∠PFO=90°，且△APE中AE=PE，
∴四边形PEOF是矩形，
∴PF=OE，
∴PE+PF=OA，
又∵PE=EM=12PM，FP=FN=12NP，OA=12AC，
∴PM+PN=AC，故②正确；
∵四边形PEOF是矩形，
∴PE=OF，
在直角△OPF中，OF2+PF2=PO2，
∴PE2+PF2=PO2，故③正确;
∵△BNF是等腰直角三角形，而△POF不一定是，故④错误；
∵OA垂直平分线段PM，OB垂直平分线段PN，
∴OM=OP，ON=OP，
∴OM=OP=ON，
∴点O是△PMN的外接圆的圆心，
∵∠MPN=90°，
∴MN是直径，
∴M，O，N共线，故⑤正确．
故选B．
依据正方形的性质以及等腰直角三角形、矩形的判定方法即可判断△APM和△BPN以及△APE、△BPF都是等腰直角三角形，四边形PEOF是矩形，从而作出判断．
本题考查正方形的性质、矩形的判定、等腰直角三角形，全等三角形的判定与性质，以及三角形的外接圆与外心．

7.【答案】B 
【解析】
【分析】
本题考查动点最值问题、等边三角形的性质、点与圆的位置关系、勾股定理等知识，解题的关键是正确寻找点M的运动路径，学会利用特殊位置解决轨迹问题中的直径的长，属于中考选择题中的压轴题．
因为△PBM是等边三角形，点P在圆心为A半径为2的⊙A上运动，推出点M的运动路径也是圆，当点P1(4,0)时，点M与E重合，当P2(0,0)时，点M与F重合，易证点M所在的⊙O′的直径EF=OP1=4，可得O′(72,332)，进而求出AO′的长，再利用点与圆的位置关系即可解决问题．
【解答】
解：如图，

∵△PBM是等边三角形，点P在圆心为A半径为2的⊙A上运动，
∴点M的运动路径也是圆，
当点P1(4,0)时，点M与E重合，△BEP1是等边三角形；当P2(0,0)时，点M与F重合，△BFP2是等边三角形；
∴点M所在的⊙O′的直径EF=OP1=4，∠OBF=60°，
∴BE=BP1=OB−OP1=1
∴O′B=3，
作O′H⊥AB于点H，
则∠BO′H=30°，
∴BH=12O′B=32，
由勾股定理得：O′H=O′B2−BH2=332，
∵OH=OB−BH=5−32=72，
∴O′(72,332)，
∵A(2,0)，
∴AO′=72−22+3322=3，
当点M在AO′的延长线上时，AM的值最大，最大值为3+2=5，
故选：B．  
8.【答案】A 
【解析】解：如图，延长AE交DC的延长线于点H，

∵点E是CM的中点，
∴ME=EC，
∵AB//CD，
∴∠MAE=∠H，∠AME=∠HCE，
∴△AME≌△HCE(AAS)，
∴AE=EH，
又∵∠ADH=90°，
∴DE=AE=EH，
∵AE绕点E顺时针旋转90°得到EF，
∴AE=EF，∠AEF=90°，
∴AE=DE=EF，故①正确；
∵AE=DE=EF，
∴∠DAE=∠ADE，∠EDF=∠EFD，
∵∠AEF+∠DAE+∠ADE+∠EDF+∠EFD=360°，
∴2∠ADE+2∠EDF=270°，
∴∠ADF=135°，
∴∠CDF=∠ADF−∠ADC=135°−90°=45°，故②正确；
如图，连接FC，过点C作CF′⊥DF于F′，

∵∠CDF=45°，
∴点F在DF上运动，
∴当CF⊥DF时，CF有最小值为CF′的长度，
∵CD=2，∠CDF=45°，
∴CF′=22=2，即CF有最小值为2，故③正确，
故选：A．
延长AE交DC的延长线于点H，由“AAS”可证△AME≌△HCE，可得AE=EH，由直角三角形的性质可得AE=EF=EH，可判断①；由四边形内角和定理可求2∠ADE+2∠EDF=270°，可得∠ADF=135°，可判断②；连接FC，过点C作CF′⊥DF于F′，由∠CDF=45°，知点F在DF上运动，即得当CF⊥DF时，CF有最小值为CF′的长度，而CF′=2，即CF有最小值为2，可判断③正确．
本题考查了正方形的性质，全等三角形的判定和性质，旋转的性质等知识，解题的关键是掌握折叠的性质，正确作辅助线，构造全等三角形．

9.【答案】B 
【解析】
【分析】
本题考查轨迹，相似三角形的判定和性质，解直角三角形等知识，解题的关键是正确寻找点Q的运动轨迹，属于中考选择题中的压轴题．
如图，由题意，点P在△ABC的三条边上运动一周时，点Q运动的轨迹是△MGH.利用相似三角形的性质求出MG，GH，MH，利用勾股定理的逆定理，证明△MHG是直角三角形，即可解决问题．
【解答】
解：如图，由题意，点P在△ABC的三条边上运动一周时，点Q运动的轨迹是△MGH．

∵A(−1,1)，B(−1,4)，C(−5,4)，
∴AB=3，BC=4，AC=5，
∵OMOA=OGOB=22，∠AOB=∠MOG，
∴△AOB∽△MOG，
∴MGAB=OMOA=22，
∴MG=322，
同法可得，GH=22BC=22，MH=22AC=522，
∴MH2=HG2+GM2=252
∴点Q的轨迹形成的封闭图形面积=12×322×22=3．
故选：B．
  
10.【答案】A 
【解析】解：过D作DE⊥BC于E，
则∠DEC=∠DEB=90°，
∵AD//BC，∠ABC=90°，
∴∠DAB=∠ABC=90°，
∴四边形ABED是矩形，
∴BE=AD=2，DE=AB=27，
∵将△ABC绕点C顺时针方向旋转后得△A′B′C，
∴∠DB′C=∠ABC=90°，B′C=BC，A′C=AC，∠A′CA=∠B′CB，
∴△A′CA∽△B′CB，
∴A′AB′B=ACBC，
∵△B′CD为等腰三角形，
∴△B′CD为等腰直角三角形，
∴CD=2B′C，
设B′C=BC=x，则CD=2x，CE=x−2，
∵CD2=CE2+DE2，
∴(2x)2=(x−2)2+(27)2，
∴x=4(负值舍去)，
∴BC=4，
∴AC=AB2+BC2=211，
∴A′A2=2114，
∴A′A=11，
故选：A．
过D作DE⊥BC于E，则∠DEC=∠DEB=90°，根据矩形的性质得BE=AD=2，DE=AB=27，根据旋转的性质得到∠DB′C=∠ABC=90°，B′C=BC，A′C=AC，∠A′CA=∠B′CB，推出△B′CD为等腰直角三角形，得到CD=2B′C，设B′C=BC=x，则CD=2x，CE=x−2，根据勾股定理即可得到结论．
本题考查了旋转的性质，等腰直角三角形的性质，矩形的判定和性质，相似三角形的判定和性质，勾股定理，正确的识别图形是解题的关键．

11.【答案】B 
【解析】
【分析】
本题考查了矩形的性质，相似三角形的判定与性质，勾股定理等知识．
设AD=3x，AB=2x，证明△CEP∽△BFP，利用勾股定理及相似三角形的性质得BE=BF=2x，结合平行线的性质及等腰三角形的性质可判断①正确；证明△EBP∽△EFB，得出比例式，等量代换可判断②正确；证明△FBP∽△FGE，得出比例式结合直角三角形的性质可判断③错误；证明△AOB和△POB是直角三角形，利用勾股定理表示出相关线段的长度，计算可判断④正确，进而得出结论．
【解答】
解：设AD=3x，AB=2x，
∵四边形ABCD是矩形，
∴AD=BC，CD=AB，∠D=∠C=∠ABC=90∘，DC//AB，
∴BC=3x，CD=2x，
∵E为DC的中点，
∴CE=12CD=x，
∴BE=2x，
∵CE//BF，
∴△CEP∽△BFP，∠CEP=∠BFP，
∴CPBP=CEBF=EPPF=12，
∴BF=2CE=2x，
∴BE=BF，
∴∠BFP=∠BEF，
∴∠BEF=∠CEP，
∴EP平分∠CEB，故①正确；
在Rt△BCE中，CE=12BE，
∴∠CBE=30°，∠BEC=60°，
∴∠BEP=∠BFP=30°，
∴△EBP∽△EFB，
∴BEEF=BPBF，
∴BE⋅BF=BP·EF，
∴BF2=PB⋅EF，故②正确；
过点E作EG⊥AF于G，

∴∠EGF=90∘，
∴△FBP∽△FGE，
∴PFEF=BPEG=23，
∴PF=23EF，
在Rt△EGF中，∠BFP=30°，
∴EF=2EG=2AD，
∴PF=43AD，
∴PF⋅EF=83AD2≠2AD2，故③错误；
∵AB=BF，∠ABP=∠FBP，BP=BP，
∴△ABP≌△FBP，
∴∠PAB=∠BFP=30°，
∵∠ABO=∠CEB=60°，
∴∠AOB=90°，
在Rt△AOB和Rt△POB中，由勾股定理得，
AO=3x，PO=33x，
∴EF⋅EP=23x⋅233x=4x2，
4AO⋅PO=4×3x⋅33x=4x2．
∴EF⋅EP=4AO⋅PO，故④正确．
故选B．  
12.【答案】A 
【解析】
【分析】
此题考查的是等腰直角三角形的性质和相似三角形的判定和性质，利用等腰直角三角形性质利用两边对应成比例，夹角相等证明BAE∽△CAD，判定①；证明△PME∽△AMD，根据相似三角形性质可判断②；证明△PMA∽△EMD和△CAP∽△CMA，由相似三角形性质判定③．
【解答】
解：∵△ABC和△AED均为等腰直角三角形，
∴AC=2AB，AD=2AE，∠BAC=∠BCA=∠EAD=∠EDA=45∘，
∴ACAB=ADAE=2，
∵∠BAC=∠EAD，
∴∠BAE=∠CAD，
∴△BAE∽△CAD，
∴ ①正确．
∵△BAE∽△CAD，
∴∠BEA=∠CDA，
∵∠PME=∠AMD，
∴△PME∽△AMD，
∴MPMA=MEMD，
∴MP⋅MD=MA⋅ME，
∴ ②正确．
∵MP⋅MD=MA⋅ME，
∴MPME=MAMD，
又∠PMA=∠DME，
∴△PMA∽△EMD，
∴∠APD=∠AED=90∘，
∵∠CAM=180∘−∠BAC−∠EAD=90∘=∠APC，
∵∠ACP=∠MCA，
∴△CAP∽△CMA，
∴ACCM=CPAC，
∴AC2=CP⋅CM，
∵AC=2BC，
∴2CB2=CP⋅CM，
∴ ③正确，
故选A．
  
13.【答案】y=x+42+6 
【解析】
【分析】
本题考查了二次函数与几何变换：由于抛物线平移后的形状不变，故a不变，所以求平移后的抛物线解析式通常可利用两种方法：一是求出原抛物线上任意两点平移后的坐标，利用待定系数法求出解析式；二是只考虑平移后的顶点坐标，即可求出解析式．
先得到抛物线y=x2的顶点坐标(0,0)，再根据点平移的规律得到点(0,0)平移后的对应点的坐标为(−4,6)，然后根据顶点式写出平移后的抛物线解析式．
【解答】
解：抛物线y=x2的顶点坐标为(0,0)，把点(0,0)先向左平移4个单位，再向下平移3个单位得到对应点的坐标为(−4,6)，所以平移后的抛物线解析式为y=x+42+6．
故答案为y=x+42+6．  
14.【答案】34 
【解析】
【分析】本题考查了概率的计算和三角形的三边关系.能得出搭成一个三角形的情况的几种情况是关键.先列举出所有的情况和根据三角形的三边关系求出搭成一个三角形的情况，再由概率公式即可求得．
【解答】解：根据题意，从4根细木棒中任取3根，有2、3、4;3、4、5;2、3、5;2、4、5，共4种取法，而能搭成一个三角形的有2、3、4;3、4、5;2、4、5，共3种，故恰好能搭成一个三角形的概率为34．
故答案为34．  
15.【答案】23 
【解析】解：过点O作OD⊥AB交AB于点D，连接OA，
∵OA=2OD=2cm，
∴AD=OA2−OD2=22−12=3cm，
∵OD⊥AB，
∴AB=2AD=23cm．
故答案为：23．
通过作辅助线，过点O作OD⊥AB交AB于点D，根据折叠的性质可知OA=2OD，根据勾股定理可将AD的长求出，通过垂径定理可求出AB的长．
本题综合考查垂径定理和勾股定理的运用．

16.【答案】152 ；202 
【解析】解：∵AE⊥l，BF⊥l，
∵∠ANE=45°，
∴△ANE和△BNF是等腰直角三角形，
∴AE=EN，BF=FN，
∵EF=15米，FM=2米，MN=8米，
∴AE=EN=15+2+8=25(米)，BF=FN=2+8=10(米)，
∴AN=252，BN=102，
∴AB=AN−BN=152(米)；
过C作CH⊥l于H，过B作PQ//l交AE于P，交CH于Q，
∴AE//CH，
∴四边形PEHQ和四边形PEFB是矩形，
∴PE=BF=QH=10，PB=EF=15，BQ=FH，
∵∠1=∠2，∠AEF=∠CHM=90°，
∴△AEF∽△CHM，
∴CHHM=AEEF=2515=53，
∴设MH=3x，CH=5x，
∴CQ=5x−10，BQ=FH=3x+2，
∵∠APB=∠ABC=∠CQB=90°，
∴∠ABP+∠PAB=∠ABP+∠CBQ=90°，
∴∠PAB=∠CBQ，
∴△APB∽△BQC，
∴APBQ=PBCQ，
∴153x+2=155x−10，
∴x=6，
∴BQ=CQ=20，
∴BC=202，
故答案为152；202．
根据已知条件得到△ANE和△BNF是等腰直角三角形，求得AE=EN=15+2+8=25(米)，BF=FN=2+8=10(米)，于是得到AB=AN−BN=152(米)；过C作CH⊥l于H，过B作PQ//l交AE于P，交CH于Q，根据矩形的性质得到PE=BF=QH=10，PB=EF=15，BQ=FH，根据相似三角形的性质即可得到结论．
本题考查了相似三角形的应用，矩形的性质，等腰直角三角形的判定和性质，正确的识别图形是解题的关键．

17.【答案】解：(1)∵二次函数的对称轴是直线x=1，
∴−b2×1=1，
∴b=−2，
将A(−1,0)代入y=x2−2x+c中，
解得c=−3．
∴二次函数的表达式为y=x2−2x−3；
(2)∵二次函数y=x2+bx+c的图象与x轴交于A，B两点，
A(−1,0)，对称轴为直线x=1，
∴B(3,0)，
∴当−1 ∴当y<0时，x的取值范围为−1 (3)①若a+1≤1，即a≤0时，
则当x=a+1时，函数值最小，
∴(a+1)2−2(a+1)−3=2a，
解得：a=1−5或a=1+5(舍去)；
②如a<1 则当x=1时函数值最小，
∴1−2−3=2a，
解得：a=−2(不合题意)；
③若a≥1，
则当x=a时函数值最小，
∴a2−2a−3=2a，
解得：a=2+7或a=2−7(舍去)，
∴a的值为1−5或2+7． 
【解析】(1)二次函数的对称轴是直线x=1，求出b=−2，将A(−1,0)代入y=x2−2x+c中，即可求解；
(2)根据点A，B关于对称轴x=1对称，求出点B坐标，再结合图象求出x的取值范围；
(3)分a+1≤1，a<1 本题考查的是抛物线与x轴的交点，关键是对给定的自变量的取值范围与对称轴位置关系的讨论．

18.【答案】解：(1)由题意，得a+b+1=04a+2b+1=1
解得a=1b=−2
所以，该函数表达式为y=x2−2x+1．
并且该函数图象的顶点坐标为(1,0)．
(2)由题意，得P=p2+p+1，Q=q2+q+1，
所以 P+Q=p2+p+1+q2+q+1
=p2+q2+4
=(2−q)2+q2+4
=2(q−1)2+6≥6，
由条件p≠q，知q≠1.所以 P+Q>6，得证． 
【解析】(1)考查使用待定系数法求二次函数解析式，属于基础题，将两点坐标代入，解二元一次方程组即可；
(2)已知a=b=1，则y=x2+x+1.容易得到P+Q=p2+p+1+q2+q+1，利用p+q=2，即p=2−q代入对代数式P+Q进行化简，并配方得出P+Q=2(q−1)2+6≥6.最后注意利用p≠q条件判断q≠1，得证．
本题主要考查了待定系数法求解二次函数表达式，以及二次函数图象的顶点坐标，代数式的化简，并利用配方法判断代数式的取值范围．
第(2)小问的关键是利用p+q=2，首先对代数式P+Q化简，然后配方说明P+Q的范围，另外注意q≠1．

19.【答案】解：(1)将标有数字1和3的扇形两等分可知转动转盘一次共有6种等可能结果，其中转出的数字是−2的有2种结果，
所以转出的数字是−2的概率为26=13；

(2)列表如下：

−2
−2
1
1
3
3
−2
4
4
−2
−2
−6
−6
−2
4
4
−2
−2
−6
−6
1
−2
−2
1
1
3
3
1
−2
−2
1
1
3
3
3
−6
−6
3
3
9
9
3
−6
−6
3
3
9
9
由表可知共有36种等可能结果，其中数字之积为正数的有20种结果，
所以这两次分别转出的数字之积为正数的概率为2036=59． 
【解析】(1)将标有数字1和3的扇形两等分可知转动转盘一次共有6种等可能结果，其中转出的数字是−2的有2种结果，根据概率公式计算可得；
(2)列表得出所有等可能结果，从中找到乘积为正数的结果数，再利用概率公式求解可得．
本题考查的是用列表法或画树状图法求概率．注意列表法或画树状图法可以不重复不遗漏的列出所有可能的结果，列表法适合于两步完成的事件，树状图法适合两步或两步以上完成的事件．用到的知识点为：概率=所求情况数与总情况数之比．

20.【答案】解：(1)小玲摸到C棋的概率等于310；
(2)小玲在这一轮中胜小军的概率是49．
(3)①若小玲摸到A棋，小玲胜小军的概率是59；
②若小玲摸到B棋，小玲胜小军的概率是79；
③若小玲摸到C棋，小玲胜小军的概率是49；④若小玲摸到D棋，小玲胜小军的概率是19．
由此可见，小玲希望摸到B棋，小玲胜小军的概率最大． 
【解析】本题考查概率问题中的公平性问题，解决本题的关键是计算出各种情况的概率，然后比较即可．概率相等则公平，否则不公平．
【命题意图】情景简单，背景公平．通过摸棋游戏这个活动考查学生对概率知识的理解，第(3)小题则是需要学生对多种情形进行分析、比较方可得出答案，要求学生有严谨的思维．用到的知识点为：概率=所求情况数与总情况数之比．

21.【答案】解：(1)四边形BE′FE是正方形，
理由如下：
∵将Rt△ABE绕点B按顺时针方向旋转90°，
∴∠AEB=∠CE′B=90°，BE=BE′，∠EBE′=90°，
又∵∠BEF=90°，
∴四边形BE′FE是矩形，
又∵BE=BE′，
∴四边形BE′FE是正方形；
(2)CF=E′F；
理由如下：如图②，过点D作DH⊥AE于H，

∵DA=DE，DH⊥AE，
∴AH=12AE，
∴∠ADH+∠DAH=90°，
∵四边形ABCD是正方形，
∴AD=AB，∠DAB=90°，
∴∠DAH+∠EAB=90°，
∴∠ADH=∠EAB，
又∵AD=AB，∠AHD=∠AEB=90°，
∴△ADH≌△BAE(AAS)，
∴AH=BE=12AE，
∵将Rt△ABE绕点B按顺时针方向旋转90°，
∴AE=CE′，
∵四边形BE′FE是正方形，
∴BE=E′F，
∴E′F=12CE′，
∴CF=E′F；
(3)如图①，过点D作DH⊥AE于H，

∵四边形BE′FE是正方形，
∴BE′=E′F=BE，
∵AB=BC=15，CF=3，BC2=E′B2+E′C2，
∴225=E′B2+(E′B+3)2，
∴E′B=9=BE，
∴CE′=CF+E′F=12，
由(2)可知：BE=AH=9，DH=AE=CE′=12，
∴HE=AE−AH=12−9=3，
∴DE=DH2+HE2=144+9=317． 
【解析】
【分析】
本题是四边形综合题，考查了正方形的判定和性质，旋转的性质，全等三角形的判定和性质，等腰三角形的性质等知识，灵活运用这些性质进行推理是本题的关键．
(1)由旋转的性质可得∠AEB=∠CE′B=90°，BE=BE′，∠EBE′=90°，由正方形的判定可证四边形BE′FE是正方形；
(2)过点D作DH⊥AE于H，由等腰三角形的性质可得AH=12AE，DH⊥AE，由“AAS”可得△ADH≌△BAE，可得AH=BE=12AE，由旋转的性质可得AE=CE′，可得结论；
(3)过点D作DH⊥AE于H，利用勾股定理可求BE=BE′=9，再利用勾股定理可求DE的长．  
22.【答案】解：(1)证明：在Rt△EBC中，M是斜边EC的中点，
∴BM=12EC=EM=MC，
∴∠EMB=2∠ECB．
在Rt△EDC中，M是斜边EC的中点，
∴DM=12EC=EM=MC．
∴∠EMD=2∠ECD．
∴BM=DM，∠EMD+∠EMB=2(∠ECD+∠ECB)，
∵∠ECD+∠ECB=∠ACB=45°，
∴∠BMD=2∠ACB=90°，即BM⊥DM．
(2).(1)中的结论仍成立，
延长DM至点F，使得DM=MF，
连接CD和EF，连接BD，连接BF、FC，延长ED交AC于点H．

∵DM=MF，EM=MC，
∴四边形CDEF是平行四边形，
∴DE//CF，ED=CF，
∵ED=AD，
∴AD=CF．
∵DE//CF，
∴∠AHE=∠ACF．
∵∠BAD=45°−∠DAH=45°−(90°−∠AHE)
=∠AHE−45°，
∠BCF=∠ACF−45°，
∴∠BAD=∠BCF．
又∵AB=BC，
∴△ABD≌△CBF，
∴BD=BF，∠ABD=∠CBF，
∵∠ABD+∠DBC=∠CBF+∠DBC，
∴∠DBF=∠ABC=90°．
在Rt△DBF中，由BD=BF，DM=MF，得BM=DM且BM⊥DM． 
【解析】本题考查了等腰直角三角形的性质，全等三角形的性质和判定，直角三角形斜边上的中线，解题的关键是学会添加辅助线构造全等三角形，属于中考常考题型．
(1)利用直角三角形斜边上的中线等于斜边的一半得出BM=12EC=EM=MC，DM=12EC=EM=MC，再根据外角性质得到∠EMB=2∠ECB，∠EMD=2∠ECD，即可得解；
(2)延长DM至点F，使得DM=MF ，延长ED交AC于点H，通过证明△ABD≌△CBF，得出BD=BF ，∠ABD=∠CBF，继而可得答案．

23.【答案】解：AC与BD是相等，理由如下；
过点O作OE⊥AB于点E，
∵OA=OB，
∴AE=BE，
在⊙O中，
∵OE⊥CD，
∴CE=DE，
∴AC=BD． 
【解析】本题考查的是垂径定理，根据题意作出辅助线，利用垂径定理求解是解答此题的关键．
过点O作OE⊥AB，由等腰三角形的性质可知AE=BE，再由垂径定理可知CE=DE，故可得出结论．

24.【答案】解：(1)①证明：∵△ABC为等边三角形，
∴AB=AC，∠C=∠CAB=60°，
又∵AE=CF，
在△ABE和△CAF中，
AB=AC∠BAE=∠ACFAE=CF，
∴△ABE≌△CAF(SAS)，
∴AF=BE，∠ABE=∠CAF．
又∵∠APE=∠BPF=∠ABP+∠BAP，
∴∠APE=∠BAP+∠CAF=60°．
∴∠APB=180°−∠APE=120°．
②∵∠C=∠APE=60°，∠PAE=∠CAF，∴△APE∽△ACF，
∴APAC=AEAF，即AP6=2AF，所以AP⋅AF=12

(2)若AF=BE，有AE=BF或AE=CF两种情况．
①当AE=CF时，点P的路径是一段弧，由题目不难看出当E为AC的中点的时候，点P经过弧AB的中点，此时△ABP为等腰三角形，且∠ABP=∠BAP=30°，
∴∠AOB=120°，
又∵AB=6，
∴OA=23，
点P的路径是l=nπr180=120π⋅23180=433π．
②当AE=BF时，点P的路径就是过点C向AB作的垂线段的长度；因为等边三角形ABC的边长为6，所以点P的路径为：62−32=33．
所以，点P经过的路径长为433π或33． 
【解析】本题考查了等边三角形性质的综合应用以及相似三角形的判定及性质的应用，解答本题的关键是注意转化思想的运用．
(1)①证明△ABE≌△CAF，借用外角即可以得到答案；②利用勾股定理求得AF的长度，再用平行线分线段成比例定理或者三角形相似定理求得APAF的比值，即可以得到答案．
(2)当点F靠近点C的时候点P的路径是一段弧，由题目不难看出当E为AC的中点的时候，点P经过弧AB的中点，此时△ABP为等腰三角形，继而求得半径和对应的圆心角的度数，求得答案．点F靠近点B时，点P的路径就是过点B向AC作的垂线段的长度；

25.【答案】解：(1)①∵△ABC和△EFC都是等腰三角形，且∠ABC=∠EFC=α=90°，
∴ACBC=ECFC=2，∠ACB=∠ECF=45°，
∴∠ACE=∠BCF，
∴△ACE∽△BCF；
②∵△ACE∽△BCF，
∴AEBF=ACBC=2，∠CAE=∠CBF，
∴BF=AE2=22=2，
∵∠CAE+∠CBE=90°．
∴∠CBF+∠CBE=90°.即∠EBF=90°，
∴EF=BF2+BE2=3； 
(2)连接BF，如图2，
∵∠ACB=∠ECF，∠ABC=∠EFC=α=90°，
∴△ABC∽△EFC，
∴CBCF=CACE，
∴CACB=CECF，
∵∠ACB=∠ECF，
∴∠ACE=∠BCF，
∴△ACE∽△BCF，
∴BFAE=CFCE=k，∠CBF=∠CAE，
∴BF=k⋅AE=2k，
∵∠CAE+∠CBE=90°．
∴∠CBF+∠CBE=90°．
∴∠EBF=90°，
∴BF2+BE2=EF2=CE2−CF2，
∵CFCE=k，CE=3，
∴CF=3k，
∴(2k)2+12=32−(3k)2，
∴k=22613.    
 
【解析】此题是相似形综合题，主要考查了等腰直角三角形的性质，勾股定理，相似三角形的判定和性质，判断出∠EBF=90°是解本题的关键．
(1)①先判断出∠BCF=∠ACE，再判断出CEAC=CFBC，即可得出结论；
②先判断出∠CBF=∠CAE，进而判断出∠EBF=90°，再求出BF，最后用勾股定理求解即可得出结论；
(2)先判断出△ABC∽△EFC，进而判断出△BCF∽△ACE，进而表示出BF=2k，再表示出CF=3k，最后用勾股定理得求解即可得出结论．