初中数学浙教版八年级上册第5章 一次函数综合与测试单元测试同步训练题
展开浙教版初中数学八年级上册第五单元《一次函数》单元测试卷
考试范围:第五章;考试时间:120分钟;总分:120分
学校:___________姓名:___________班级:___________考号:___________
第I卷(选择题)
一、选择题(本大题共12小题,共36.0分。在每小题列出的选项中,选出符合题目的一项)
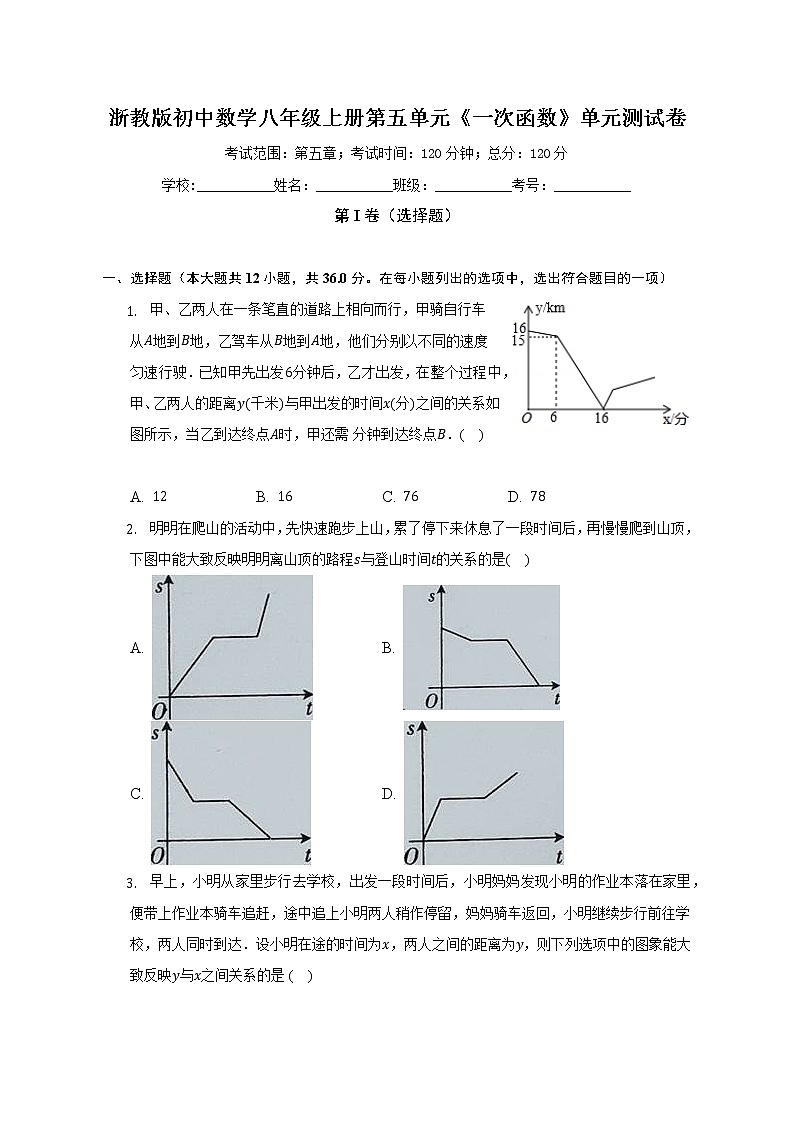
1. 甲、乙两人在一条笔直的道路上相向而行,甲骑自行车从A地到B地,乙驾车从B地到A地,他们分别以不同的速度匀速行驶.已知甲先出发6分钟后,乙才出发,在整个过程中,甲、乙两人的距离y(千米)与甲出发的时间x(分)之间的关系如图所示,当乙到达终点A时,甲还需分钟到达终点B.( )
A. 12 B. 16 C. 76 D. 78
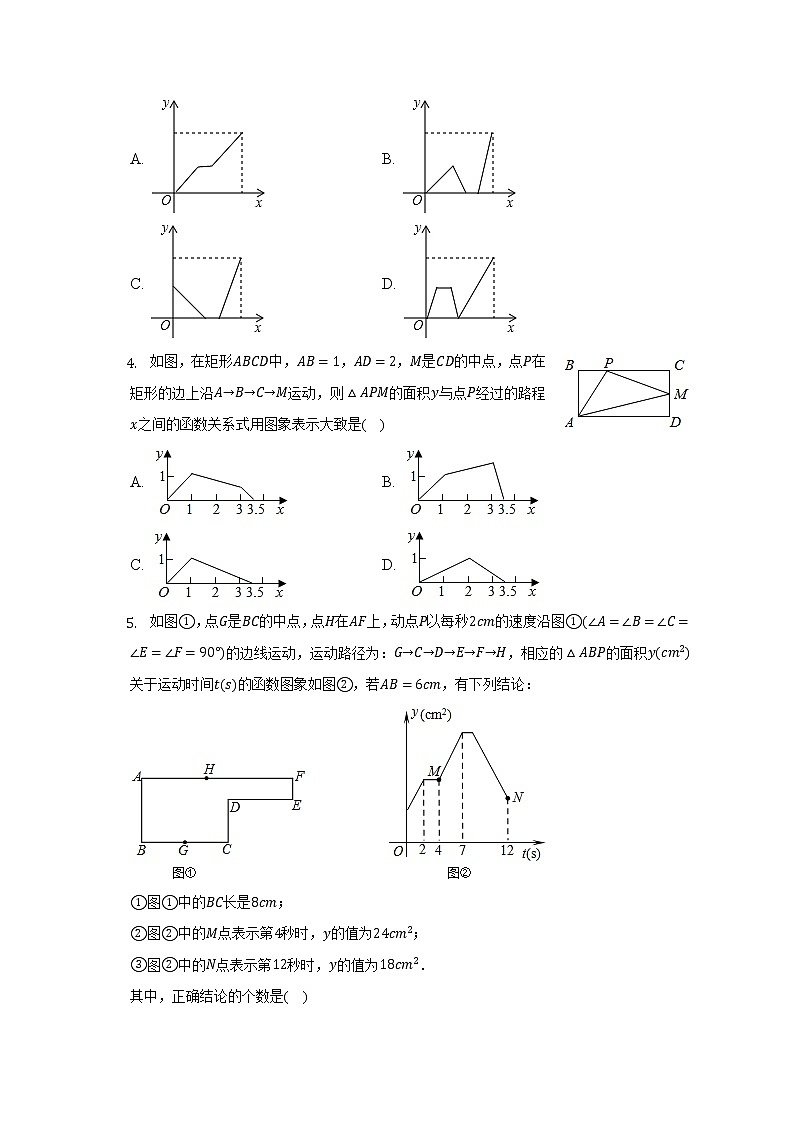
2. 明明在爬山的活动中,先快速跑步上山,累了停下来休息了一段时间后,再慢慢爬到山顶,下图中能大致反映明明离山顶的路程s与登山时间t的关系的是( )
A. B.
C. D.
3. 早上,小明从家里步行去学校,出发一段时间后,小明妈妈发现小明的作业本落在家里,便带上作业本骑车追赶,途中追上小明两人稍作停留,妈妈骑车返回,小明继续步行前往学校,两人同时到达.设小明在途的时间为x,两人之间的距离为y,则下列选项中的图象能大致反映y与x之间关系的是( )
A. B.
C. D.
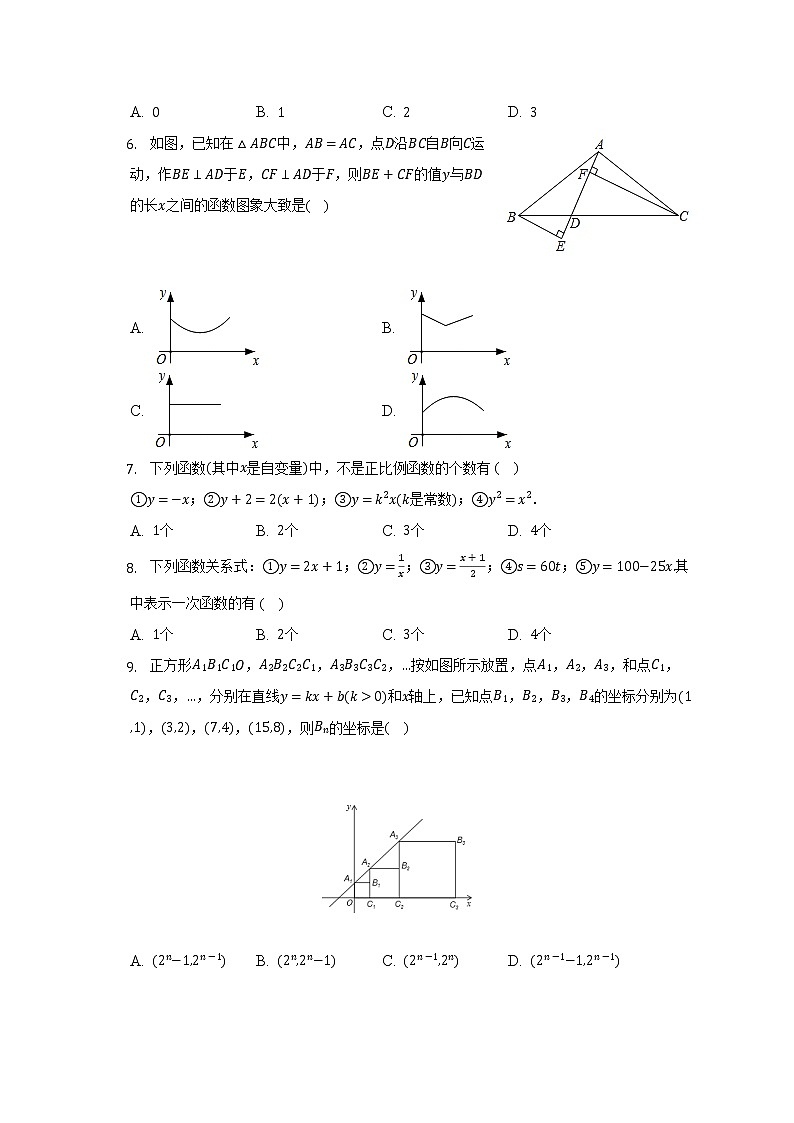
4. 如图,在矩形ABCD中,AB=1,AD=2,M是CD的中点,点P在矩形的边上沿A→B→C→M运动,则△APM的面积y与点P经过的路程x之间的函数关系式用图象表示大致是( )
A. B.
C. D.
5. 如图①,点G是BC的中点,点H在AF上,动点P以每秒2cm的速度沿图①(∠A=∠B=∠C=∠E=∠F=90°)的边线运动,运动路径为:G→C→D→E→F→H,相应的△ABP的面积y(cm2)关于运动时间t(s)的函数图象如图②,若AB=6cm,有下列结论:
①图①中的BC长是8cm;
②图②中的M点表示第4秒时,y的值为24cm2;
③图②中的N点表示第12秒时,y的值为18cm2.
其中,正确结论的个数是( )
A. 0 B. 1 C. 2 D. 3
6. 如图,已知在△ABC中,AB=AC,点D沿BC自B向C运动,作BE⊥AD于E,CF⊥AD于F,则BE+CF的值y与BD的长x之间的函数图象大致是( )
A. B.
C. D.
7. 下列函数(其中x是自变量)中,不是正比例函数的个数有( )
①y=−x;②y+2=2(x+1);③y=k2x(k是常数);④y2=x2.
A. 1个 B. 2个 C. 3个 D. 4个
8. 下列函数关系式:①y=2x+1;②y=1x;③y=x+12;④s=60t;⑤y=100−25x.其中表示一次函数的有( )
A. 1个 B. 2个 C. 3个 D. 4个
9. 正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图所示放置,点A1,A2,A3,和点C1,C2,C3,…,分别在直线y=kx+b(k>0)和x轴上,已知点B1,B2,B3,B4的坐标分别为(1,1),(3,2),(7,4),(15,8),则Bn的坐标是( )
A. (2n−1,2n−1) B. (2n,2n−1) C. (2n−1,2n) D. (2n−1−1,2n−1)
10. 如图,在平面直角坐标系中,A(−1,0),B(2,0),C(a,a+6),D为线段BC的中点,线段AD交线段OC于点E,当线段OE最短时,此时点E的坐标为( )
A. (−34,34) B. (−1,1) C. (−14,1) D. (− 34,34)
11. 小带和小路两个人开车从A城出发匀速行驶至B城.在整个行驶过程中,小带和小路两人的车离开A城的距离y(千米)与行驶的时间t(小时)之间的函数关系如图所示.有下列结论:
①A、B两城相距300千米;
②小路的车比小带的车晚出发1小时,却早到1小时;
③小路的车出发后2.5小时追上小带的车;
④当小带和小路的车相距50千米时,t=54或t=154.
其中正确的结论有( )
A. ①②③④ B. ①②④ C. ①② D. ②③④
12. 甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.则下列结论:
①A,B两城相距300千米;
②乙车比甲车晚出发1小时,却早到1小时;
③乙车出发后2.5小时追上甲车;
④当甲、乙两车相距50千米时,t=54或154.
其中正确的结论有( )
A. 1个 B. 2个 C. 3个 D. 4个
第II卷(非选择题)
二、填空题(本大题共4小题,共12.0分)
13. 甲、乙两人在同一平直的道路上同时、同起点、同方向出发,他们分别以不同的速度匀速跑步1800米(甲的速度大于乙的速度),当甲第一次超出乙300米时,甲停下来等候乙.甲、乙两人会合后,两人分别以原来的速度继续跑向终点,先到终点的人在终点休息.在整个跑步过程中,甲、乙两人之间的距离y(米)与乙出发的时间x(秒)之间的关系如图所示,则当甲到达终点时,乙跑了________米.
14. 某工程队承建一条长为30km的乡村公路,预计工期为120天,若每天修建公路的长度保持不变,则还未完成的公路长度y(km)与施工时间x(天)之间的关系式为y=______.
15. 已知y=2xm−2+3是一次函数,则m =_________.
16. 张师傅驾车从甲地到乙地匀速行驶,已知行驶中油箱剩余油量y(升)与行驶时间t(小时)之间的关系用如图的线段AB表示,根据这个图象求出y与t之间的函数关系式为y=−7.5t+25,那么函数y=−7.5t+25中,t的系数−7.5表示的实际意义是________.
三、解答题(本大题共9小题,共72.0分。解答应写出文字说明,证明过程或演算步骤)
17. (本小题8.0分)
一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发.设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的关系.根据图象解答下列问题:
(1)甲、乙两地之间的距离为 km;
(2)请解释图中点B的实际意义;
(3)求慢车和快车的速度.
18. (本小题8.0分)
快车与慢车分別从甲乙两地同时相向出发,匀速而行,快车到达乙地后停留1h,然后按原路原速返回,快车比慢车晚1h到达甲地,快慢两车距各自出发地的路程y(km)与所用的时x(h)的关系如图所示.
(1)甲乙两地之间的路程为__________km;快车的速度为______km/h;慢车的速度为_______km/h;
(2)出发________h,快慢两车距各自出发地的路程相等;
(3)快慢两车出发___________h相距150km.
19. (本小题8.0分)
如图,在四边形OABC中,OA//BC,∠OAB=90°,O为原点,点C的坐标为(2,8),点A的坐标为(26,0),点D从点B出发,以每秒1个单位长度的速度沿BC向点C运动,点E同时从点O出发,以每秒3个单位长度的速度沿折线OAB运动,当点E达到点B时,点D也停止运动,从运动开始,设D(E)点运动的时间为t秒.
(1)当t为何值时,四边形ABDE是矩形;
(2)当t为何值时,DE=CO?
(3)连接AD,记△ADE的面积为S,求S与t的函数关系式.
20. (本小题8.0分)
某旅游团在某天上午6点从宾馆出发乘车到离宾馆210km的一个景点去游玩.该汽车离开宾馆的距离s(km)与时间t(h)的关系可以用如图所示的折线图表示.根据图像提供的信息解答下列问题:
(1)求该团去这个景点时的平均速度.
(2)该团在这个景点游玩了多长时间?
(3)他们是几点几分返回的宾馆?
21. (本小题8.0分)
新定义:对于关于x的一次函数y=kx+b(k≠0),我们称函数y=kx+bx≤my=−kx−bx>m为一次函数y=kx+b(k≠0)的m变函数(其中m为常数).
例如:对于关于x的一次函数y=x+4的3变函数为y=x+4x≤3y=−x−4x>3.
(1)关于x的一次函数y=−x+1的2变函数为y,则当x=4时,y= .
(2)关于x的一次函数y=x+2的1变函数为y1,关于x的一次函数y=−12x−2的−1变函数为y2,直接写出函数y1和函数y2的交点坐标.
(3)关于x的一次函数y=2x+2的1变函数为y1,关于x的一次函数y=12x−1的m变函数为y2.
①当−3≤x≤3时,函数y1的取值范围是 (直接写出答案).
②若函数y1和函数y2有且仅有两个交点,则m的取值范围是 (直接写出答案).
22. (本小题8.0分)
一次函数y=kx−3的图象与x轴交于点A,与y轴交于点B,△OAB(O为坐标原点)的面积为4,且函数y的值随x的增大而增大.求:
(1)点B的坐标.
(2)点A的坐标及k的值.
23. (本小题8.0分)
如图,在平面直角坐标系中,直线y=14x+1与x轴交于点A,与y轴交于点B,以AB为腰在第二象限作等腰直角△ABC,∠BAC=90°.
(1)求点C的坐标.
(2)E是x轴上的一个动点,是否存在这样的点E,使得|EC−EB|的值最大?如果不存在,请说明理由;如果存在,请求出点E的坐标.
(3)若以Q,A,B为顶点的三角形和△ABC全等(点Q不与点C重合),请直接写出点Q的坐标.
24. (本小题8.0分)
某工厂安排20名技工组装A、B、C三个型号的玩具,按规定每天共组装420件玩具,每名技工只组装同一型号的玩具,且至少有2名技工组装同一个型号的玩具.
玩具型号
A型
B型
C型
每名技工每天组装的数量(个)
22
21
20
每件玩具获得的利润(元)
8
10
6
(1)设工厂安排x名技工组装A型玩具,y名技工组装B型玩具,根据上表提供的信息,求x与y之间的函数关系式,并求出x的取值范围.
(2)工厂如何安排生产任务,可以使得每天在这批玩具上获得的利润最大?请写出相应的生产分配方案并求出每天获得的最大利润值.
25. (本小题8.0分)
某公司有A型产品40件,B型产品60件,分配给下属甲、乙两个商店销售,其中70件给甲店,30件给乙店,且都能卖完.两商店销售这两种产品每件的利润(元)如下表:
A型利润
B型利润
甲店
200
170
乙店
160
150
(1)设分配给甲店A型产品x件,这家公司卖出这100件产品的总利润为W(元),求W关于x的函数关系式,并求出x的取值范围;
(2)若要求总利润不低于17560元,有多少种不同分配方案,并将各种方案设计出来;
(3)为了促销,公司决定仅对甲店A型产品让利销售,每件让利a元,但让利后A型产品的每件利润仍高于甲店B型产品的每件利润.甲店的B型产品以及乙店的A,B型产品的每件利润不变,问该公司又如何设计分配方案,使总利润达到最大?
答案和解析
1.【答案】D
【解析】
【分析】
本题考查了用图象表示变量之间的关系的有关知识,根据路程与时间的关系,可得甲乙的速度,根据相遇前甲行驶的路程除以乙行驶的速度,可得乙到达A站需要的时间,根据相遇前乙行驶的路程除以甲行驶的速度,可得甲到达B站需要的时间,再根据有理数的减法,可得答案.
【解答】
解:由纵坐标看出甲先行驶了1千米,由横坐标看出甲行驶1千米用了6分钟,
甲的速度是1÷6=16千米/分钟,
由纵坐标看出AB两地的距离是16千米,
设乙的速度是x千米/分钟,由题意,得
10x+16×16=16,
解得x=43千米/分钟,
相遇后乙到达A站还需(16×16)÷43=2分钟
相遇后甲到达B站还需10×43÷16=80分钟,
当乙到达终点A时,甲还需80−2=78分钟到达终点B,
故选D.
2.【答案】C
【解析】
【分析】
根据题意可以判断哪个选项中的函数图象符合题意,从而可以解答本题.本题考查函数的图象,解答本题的关键是明确题意,利用数形结合的思想解答.
【解答】
解:由题意可得, 刚开始,小明跑步上山,s随着t的增加而减小,变化趋势比较快,
休息一段时间,这个过程,s随着t的增加不变, 慢慢走完剩下的路程,s随着t的增加而减小,变化趋势比较缓慢,
故选C.
3.【答案】B
【解析】
【分析】
本题考查了函数图象,动点函数的图象的有关知识,读懂题意,把整个过程分解成分段图象是解题的关键.根据题意,把图象分为四段,第一段,小明从家出发去学校到妈妈发现小明的作业本落在家里,第二段妈妈骑车追赶到追上小明,第三段两人稍作停留,第四段妈妈骑车返回,小明继续步行前往学校,两人同时到达.分析图象,然后选择答案.
【解答】
解:根据题意可得,y与x的函数关系的大致图象分为四段,
第一段,小明从家出发去学校到妈妈发现小明的作业本落在家里,两人的距离在慢慢增大,
第二段,妈妈骑车追赶到追上小明,两人的距离在减小,
第三段,两人稍作停留,两人的距离为0,
第四段,妈妈骑车返回,小明继续步行前往学校,两人同时到达,两人的距离在快速增大,
纵观各选项,只有B选项的图象符合.
故选B.
4.【答案】A
【解析】解:①当点P在AB上时,则AP=x,
则y=12AP×BC=12×x×2=x,为一次函数,
当x=1时,y=1;
②当点P在BC上时,
则BP=x−1,PC=1+2−x=3−x,
故y=S矩形ABCD−S△ABP−S△PCM−S△ADM=12×1×2−12[(x−1)×1+(3−x)×12+2×12]=−14x+54,为一次函数,
当x=3时,y=−14×3+54=12;
③当点P在CM上时,y随x的增大而减小,当x=3.5时,y=0,
故选:A.
分点P在AB上、点P在BC上、点P在CM上三种情况,求出函数表达式或确定y随x的变化情况即可求解.
本题考查的是四边形动点问题与一次函数结合,熟悉掌握四边形动点问题的解决办法和一次函数图象的相关性质,运用数形结合的思想是解题的关键.
5.【答案】D
【解析】解:①根据函数图象可以知:从0到2,y随x的增大而增大,经过了2秒,P运动了4cm,因而CG=4cm,BC=8cm,故正确;
②P在CD段时,底边AB不变,高不变,因而面积不变,由图象可知CD=4cm,面积y=12×6×8=24cm2,故正确;
③图2中的N点表示第12秒时,表示点P到达H点,△ABP的面积是18cm2,故正确;
则3个结论正确;
故选:D.
①根据题意得:动点P在GC上运动的时间是2秒,又由动点的速度,可得GC和BC的长;
②由(1)可得BC的长,又由AB=6cm,可以计算出△ABP的面积,计算可得a的值;
③根据图2中的N点表示第12秒时,表示点P到达H点,即可得出△ABP的面积
本题考查了动点问题的函数图象:函数图象是典型的数形结合,图象应用信息广泛,通过看图获取信息,不仅可以解决生活中的实际问题,还可以提高分析问题、解决问题的能力.用图象解决问题时,要理清图象的含义即会识图.
6.【答案】D
【解析】解:过点A作AD′⊥BC于点D′,如图,
由题可知,当点D从点B运动到点C,即x从小变大时,AD也是先变小再变长,
而△ABC的面积不变,又S=12xy,即y是先变大再变小,
结合选项可知,D选项是正确的;
故选:D.
过点A作AD′⊥BC于点D′,由题可知,当点D从点B运动到点C,即x从小变大时,AD也是先变小再变长,而△ABC的面积不变,又S=12xy,即y是先变大再变小,结合选项可得结论.
本题主要考查动点问题的函数图象,题中没有给任何的数据,需要通过变化趋势进行判断.
7.【答案】B
【解析】
【分析】
本题主要考查了正比例函数的定义,正比例函数y=kx的定义条件是:k为常数,k≠0,自变量次数为1,
根据正比例函数的定义条件进行逐一分析即可.
【解答】
解:(1)y=−x是正比例函数;
(2)y+2=2(x+1),整理得y=2x是正比例函数;
(3)y=k2x(k是常数),当k=0时候,不是正比例函数;
(4)y2=x2,不是正比例函数,
所以有(3)(4)不是正比例函数,总共两个
故选:B.
8.【答案】D
【解析】
【分析】
本题考查一次函数的定义,解题的关键是正确理解一次函数的一般式,本题属于基础题型.形如y=kx+b(k≠0),称为一次函数.
【解答】
解:y=2x+1,y=x+12,s=60t,y=100−25x,
故选D.
9.【答案】A
【解析】
【分析】
本题考查了规律型中的点的坐标的变化,根据点的坐标的变化找出变化规律是解题的关键.设Bn坐标为(xn,yn),根据点B1,B2,B3,B4坐标的变化找出变化规律即可解答.
【解答】
解:设Bn的坐标为(xn,yn),
∵y1=1,y2=2,y3=4,y4=8
∴xn=2n−1,yn=2n−1
∵1=2×1−1,3=2×2−1,7=2×4−1,15=2×8−1
∴xn=2yn−1=2n−1
∴Bn的坐标为(2n−1,2n−1)
故选A.
10.【答案】A
【解析】
【分析】
本题考查一次函数的应用,待定系数法求函数的表达式,两点之间的距离公式,掌握一次函数的性质是解题的关键.
根据题意可求出D点坐标(含a),易求直线AD和OC方程,联立可求E点坐标,通过坐标使OE距离用参数a表示,最终求出OE最短时E点坐标.
【解答】
解:∵D点是BC的中点,B(2,0),C(a,a+6),
∴D(2+a2,a+62),
当a≠0时,由A(−1,0),D(2+a2,a+62),
知kAD=a+622+a2+1=a+6a+4,
∴直线AD方程为y=a+6a+4(x+1),
由于OC过原点,且C(a,a+6),
∴kOC=a+6a,
∴直线OC方程为y=a+6ax,
联立y=a+6a+4(x+1)y=a+6ax,
即a+6ax=a+6a+4(x+1),
得x=a4y=a+64,
∴OE=a42+a+642=a+32+98,
当a=−3时,OE最小,最小值为324,
即E(−34,34);
当a=0时,即D(1,3),
直线AD方程为y=32(x+1),
由于OC在y轴上,
故x=0时,y=32,即E(0,32),
此时OE=32>324,
故当a=−3时,OE最小,此时E(−34,34).
故选A.
11.【答案】C
【解析】
【分析】
本题主要考查一次函数的应用,掌握一次函数图象的意义是解题的关键,特别注意t是小带车所用的时间.
观察图象可判断①②,由图象所给数据可求得小带、小路两车离开A城的距离y与时间t的关系式,可求得两函数图象的交点,可判断③,再令两函数解析式的差为50,可求得t,可判断④,可得出答案.
【解答】
解:由图象可知A、B两城市之间的距离为300km,小带行驶的时间为5小时,而小路是在小带出发1小时后出发的,且用时3小时,即比小带早到1小时,
∴①②都正确;
设小带车离开A城的距离y与t的关系式为y1=kt,
把(5,300)代入可求得k=60,
∴y1=60t,
设小路车离开A城的距离y与t的关系式为y2=mt+n,
把(1,0)和(4,300)代入可得m+n=04m+n=300,
解得:m=100n=−100,
∴y2=100t−100,
令y1=y2,可得:60t=100t−100,
解得:t=2.5,
即小带车、小路车两直线的交点横坐标为t=2.5,
此时小路车出发时间为1.5小时,即小路车出发1.5小时后追上小带车,
∴③不正确;
令|y1−y2|=50,可得|60t−100t+100|=50,即|100−40t|=50,
当100−40t=50时,可解得t=54,
当100−40t=−50时,可解得t=154,
又当t=56时,y1=50,此时小路车还没出发,
当t=256时,小路车到达B城,y1=250;
综上可知当t的值为54或154或56或256时,两车相距50千米,
∴④不正确;
故选C.
12.【答案】B
【解析】
【分析】
本题主要考查一次函数的应用,掌握一次函数图象的意义是解题的关键,特别注意t是甲车所用的时间.观察图象可判断①②,由图象所给数据可求得甲、乙两车离开A城的距离y与时间t的关系式,可求得两函数图象的交点,可判断③,再令两函数解析式的差为50,可求得t,可判断④,可得出答案.
【解答】
解:由图象可知A、B两城市之间的距离为300km,甲行驶的时间为5小时,而乙是在甲出发1小时后出发的,且用时3小时,即比甲早到1小时,
∴①②都正确;
设甲车离开A城的距离y与t的关系式为y甲=kt,
把(5,300)代入可求得k=60,
∴y甲=60t,
设乙车离开A城的距离y与t的关系式为y乙=mt+n,
把(1,0)和(4,300)代入可得m+n=04m+n=300,解得m=100n=−100,
∴y乙=100t−100,
令y甲=y乙可得:60t=100t−100,解得t=2.5,
即甲、乙两直线的交点横坐标为t=2.5,
此时乙出发时间为1.5小时,即乙车出发1.5小时后追上甲车,
∴③不正确;
令|y甲−y乙|=50,可得|60t−100t+100|=50,即|100−40t|=50,
当100−40t=50时,可解得t=54,
当100−40t=−50时,可解得t=154,
又当t=56时,y甲=50,此时乙还没出发,
当t=256时,乙到达B城,y甲=250;
综上可知当t的值为54或154或56或t=256时,两车相距50千米,
∴④不正确;
综上可知正确的有①②共两个,
故选:B.
13.【答案】1380
【解析】
【分析】
本题考查了用图象表示变量之间的关系,根据“速度=路程÷时间”结合图象即可算出乙的速度,再根据“甲的速度=乙的速度+两者速度差”即可求出甲的速度,进而即可求出甲、乙会合地离起点的距离,结合总路程及二者的速度即可得出甲到终点时,乙离起点的距离,此题得解.
【解答】
解:由题意,知乙的速度为1800÷1200=1.5(米/秒).
甲的速度为1.5+300÷300=2.5(米/秒).
∴两人相距300米时,甲跑的路程是2.5×300=750(米),此时离终点的距离为1800−750=1050(米).
∴从会合到终点,甲所用时间是1050÷2.5=420(秒),乙从会合点跑420秒的路程是420×1.5=630(米).
∴当甲到达终点时,乙跑的总路程是750+630=1380(米)
故答案为1380.
14.【答案】30−14x
【解析】解:由题意,得
每天修30÷120=14km,
y=30−14x,
故答案为:30−14x.
根据总工程量减去已修的工程量,可得答案.
本题考查了函数关系式,利用总工程量减去已修的工程量是解题关键.
15.【答案】3
【解析】
【分析】
此题主要考查了一次函数的定义,一次函数y=kx+b的定义条件是:k、b为常数,k≠0,自变量次数为1.根据一次函数定义可得m−2=1,再解方程即可得到m的值.
【解答】
解:由题意得:m−2=1,
解得:m=3,
故答案为3.
16.【答案】表示每小时平均耗油7.5升
【解析】
【分析】
本题主要考查的是一次函数的图象和应用的有关知识,又经过2小时,汽车油箱剩余油量10升,即每小时耗油(25−10)÷2=7.5升,进而解出此题的答案.
【解答】
解:函数y=−7.5t+25中,t的系数−7.5表示的实际意义是表示每小时平均耗油7.5升.
故答案为表示每小时平均耗油7.5升.
17.【答案】解:(1)900
(2)图中点B的实际意义:当行驶4h时,慢车和快车相遇.
(3)由图象可知,慢车12h行驶的路程为900km,
所以慢车的速度为90012=75(km/h).
当慢车行驶4h时,慢车和快车相遇,两车行驶的路程之和为900km,
所以慢车和快车行驶的速度之和为9004=225(km/h),
所以快车的速度为225−75=150(km/h).
【解析】见答案.
18.【答案】(1)420;140;70;
(2)143;
(3)97或197或417.
【解析】
【分析】
本题考查了用图像表示变量之间的关系,主要利用了时间、路程、速度三者之间的关系和追击问题的等量关系,难点在于(2)表示出快车距离出发地的路程.
(1)先得两地的距离,根据速度=路程÷时间列式计算即可求出快车和慢车的速度;
(2)根据两车的速度等条件可得出答案;
(3)分别根据两车相遇前、两车相遇后以及快车从乙往甲返回途中,三种情况两车距离为150km时,列方程可解答.
【解答】
解:(1)由图可知:甲乙两地之间的路程为420km;
快车的速度为:4204−1=140km/h;
由题意得:快车7小时到达甲地,则慢车6小时到达甲地,
则慢车的速度为:4206=70km/h;
故答案为:420,140,70;
(2)设经过t小时后,快、慢两车距各自出发地的路程相等,
则70t=140(7−t)
解得:t=143,
答:出发143小时,快、慢两车距各自出发地的路程相等;
故答案为:143;
(3)第一种情形第一次没有相遇前,相距150km,
则140x+70x+150=420,
解得:x=97,
第二种情形应是相遇后而快车没到乙地前140x+70x−420=150,
解得:x=197,
第三种情形是快车从乙往甲返回途中:70x−140(x−4)=150,
解得:x=417,
综上所述:快慢两车出发97h或197h或417h相距150km.
故答案为:97或197或417.
19.【答案】解:(1)∵点C的坐标为(2,8),点A的坐标为(26,0),
∴OA=26,BC=24,AB=8,
∵D(E)点运动的时间为t秒,
∴BD=t,OE=3t,
当BD=AE时,四边形ABDE是矩形,
即t=26−3t,
解得,t=132;
(2)由题意得CD=24−t,
①四边形OEDC为平行四边形时,DE=OC,
即24−t=3t,
解得,t=6;
②四边形OEDC为等腰梯形时,若DE=CO,则CD+4=OE,
即24−t+4=3t,解得,t=7;
③当E在AB上时,BE=34−3t,BD=t,DE=OC=22+82=68,
∴在Rt△BDE中,BD2+BE2=DE2,
即t2+(34−3t)2=68,化简得:5t2−102t+544=0,
∵Δ=1022−4×5×544=−476<0,
∴原方程无实数根;
综上所述:当t=6或t=7时,DE=CO.
(3)如图1,当点E在OA上时,
AE=26−3t,
则S=12×AE×AB=12×(26−3t)×8=−12t+104,
当点E在AB上时,AE=3t−26,BD=t,
则S=12×AE×DB=12×(3t−26)×t=32t2−13t.
【解析】本题考查的是矩形的判定、平行四边形的判定和性质以及函数解析式的确定,掌握相关的性质定理和判定定理、灵活运用分情况讨论思想是解题的关键.
(1)根据矩形的判定定理列出关系式,计算即可;
(2)根据平行四边形的判定定理和性质、等腰梯形的性质以及勾股定理定理分情况解答;
(3)分点E在OA上和点E在AB上两种情况,根据三角形的面积公式计算即可.
20.【答案】 解:(1)210÷(9−6)=70(千米/时),
答:该团去景点时的平均速度是70千米/时;
(2)由横坐标得出9时到达景点,13是离开景点,13−9=4小时,
答:该团在旅游景点游玩了4小时;
(3)设返回途中函数关系式是S=kt+b,由题意,得
13t+b=21015t+b=110,
解得k=−50t=860,
返回途中函数关系式是S=−50t+860,
当s=0时,t=17.2,
返回到宾馆的时刻是17点12分.
【解析】本题考查了函数图象,观察函数图象得出路程与时间的关系是解题关键.
(1)根据路程除以时间等于速度,可得答案;
(2)根据路程不变,可得相应的自变量的范围;
(3)根据待定系数法,可得函数关系式,根据自变量与函数值得对应关系,可得答案.
21.【答案】解:(1)3;
(2)根据定义得:
y1: y=x+2,x≤1 y=−x−2,x>1,y2: y=− 1 2x−2,x≥−1 y= 1 2 x+2,x>−1,
求交点坐标:① y=x+2,x≤1 y=− 1 2 x−2,x≤−1,解得−83y=−23;
②y=x+2,x≤1 y= 1 2x+2,x>−1解得: x=0 y=2;
① y=−x−2,x>1 y=− 12 x−2,x≤−1,无解;
② y=−x−2,x>1 y= 12 x+2,x>−1,无解;
综上所述函数y1和函数y2的交点坐标为(−83,−23)和(0,2);
(3)①−8≤y1≤4;
②−2≤m<−25.
【解析】
【分析】
本题考查一次函数的应用、两直线平行或相交等知识,解题的关键是理解题意,学会构建方程组确定两个函数的交点坐标,属于中考压轴题.
(1)根据m变函数的定义即可解决问题;
(2)转化为方程组解决问题即可;
(3)①根据m变函数的定义,求出特殊点的函数值即可解决问题;
②利用方程组求出交点坐标即可解决问题;
【解答】
解:(1)根据m变函数定义,关于x的一次函数y=−x+1的2变函数为:
y=−x+1x≤2 y=x−1x>2,
∴x=4时,y=4−1=3,
故答案为3;
(2)见答案;
(3)①由题意:y1: y=2x+2,x≤1 y=−2x−2,x>1,
∴x=−3时,y=−4,x=3时,y=−8,
x=1时,y=4,
∴−8≤y1≤4
故答案为−8≤y1≤4;
②由题意:y1: y=2x+2,x≤1 y=−2x−2,x>1,y2: y= 12 x−1,x≤m y=− 12 x+1,x>m,
易知两个函数的交点(−2,−2),(−25,65),
观察图象可知:−2≤m<−25时,函数y1和函数y2有且仅有两个交点.
故答案为−2≤m<−25.
22.【答案】解:(1)把x=0代入y=kx−3得y=−3,
所以B点坐标为(0,−3);
(2)∵△OAB(O为坐标原点)的面积为4,
∴12OA⋅3=4,
∴OA=83,
∵函数y的值随x的增大而增大,
∴点A的坐标为(83,0),
把点A的坐标为(83,0)代入y=kx−3得,
83k−3=0,
解得:k=98.
【解析】本题考查了一次函数的性质,三角形的面积的有关知识.
(1)根据y轴上点的坐标特征,求自变量为0时的函数值即可得到B点坐标;
(2)根据三角形面积公式得到OA=83,再利用一次函数的性质得点A的坐标为(83,0),然后把A点坐标代入y=kx−3即可计算出k的值.
23.【答案】解:(1)如图1,过点C作CD⊥x轴于点D,
对于一次函数y=14x+1,
令x=0,则y=1;
令y=0,则14x+1=0,即x=−4,故B0,1,A−4,0,
∴OA=4,OB=1,
∵∠ADC=∠BOA=90°,
∴∠CAD+∠ACD=90°,
∵∠BAC=90°,
∴∠CAD+∠BAO=90°,
∴∠ACD=∠BAO,
∵△ABC是等腰直角三角形,
∴AC=AB,
在△ADC和△BOA中,
∠ADC=∠BOA,∠ACD=∠BAO,AC=BA,
∴△ADC≌△BOA(AAS),
∴CD=OA=4,AD=BO=1,
∴OD=OA+AD=5,
∴C(−5,4);
(2)存在点E,使得|EC−EB|的值最大.
∵E是x轴上的一个动点,
∴|EC−EB|≤BC,
∴当点E在CB的延长线与x轴的交点上时,|EC−EB|=BC,此时|EC−EB|的值最大,
如图2,延长CB交x轴于点E,设直线CB的解析式为y=kx+b,
∵B(0,1),C(−5,4),
∴b=1,−5k+b=4,解得k=−35,b=1,
∴直线CB的解析式为y=−35x+1.
当y=0时,−35x+1=0,解得x=53,
∴E(53,0);
(3)点Q的坐标为(−3,−4),(−1,5),(1,−3).
【解析】本题主要考查一次函数与等腰直角三角形的综合,用待定系数法确定函数的解析式,一次函数图象的性质,一次函数图象上点的坐标的特征,全等三角形的判定与性质等知识,利用点的坐标表示出相应线段的长度是解题的关键,注意分类讨论.
(1)过点C作CD⊥x轴于点D,通过证明△ADC≌△BOA,求得线段OD,CD的长度即可得出结论;
(2)延长CB,交x轴于点E,则此时|EC−EB|的值最大,利用待定系数法求得直线BC的解析式,令y=0即可求得点E的横坐标;
(3)分三种情况,分别过点Q作x、y轴的垂线,通过全等三角形的性质求出点Q到x、y轴的垂线段的长,即得点Q的坐标.
解:(3)如图3,△ABC≌△ABQ1≌△BAQ2≌△BAQ3,过点Q1作Q1F⊥x轴于点F,
过点Q2作Q2G⊥y轴于点G,过点Q3作Q3H⊥y轴于点H,
易证△ABO≌△Q1AF≌△BQ2G≌△BQ3H,
∴OA=FQ1=GB=HB,OB=FA=GQ2=HQ3,
由(1)可知OA=4,OB=1,
∴OA=FQ1=GB=HB=4,OB=FA=GQ2=HQ3=1,
∴Q1(−3,−4),Q2(−1,5),Q3(1,−3),
综上所述,点Q的坐标为(−3,−4),(−1,5),(1,−3),
故答案为:Q的坐标为(−3,−4),(−1,5),(1,−3).
24.【答案】解:(1)设组装A型、B型、C型玩具的技工分别为x、y、(20−x−y)名.
根据题意得22x+21y+20(20−x−y)=420.
整理得y=−2x+20,
∵20−x−y=20−x−(−2x+20)=x,
∴组装A型、B型、C型玩具的技工分别为x、(−2x+20)、x名
由题意可知x≥2−2x+20≥2,x≥2,解得2≤x≤9,且x是整数,
(2)由题意可知:W=8×22x+10×21(−2x+20)+6×20x.
即W=−124x+4200(W是x的一次函数)
∵k=−124<0,
∴W随x的增大而减小
∵2≤x≤9,且x是整数
∴当x=2时,W的值最大.
此时W=3952(元),即最大利润为3952元.
生产分配方案如下:组装A型玩具2人,B型玩具16人,C型玩具2人.
【解析】(1)设组装A型、B型、C型玩具的技工分别为x、y、(20−x−y)人,然后根据玩具总个数为420,列出等式,然后整理即可得到y与x的函数关系式,然后根据至少有2名技工组装同一个型号的玩具列不等式组求解即可;
(2)然后根据总利润=三种类型玩具的利润和;每种玩具的利润=玩具数量×每个玩具的利润列出函数关系式,然后根据关系进行判断即可.
本题主要考查的是一次函数的应用,根据一次函数的性质判断出W取得最大值是x的取值是解题的关键.
25.【答案】解:由题意得,甲店B型产品有(70−x)件,乙店A型有(40−x)件,B型有(x−10)件,
则(1)W=200x+170(70−x)+160(40−x)+150(x−10)=20x+16800.
由x≥070−x≥040−x≥0x−10≥0,
解得10≤x≤40;
(2)由W=20x+16800≥17560,
解得x≥38.
故38≤x≤40,x=38,39,40.
则有三种不同的分配方案.
①x=38时,甲店A型38件,B型32件,乙店A型2件,B型28件;
②x=39时,甲店A型39件,B型31件,乙店A型1件,B型29件;
③x=40时,甲店A型40件,B型30件,乙店A型0件,B型30件;
(3)依题意:W=(200−a)x+170(70−x)+160(40−x)+150(x−10)=(20−a)x+16800.
①当0
③当20
(2)让(1)中的代数式≥17560,结合(1)中自变量的取值可得相应的分配方案;
(3)根据让利后A型产品的每件利润仍高于甲店B型产品的每件利润可得a的取值,结合(1)得到相应的总利润,根据a的不同取值得到利润的函数应得到的最大值的方案即可.
此题主要考查了一次函数的应用;得到分配给甲乙两店的不同型号的产品的数量是解决本题的突破点;得到总利润的关系式是解决本题的关键;根据a的不同取值得到相应的最大利润是解决本题的难点.
浙教版初中数学八年级上册期末测试卷(困难)(含答案解析): 这是一份浙教版初中数学八年级上册期末测试卷(困难)(含答案解析),共22页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
浙教版初中数学八年级上册期中测试卷(困难)(含答案解析): 这是一份浙教版初中数学八年级上册期中测试卷(困难)(含答案解析),共25页。试卷主要包含了二章等内容,欢迎下载使用。
浙教版初中数学八年级上册期末测试卷(困难)(含答案解析): 这是一份浙教版初中数学八年级上册期末测试卷(困难)(含答案解析),共32页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。