(新高考)高考数学一轮复习讲与练第8章§8.2《两条直线的位置关系》(含详解)

这是一份(新高考)高考数学一轮复习讲与练第8章§8.2《两条直线的位置关系》(含详解)，共15页。试卷主要包含了三种距离公式，故选C，))等内容，欢迎下载使用。

知识梳理
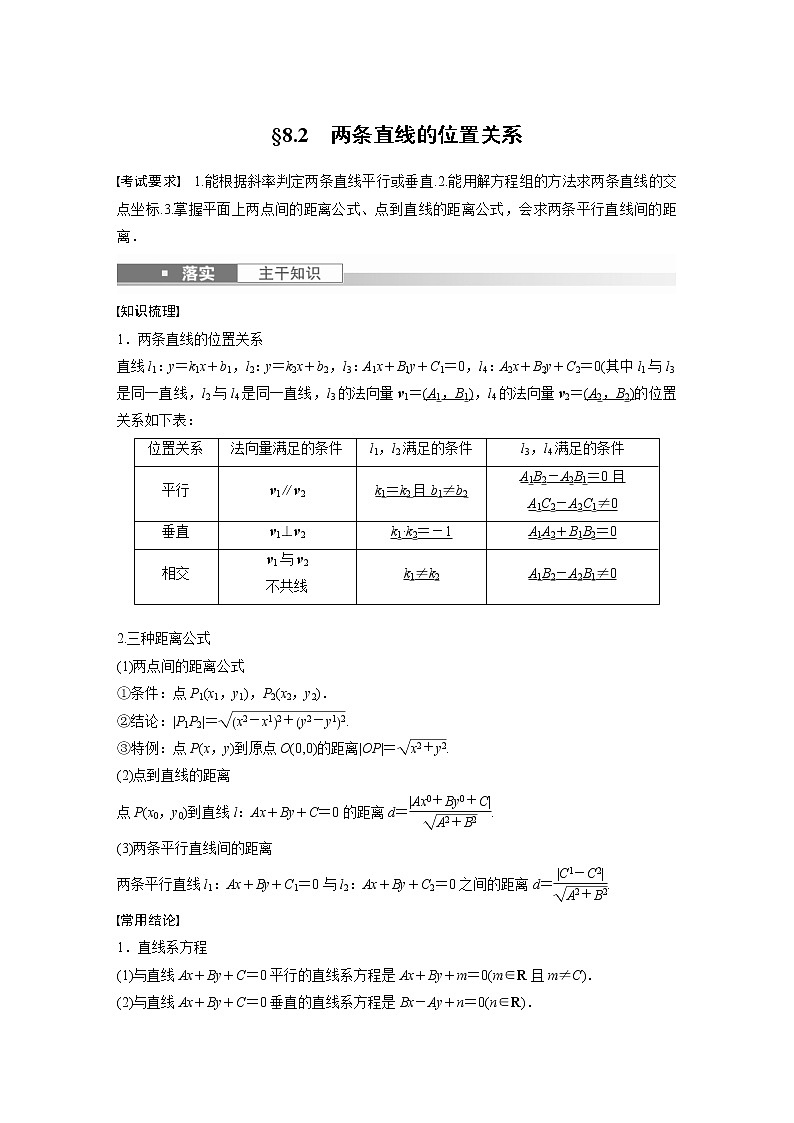
1．两条直线的位置关系
直线l1：y＝k1x＋b1，l2：y＝k2x＋b2，l3：A1x＋B1y＋C1＝0，l4：A2x＋B2y＋C2＝0(其中l1与l3是同一直线，l2与l4是同一直线，l3的法向量v1＝(A1，B1)，l4的法向量v2＝(A2，B2)的位置关系如下表：
2.三种距离公式
(1)两点间的距离公式
①条件：点P1(x1，y1)，P2(x2，y2)．
②结论：|P1P2|＝eq \r(x2－x12＋y2－y12).
③特例：点P(x，y)到原点O(0,0)的距离|OP|＝eq \r(x2＋y2).
(2)点到直线的距离
点P(x0，y0)到直线l：Ax＋By＋C＝0的距离d＝eq \f(|Ax0＋By0＋C|,\r(A2＋B2)).
(3)两条平行直线间的距离
两条平行直线l1：Ax＋By＋C1＝0与l2：Ax＋By＋C2＝0之间的距离d＝eq \f(|C1－C2|,\r(A2＋B2)).
常用结论
1．直线系方程
(1)与直线Ax＋By＋C＝0平行的直线系方程是Ax＋By＋m＝0(m∈R且m≠C)．
(2)与直线Ax＋By＋C＝0垂直的直线系方程是Bx－Ay＋n＝0(n∈R)．
(3)过直线l1：A1x＋B1y＋C1＝0与l2：A2x＋B2y＋C2＝0的交点的直线系方程为A1x＋B1y＋C1＋λ(A2x＋B2y＋C2)＝0(λ∈R)，但不包括l2.
2．五种常用对称关系
(1)点(x，y)关于原点(0,0)的对称点为(－x，－y)．
(2)点(x，y)关于x轴的对称点为(x，－y)，关于y轴的对称点为(－x，y)．
(3)点(x，y)关于直线y＝x的对称点为(y，x)，关于直线y＝－x的对称点为(－y，－x)．
(4)点(x，y)关于直线x＝a的对称点为(2a－x，y)，关于直线y＝b的对称点为(x，2b－y)．
(5)点(x，y)关于点(a，b)的对称点为(2a－x，2b－y)．
思考辨析
判断下列结论是否正确(请在括号中打“√”或“×”)
(1)当直线l1和l2斜率都存在时，一定有k1＝k2⇒l1∥l2.( × )
(2)若两直线的方程组成的方程组有解，则两直线相交．( × )
(3)点P(x0，y0)到直线y＝kx＋b的距离为eq \f(|kx0＋b|,\r(1＋k2)).( × )
(4)直线外一点与直线上点的距离的最小值就是点到直线的距离．( √ )
教材改编题
1．点A(2,5)到直线l：x－2y＋3＝0的距离为( )
A．2eq \r(5) B.eq \f(\r(5),5)
C.eq \r(5) D.eq \f(2\r(5),5)
答案 C
解析 点A(2,5)到直线l：x－2y＋3＝0的距离为d＝eq \f(|2－10＋3|,\r(1＋4))＝eq \r(5).
2．直线2x＋(m＋1)y＋4＝0与直线mx＋3y－2＝0平行，则m等于( )
A．2 B．－3
C．2或－3 D．－2或－3
答案 C
解析 直线2x＋(m＋1)y＋4＝0与直线mx＋3y－2＝0平行，则有eq \f(2,m)＝eq \f(m＋1,3)≠eq \f(4,－2)(m≠0)，故m＝2或－3.故选C.
3．直线l1：2x＋y－1＝0和l2：x－2y＋7＝0的交点的坐标为________．
答案 (－1,3)
解析 解方程组eq \b\lc\{\rc\ (\a\vs4\al\c1(2x＋y－1＝0，,x－2y＋7＝0，))得eq \b\lc\{\rc\ (\a\vs4\al\c1(x＝－1，,y＝3，))
所以两条直线交点的坐标为(－1,3).
题型一 两条直线的平行与垂直
例1 (1)(2022·杭州模拟)已知直线l1：ax＋(a＋2)y＋1＝0，l2：x＋ay＋2＝0(a∈R)，则“ea＝eq \f(1,e)”是“l1∥l2”的( )
A．充分不必要条件
B．必要不充分条件
C．充要条件
D．既不充分也不必要条件
答案 A
解析 当l1∥l2时，eq \b\lc\{\rc\ (\a\vs4\al\c1(a2－a＋2＝0，,2a－1≠0，))
解得a＝－1或a＝2.
而由ea＝eq \f(1,e)，解得a＝－1，
所以“ea＝eq \f(1,e)”是“l1∥l2”的充分不必要条件．
(2)(2022·长春模拟)已知直线l经过点(1，－1)，且与直线2x－y－5＝0垂直，则直线l的方程为( )
A．2x＋y－1＝0 B．x－2y－3＝0
C．x＋2y＋1＝0 D．2x－y－3＝0
答案 C
解析 ∵直线l与直线2x－y－5＝0垂直，
∴设直线l的方程为x＋2y＋c＝0，
∵直线l经过点(1，－1)，
∴1－2＋c＝0，即c＝1.
直线l的方程为x＋2y＋1＝0.
教师备选
1．“m＝3”是“直线l1：2(m＋1)x＋(m－3)y＋7－5m＝0与直线l2：(m－3)x＋2y－5＝0垂直”的( )
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件
答案 A
解析 由l1⊥l2，得2(m＋1)(m－3)＋2(m－3)＝0，
∴m＝3或m＝－2，
∴“m＝3”是“l1⊥l2”的充分不必要条件．
2．已知三条直线2x－3y＋1＝0,4x＋3y＋5＝0，mx－y－1＝0不能构成三角形，则实数m的取值集合为( )
A.eq \b\lc\{\rc\}(\a\vs4\al\c1(－\f(4,3)，\f(2,3))) B.eq \b\lc\{\rc\}(\a\vs4\al\c1(－\f(4,3)，\f(2,3)，\f(4,3)))
C.eq \b\lc\{\rc\}(\a\vs4\al\c1(\f(4,3)，－\f(2,3))) D.eq \b\lc\{\rc\}(\a\vs4\al\c1(－\f(4,3)，－\f(2,3)，\f(2,3)))
答案 D
解析 由题意得直线mx－y－1＝0与2x－3y＋1＝0或4x＋3y＋5＝0平行，或者直线mx－y－1＝0过2x－3y＋1＝0与4x＋3y＋5＝0的交点．当直线mx－y－1＝0与2x－3y＋1＝0或4x＋3y＋5＝0平行时，m＝eq \f(2,3)或m＝－eq \f(4,3)；当直线mx－y－1＝0过2x－3y＋1＝0与4x＋3y＋5＝0的交点时，m＝－eq \f(2,3).所以实数m的取值集合为eq \b\lc\{\rc\}(\a\vs4\al\c1(－\f(4,3)，－\f(2,3)，\f(2,3))).
思维升华 判断两条直线位置关系的注意点
(1)斜率不存在的特殊情况．
(2)可直接利用直线方程系数间的关系得出结论．
跟踪训练1 (1)(2022·荆门模拟)数学家欧拉在1765年提出定理：三角形的外心、重心、垂心依次位于同一直线上，且重心到外心的距离是重心到垂心距离的一半．这条直线被后人称为三角形的欧拉线，已知△ABC的顶点A(2,0)，B(1,2)，且AC＝BC，则△ABC的欧拉线的方程为( )
A．x－2y－4＝0 B．2x＋y－4＝0
C．4x＋2y＋1＝0 D．2x－4y＋1＝0
答案 D
解析 由题设，可得kAB＝eq \f(2－0,1－2)＝－2，
且AB的中点为eq \b\lc\(\rc\)(\a\vs4\al\c1(\f(3,2)，1))，
∴AB垂直平分线的斜率k＝－eq \f(1,kAB)＝eq \f(1,2)，
故AB的垂直平分线方程为y＝eq \f(1,2)eq \b\lc\(\rc\)(\a\vs4\al\c1(x－\f(3,2)))＋1＝eq \f(x,2)＋eq \f(1,4)，
∵AC＝BC，则△ABC的外心、重心、垂心都在AB的垂直平分线上，
∴△ABC的欧拉线的方程为2x－4y＋1＝0.
(2)已知两直线l1：x＋ysin α＋1＝0和l2：2xsin α＋y＋1＝0.若l1∥l2，则α＝________.
答案 kπ±eq \f(π,4)，k∈Z
解析 由A1B2－A2B1＝0，得1－2sin2α＝0，
所以sin α＝±eq \f(\r(2),2).
又A1C2－A2C1≠0，
所以1－2sin α≠0，即sin α≠eq \f(1,2).
所以α＝kπ±eq \f(π,4)，k∈Z.
故当α＝kπ±eq \f(π,4)，k∈Z时，l1∥l2.
题型二 两直线的交点与距离问题
例2 (1)两条平行直线2x－y＋3＝0和ax＋3y－4＝0间的距离为d，则a，d的值分别为( )
A．a＝6，d＝eq \f(\r(6),3) B．a＝－6，d＝eq \f(\r(5),3)
C．a＝6，d＝eq \f(\r(5),3) D．a＝－6，d＝eq \f(\r(6),3)
答案 B
解析 由题知2×3＝－a，解得a＝－6，
又－6x＋3y－4＝0可化为2x－y＋eq \f(4,3)＝0，
∴d＝eq \f(\b\lc\|\rc\|(\a\vs4\al\c1(3－\f(4,3))),\r(5))＝eq \f(\r(5),3).
(2)已知直线经过点(1,2)，并且与点(2,3)和(0，－5)的距离相等，则此直线的方程为________________．
答案 4x－y－2＝0或x＝1
解析 若所求直线的斜率存在，则可设其方程为y－2＝k(x－1)，即kx－y－k＋2＝0，
由题设有eq \f(|2k－3－k＋2|,\r(1＋k2))＝eq \f(|0＋5－k＋2|,\r(1＋k2))，
即|k－1|＝|7－k|，解得k＝4.
此时直线方程为4x－y－2＝0.
若所求直线的斜率不存在，则直线方程为x＝1，满足题设条件．
故所求直线的方程为4x－y－2＝0或x＝1.
教师备选
1．经过两直线l1：x－2y＋4＝0和l2：x＋y－2＝0的交点P，且与直线l3：3x－4y＋5＝0垂直的直线l的方程为________．
答案 4x＋3y－6＝0
解析 由方程组eq \b\lc\{\rc\ (\a\vs4\al\c1(x－2y＋4＝0，,x＋y－2＝0，))得eq \b\lc\{\rc\ (\a\vs4\al\c1(x＝0，,y＝2，))
即P(0,2)．
因为l⊥l3，所以直线l的斜率k＝－eq \f(4,3)，
所以直线l的方程为y－2＝－eq \f(4,3)x，
即4x＋3y－6＝0.
2．直线l1经过点(3,0)，直线l2经过点(0,4)，且l1∥l2，d表示l1和l2之间的距离，则d的取值范围是________．
答案 (0,5]
解析 当直线l1，l2都与过(3,0)，(0,4)两点的直线垂直时，
dmax＝eq \r(32＋42)＝5；
当直线l1和l2都经过(3,0)，(0,4)两点时，两条直线重合．
所以0＜d≤5.
思维升华 利用距离公式应注意的点
(1)点P(x0，y0)到直线x＝a的距离d＝|x0－a|，到直线y＝b的距离d＝|y0－b|.
(2)两条平行线间的距离公式要把两条直线方程中x，y的系数化为相等．
跟踪训练2 (1)若P，Q分别为直线3x＋4y－12＝0与6x＋8y＋5＝0上任意一点，则|PQ|的最小值为( )
A.eq \f(9,5) B.eq \f(18,5)
C.eq \f(29,10) D.eq \f(29,5)
答案 C
解析 因为eq \f(3,6)＝eq \f(4,8)≠eq \f(－12,5)，所以两直线平行，将直线3x＋4y－12＝0化为6x＋8y－24＝0，由题意可知|PQ|的最小值为这两条平行直线间的距离，即eq \f(|－24－5|,\r(62＋82))＝eq \f(29,10)，
所以|PQ|的最小值为eq \f(29,10).
(2)点(0，－1)到直线y＝k(x＋1)距离的最大值为( )
A．1 B.eq \r(2) C.eq \r(3) D．2
答案 B
解析 由y＝k(x＋1)可知直线过定点P(－1,0)，设A(0，－1)，当直线y＝k(x＋1)与AP垂直时，点A到直线y＝k(x＋1)的距离最大，即为|AP|＝eq \r(2).
题型三 对称问题
命题点1 点关于点中心对称
例3 过点P(0,1)作直线l，使它被直线l1：2x＋y－8＝0和l2：x－3y＋10＝0截得的线段被点P平分，则直线l的方程为________________．
答案 x＋4y－4＝0
解析 设l1与l的交点为A(a，8－2a)，则由题意知，点A关于点P的对称点B(－a，2a－6)在l2上，代入l2的方程得－a－3(2a－6)＋10＝0，解得a＝4，即点A(4,0)在直线l上，所以直线l的方程为x＋4y－4＝0.
命题点2 点关于直线对称
例4 若将一张坐标纸折叠一次，使得点(0,2)与点(4,0)重合，点(7,3)与点(m，n)重合，则m＋n＝________.
答案 eq \f(34,5)
解析 由题可知纸的折痕应是点(0,2)与点(4,0)连线的垂直平分线，即直线y＝2x－3，它也是点(7,3)与点(m，n)连线的垂直平分线，
于是eq \b\lc\{\rc\ (\a\vs4\al\c1(\f(3＋n,2)＝2×\f(7＋m,2)－3，,\f(n－3,m－7)＝－\f(1,2)，))
解得eq \b\lc\{\rc\ (\a\vs4\al\c1(m＝\f(3,5)，,n＝\f(31,5)，))故m＋n＝eq \f(34,5).
命题点3 线关于线对称
例5 直线2x－4y－1＝0关于x＋y＝0对称的直线方程为( )
A．4x－2y－1＝0 B．4x－2y＋1＝0
C．4x＋2y＋1＝0 D．4x＋2y－1＝0
答案 A
解析 设直线2x－4y－1＝0上一点P(x0，y0)关于直线x＋y＝0对称的点的坐标为P′(x，y)，
则eq \b\lc\{\rc\ (\a\vs4\al\c1(\f(y－y0,x－x0)＝1，,\f(x＋x0,2)＋\f(y＋y0,2)＝0，))
整理可得eq \b\lc\{\rc\ (\a\vs4\al\c1(x0＝－y，,y0＝－x，))
∴－2y＋4x－1＝0，
即直线2x－4y－1＝0关于x＋y＝0对称的直线方程为4x－2y－1＝0.
教师备选
1．在等腰直角三角形ABC中，AB＝AC＝4，点P是边AB上异于A，B的一点．光线从点P出发，经BC，CA反射后又回到点P(如图所示)．若光线QR经过△ABC的重心，则AP的长度为( )
A．2 B．1 C.eq \f(8,3) D.eq \f(4,3)
答案 D
解析 以A为原点，AB所在直线为x轴，AC所在直线为y轴，建立如图所示的平面直角坐标系，由题意可知B(4,0)，C(0,4)，A(0,0)，则直线BC的方程为x＋y－4＝0.设P(t，0)(00)，
则f′(x0)＝1－eq \f(1,x\\al(2,0))，点P与直线3x－4y－2＝0的最小距离，即为点P处的切线的斜率等于直线3x－4y－2＝0的斜率时的情况，即满足1－eq \f(1,x\\al(2,0))＝eq \f(3,4)，
解得x0＝2，
所以y0＝2＋eq \f(1,2)＝eq \f(5,2)，
所以点Peq \b\lc\(\rc\)(\a\vs4\al\c1(2，\f(5,2)))，
所以点P到直线3x－4y－2＝0的距离的最小值为d＝eq \f(\b\lc\|\rc\|(\a\vs4\al\c1(2×3－4×\f(5,2)－2)),\r(42＋32))＝eq \f(6,5)，
故只需满足d≥eq \f(6,5)即可．
15．(多选)定义点P(x0，y0)到直线l：ax＋by＋c＝0(a2＋b2≠0)的有向距离为d＝eq \f(ax0＋by0＋c,\r(a2＋b2)).已知点P1，P2到直线l的有向距离分别是d1，d2.以下命题不正确的是( )
A．若d1＝d2＝1，则直线P1P2与直线l平行
B．若d1＝1，d2＝－1，则直线P1P2与直线l垂直
C．若d1＋d2＝0，则直线P1P2与直线l垂直
D．若d1·d2≤0，则直线P1P2与直线l相交
答案 BCD
解析 设P1(x1，y1)，P2(x2，y2)，
对于A，若d1＝d2＝1，
则ax1＋by1＋c＝ax2＋by2＋c＝eq \r(a2＋b2)，直线P1P2与直线l平行，正确；
对于B，点P1，P2在直线l的两侧且到直线l的距离相等，直线P1P2不一定与l垂直，错误；
对于C，若d1＝d2＝0，满足d1＋d2＝0，
即ax1＋by1＋c＝ax2＋by2＋c＝0，
则点P1，P2都在直线l上，所以此时直线P1P2与直线l重合，错误；
对于D，若d1·d2≤0，
即(ax1＋by1＋c)(ax2＋by2＋c)≤0，
所以点P1，P2分别位于直线l的两侧或在直线l上，
所以直线P1P2与直线l相交或重合，错误．
16．(多选)(2022·武汉调研)台球运动已有五、六百年的历史，参与者用球杆在台上击球．若和光线一样，台球在球台上碰到障碍物后也遵从反射定律．如图，有一张长方形球台ABCD，AB＝2AD，现从角落A沿角α的方向把球打出去，球经2次碰撞球台内沿后进入角落C的球袋中，则tan α的值可能为( )
A.eq \f(1,6) B.eq \f(1,2) C．1 D.eq \f(3,2)
答案 AD
解析 如图1，A关于DC的对称点为E，D关于AB的对称点为G，C关于AB的对称点为F，连接GF，EF，
由题可得tan α＝eq \f(EG,GF)＝eq \f(3AD,2AD)＝eq \f(3,2).

图1 图2
如图2，A关于BC的对称点为G，B关于AD的对称点为F，C关于AD的对称点为E，连接EF，EG，
由题可得tan α＝eq \f(EF,GF)＝eq \f(AD,6AD)＝eq \f(1,6).位置关系
法向量满足的条件
l1，l2满足的条件
l3，l4满足的条件
平行
v1∥v2
k1＝k2且b1≠b2
A1B2－A2B1＝0且
A1C2－A2C1≠0
垂直
v1⊥v2
k1·k2＝－1
A1A2＋B1B2＝0
相交
v1与v2
不共线
k1≠k2
A1B2－A2B1≠0