

(新高考)高考数学一轮复习课时练习1.2《充分条件与必要条件、全称量词与存在量词》(含解析)
展开
这是一份(新高考)高考数学一轮复习课时练习1.2《充分条件与必要条件、全称量词与存在量词》(含解析),共14页。试卷主要包含了全称命题和特称命题,对充分必要条件判断不明致误,已知p,下列说法正确的是等内容,欢迎下载使用。
第2讲 充分条件与必要条件、全称量词与存在量词
最新考纲
考向预测
1.理解必要条件、充分条件与充要条件的意义.
2.理解全称量词与存在量词的意义,能正确地对含有一个量词的命题进行否定.
命题
趋势
含有一个量词的命题的否定和充分必要条件的判定是高考的重点,一般多与集合、函数、不等式、立体几何结合,考查考生的推理能力,考查形式以基础题为主,低档难度.
核心
素养
逻辑推理、数学抽象
1.充分条件、必要条件与充要条件的概念
若p⇒q,则p是q的充分条件,q是p的必要条件
p是q的充分不必要条件
p⇒q且qp
p是q的必要不充分条件
pq且q⇒p
p是q的充要条件
p⇔q
p是q的既不充分也不必要条件
pq且qp
[注意] 不能将“若p,则q”与“p⇒q”混为一谈,只有“若p,则q”为真命题时,才有“p⇒q”,即“p⇒q”⇔“若p,则q”为真命题.
2.全称命题和特称命题
(1)全称量词和存在量词
量词名称
常见量词
符号表示
全称量词
所有、一切、任意、全部、每一个等
∀
存在量词
存在一个、至少有一个、有些、某些等
∃
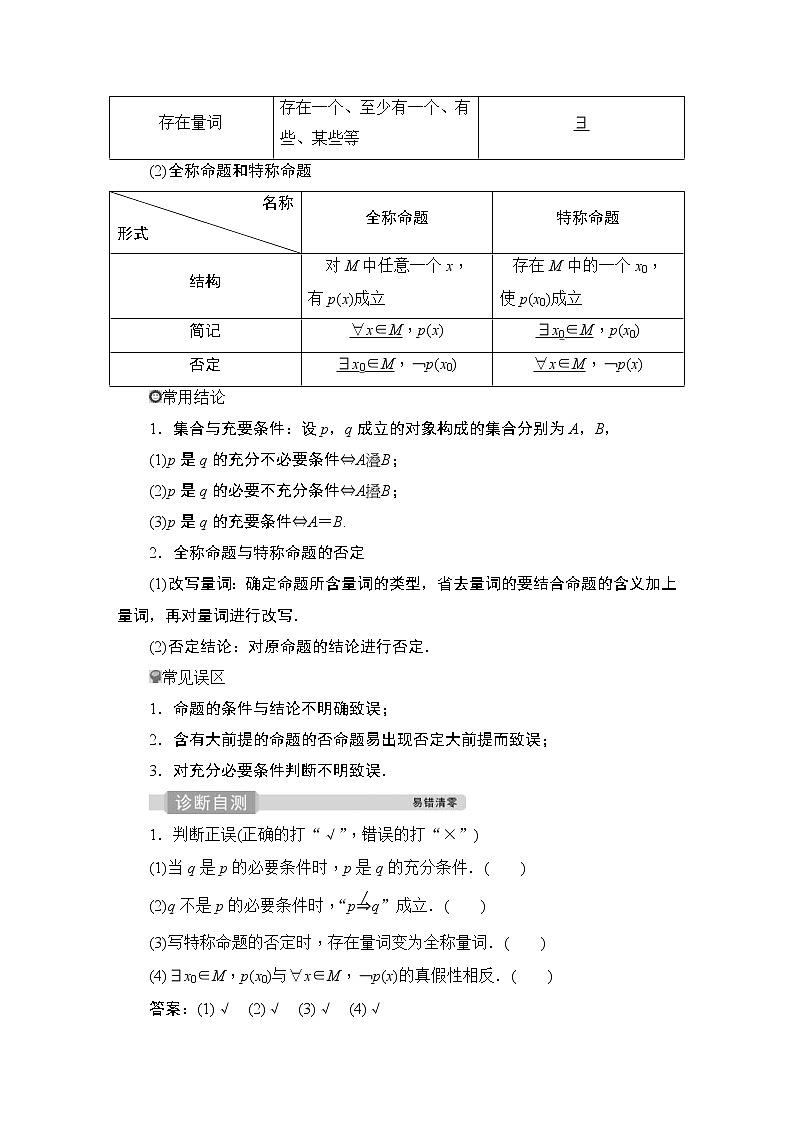
(2)全称命题和特称命题
名称
形式
全称命题
特称命题
结构
对M中任意一个x,
有p(x)成立
存在M中的一个x0,
使p(x0)成立
简记
∀x∈M,p(x)
∃x0∈M,p(x0)
否定
∃x0∈M,﹁p(x0)
∀x∈M,﹁p(x)
常用结论
1.集合与充要条件:设p,q成立的对象构成的集合分别为A,B,
(1)p是q的充分不必要条件⇔AB;
(2)p是q的必要不充分条件⇔AB;
(3)p是q的充要条件⇔A=B.
2.全称命题与特称命题的否定
(1)改写量词:确定命题所含量词的类型,省去量词的要结合命题的含义加上量词,再对量词进行改写.
(2)否定结论:对原命题的结论进行否定.
常见误区
1.命题的条件与结论不明确致误;
2.含有大前提的命题的否命题易出现否定大前提而致误;
3.对充分必要条件判断不明致误.
1.判断正误(正确的打“√”,错误的打“×”)
(1)当q是p的必要条件时,p是q的充分条件.( )
(2)q不是p的必要条件时,“pq”成立.( )
(3)写特称命题的否定时,存在量词变为全称量词.( )
(4)∃x0∈M,p(x0)与∀x∈M,﹁p(x)的真假性相反.( )
答案:(1)√ (2)√ (3)√ (4)√
2.(多选)下列命题的否定是全称命题且为真命题的有( )
A.∃x∈R,x2-x+0,所以AC均为存在性命题且为假命题,故选AC.
3.设x>0,y∈R,则“x>y”是“x>|y|”的( )
A.充要条件
B.充分不必要条件
C.必要不充分条件
D.既不充分也不必要条件
解析:选C.由x>y推不出x>|y|,由x>|y|能推出x>y,所以“x>y”是“x>|y|”的必要不充分条件.
4.(易错题)命题“全等三角形的面积一定都相等”的否定是__________________________.
答案:存在两个全等三角形的面积不相等
5.已知p:x=2,q:x-2=,则p是q的________条件.
解析:当x-2=时,两边平方可得(x-2)2=2-x,即(x-2)(x-1)=0,解得x1=2,x2=1.当x=1时,-1=,不成立,故舍去,则x=2.所以p是q的充要条件.
答案:充要
全称命题与特称命题
[题组练透]
1.下列命题中的假命题是( )
A.∀x∈R,ex>0 B.∀x∈N,x2>0
C.∃x0∈R,ln x0<1 D.∃x0∈N*,sin x0=1
解析:选B.对于B.当x=0时,x2=0,因此B中命题是假命题.
2.(2021·沈阳市教学质量监测(一))命题p:∀x∈(0,+∞),x≠x,则﹁p为( )
A.∃x0∈(0,+∞),x0=x0
B.∀x∈(0,+∞),x=x
C.∃x0∈(-∞,0),x0=x0
D.∀x∈(-∞,0),x=x
解析:选A.由全称命题的否定为特称命题知,﹁p为∃x0∈(0,+∞),x0=x0,故选A.
3.(多选)(2021·海南海口第四中学期中)下列关于二次函数y=(x-2)2-1的说法正确的是( )
A.∀x∈R,y=(x-2)2-1≥1
B.∀a>-1,∃x0∈R,y=(x0-2)2-10成立.故“a·b>0”是“a与b的夹角为锐角”的必要不充分条件.故选B.
充分条件、必要条件的探求及应用
已知条件p:集合P={x|x2-8x-20≤0},条件q:非空集合S={x|1-m≤x≤1+m}.若p是q的必要条件,求m的取值范围.
【解】 由x2-8x-20≤0,得-2≤x≤10,
所以P={x|-2≤x≤10},
由p是q的必要条件,知S⊆P.
则所以0≤m≤3.
所以当0≤m≤3时,p是q的必要条件,
即所求m的取值范围是[0,3].
【引申探究】
1.(变问法)本例条件不变,若x∈P的必要条件是x∈S,求m的取值范围.
解:由例题知P={x|-2≤x≤10},若x∈P的必要条件是x∈S,即x∈S是x∈P的必要条件,所以P⊆S,所以可以得到解得m≥9.故m的取值范围是[9,+∞).
2.(变问法)本例条件不变,是否存在实数m,使x∈P是x∈S的充要条件?
解:不存在实数m,使x∈P是x∈S的充要条件.由例题知P={x|-2≤x≤10}.若x∈P是x∈S的充要条件,则P=S,所以所以故满足题意的m不存在.
利用充要条件求参数的关注点
(1)巧用转化求参数:把充分条件、必要条件或充要条件转化为集合之间的关系,然后根据集合之间的关系列出关于参数的不等式(或不等式组)求解.
(2)端点取值慎取舍:在求参数范围时,要注意边界或区间端点值的检验,从而确定取舍.
1.命题“∀x∈[1,3],x2-a≤0”为真命题的一个充分不必要条件是( )
A.a≥9 B.a≤9
C.a≥10 D.a≤10
解析:选C.命题∀x∈[1,3],x2-a≤0⇔∀x∈[1,3],x2≤a⇔9≤a.则“a≥10”是命题“∀x∈[1,3],x2-a≤0”为真命题的一个充分不必要条件.故选C.
2.(2021·武汉质检)关于x的方程ax2+bx+c=0(a≠0)有一个正根和一个负根的充要条件是________.
解析:ax2+bx+c=0(a≠0)有一个正根和一个负根的充要条件是
即acg(x)max,即2>2+m,解得m2n,则﹁p为( )
A.∀n∈N,n2>2n B.∃x∈N,n2≤2n
C.∀n∈N,n2≤2n D.∃n∈N,n2=2n
解析:选C.因为特称命题的否定是把存在量词改为全称量词,同时否定结论,所以﹁p:∀n∈N,n2≤2n,故选C.
3.设U为全集,A,B是集合,则“存在集合C使得A⊆C,B⊆∁UC” 是“A∩B=∅”的( )
A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件
解析:选A.由A⊆C,B⊆∁UC,易知A∩B=∅,但A∩B=∅时未必有A⊆C,B⊆∁UC,如图所示,所以“存在集合C使得A⊆C,B⊆∁UC”是“A∩B=∅”的充分不必要条件.
4.已知f(x)=sin x-x,命题p:∃x∈,f(x)
相关试卷
这是一份(新高考)高考数学一轮复习素养练习 第1章 第2讲 充分条件与必要条件、全称量词与存在量词 (含解析),共10页。试卷主要包含了知识梳理,教材衍化等内容,欢迎下载使用。
这是一份2024年(新高考)高考数学一轮复习突破练习1.2《充分条件与必要条件、全称量词与存在量词》(含详解),共5页。试卷主要包含了又a>0,故a的取值范围是]等内容,欢迎下载使用。
这是一份高考数学一轮复习考点规范练2充分条件与必要条件全称量词与存在量词含解析新人教版,共7页。试卷主要包含了基础巩固,综合应用,探究创新等内容,欢迎下载使用。









