浙江省温州市3年(2020-2022)八年级数学上学期期末试题汇编3解答题
展开
这是一份浙江省温州市3年(2020-2022)八年级数学上学期期末试题汇编3解答题,共25页。试卷主要包含了解答题等内容,欢迎下载使用。
浙江省温州市3年(2020-2022)八年级数学上学期期末试题汇编03 解答题
三、解答题
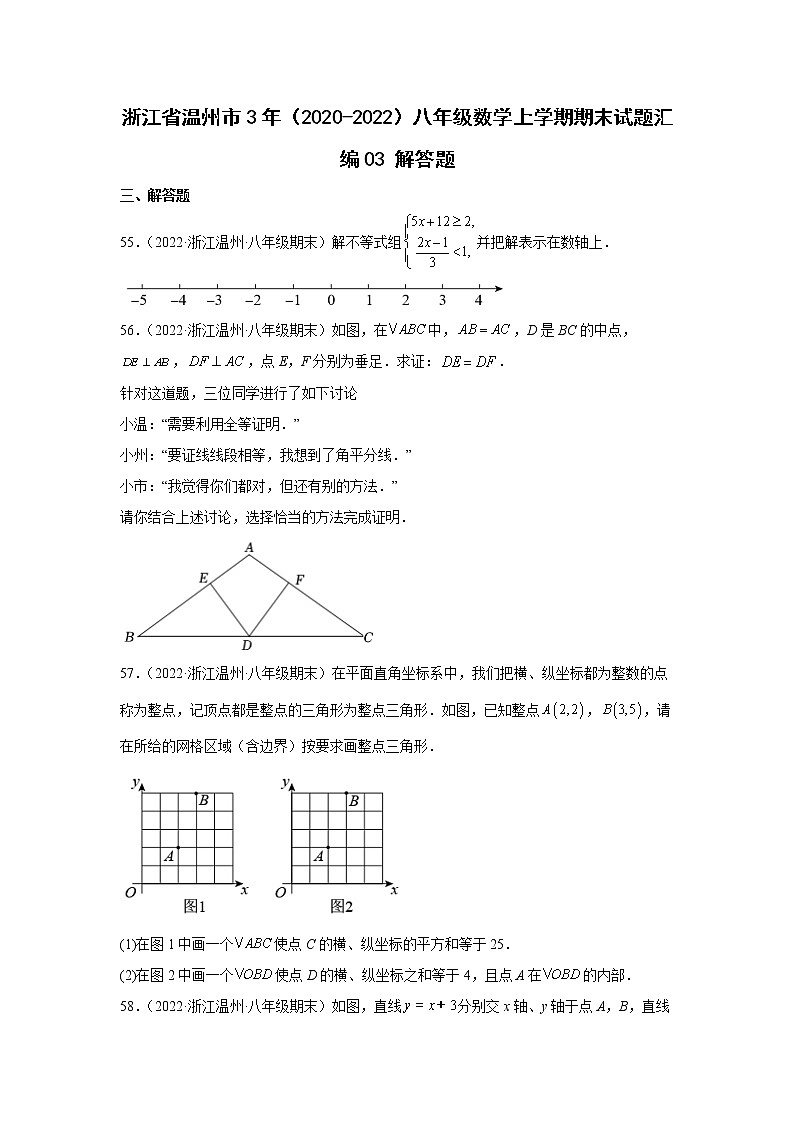
55.(2022·浙江温州·八年级期末)解不等式组并把解表示在数轴上.
56.(2022·浙江温州·八年级期末)如图,在中,,D是BC的中点,,,点E,F分别为垂足.求证:.
针对这道题,三位同学进行了如下讨论
小温:“需要利用全等证明.”
小州:“要证线线段相等,我想到了角平分线.”
小市:“我觉得你们都对,但还有别的方法.”
请你结合上述讨论,选择恰当的方法完成证明.
57.(2022·浙江温州·八年级期末)在平面直角坐标系中,我们把横、纵坐标都为整数的点称为整点,记顶点都是整点的三角形为整点三角形.如图,已知整点,,请在所给的网格区域(含边界)按要求画整点三角形.
(1)在图1中画一个使点C的横、纵坐标的平方和等于25.
(2)在图2中画一个使点D的横、纵坐标之和等于4,且点A在的内部.
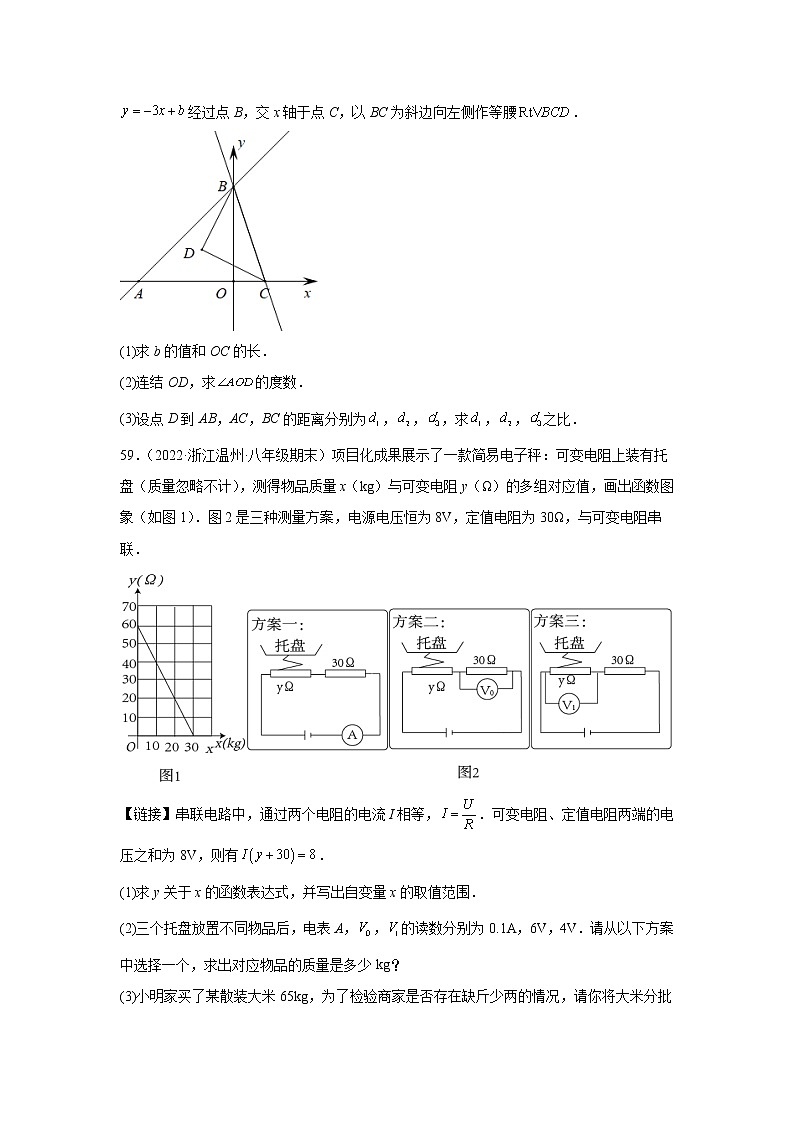
58.(2022·浙江温州·八年级期末)如图,直线分别交x轴、y轴于点A,B,直线经过点B,交x轴于点C,以BC为斜边向左侧作等腰.
(1)求b的值和OC的长.
(2)连结OD,求的度数.
(3)设点D到AB,AC,BC的距离分别为,,,求,,之比.
59.(2022·浙江温州·八年级期末)项目化成果展示了一款简易电子秤:可变电阻上装有托盘(质量忽略不计),测得物品质量x(kg)与可变电阻y(Ω)的多组对应值,画出函数图象(如图1).图2是三种测量方案,电源电压恒为8V,定值电阻为30Ω,与可变电阻串联.
【链接】串联电路中,通过两个电阻的电流I相等,.可变电阻、定值电阻两端的电压之和为8V,则有.
(1)求y关于x的函数表达式,并写出自变量x的取值范围.
(2)三个托盘放置不同物品后,电表A,,的读数分别为0.1A,6V,4V.请从以下方案中选择一个,求出对应物品的质量是多少kg?
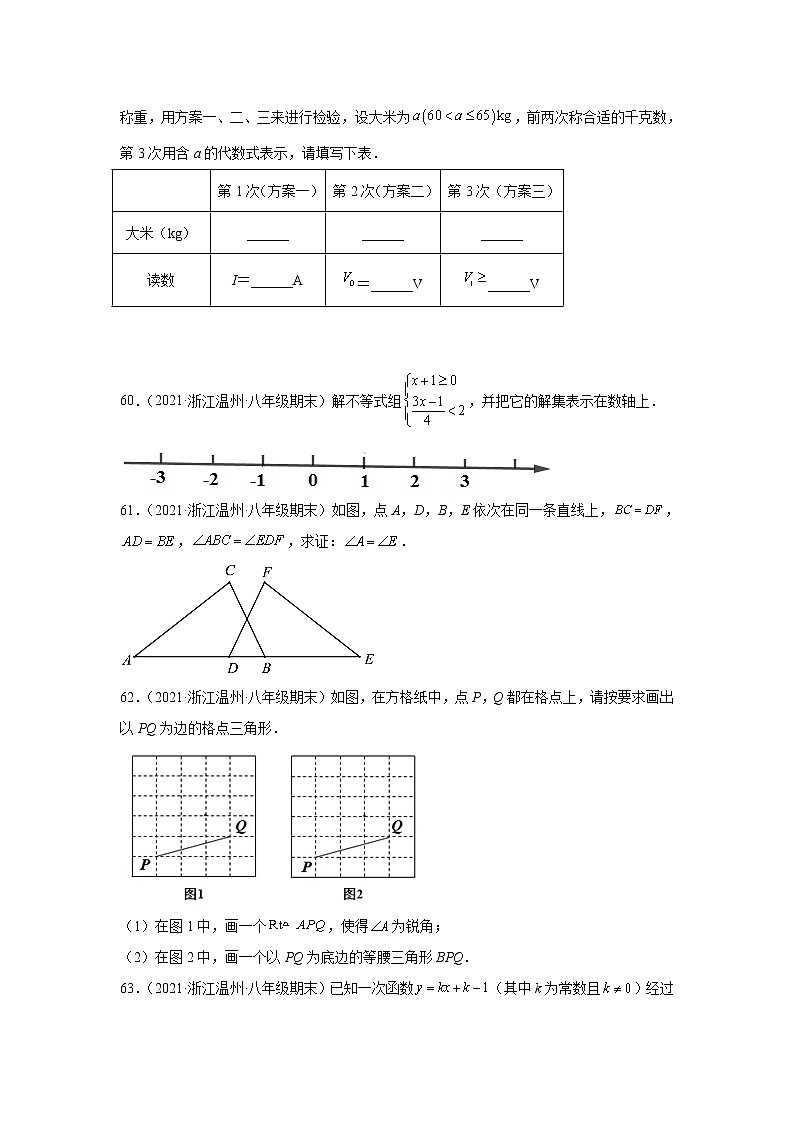
(3)小明家买了某散装大米65kg,为了检验商家是否存在缺斤少两的情况,请你将大米分批称重,用方案一、二、三来进行检验,设大米为,前两次称合适的千克数,第3次用含a的代数式表示,请填写下表.
第1次(方案一)
第2次(方案二)
第3次(方案三)
大米(kg)
______
______
______
读数
I=______A
=______V
______V
60.(2021·浙江温州·八年级期末)解不等式组,并把它的解集表示在数轴上.
61.(2021·浙江温州·八年级期末)如图,点A,D,B,E依次在同一条直线上,,,,求证:.
62.(2021·浙江温州·八年级期末)如图,在方格纸中,点P,Q都在格点上,请按要求画出以PQ为边的格点三角形.
(1)在图1中,画一个,使得为锐角;
(2)在图2中,画一个以PQ为底边的等腰三角形BPQ.
63.(2021·浙江温州·八年级期末)已知一次函数(其中k为常数且)经过点.
(1)求一次函数的表达式;
(2)当时,记函数的最大值为M,最小值为N,求的值.
64.(2021·浙江温州·八年级期末)A,B两个红十字会分别有100吨和120吨生活物资,准备直接运送给甲、乙两个灾区,甲地需160吨,乙地需60吨,A,B两地到甲、乙两地的路程以及每吨每千米的运费如图所示.
(1)设A红十字会运往甲地物资x吨,完成下表.
运量(吨)
运费(元)
A红十字会
B红十字会
A红十字会
B红十字会
甲地
乙地
(2)求总运费y关于x的函数表达式,并写出自变量x的取值范围;
(3)当A,B两红十字会各运往甲、乙两地多少吨物资时,总运费最省?最省运费是多少元?
65.(2021·浙江温州·八年级期末)如图,直线分别交x轴、y轴于点A,B,以AB为斜边向左侧作等腰,延长BD交x轴于点C,连接DO,过点D作交y轴于点E.
(1)求证:;
(2)求OE的长;
(3)点P在线段AB上,当PE与的一边平行时,求出所有符合条件的点P的坐标.
66.(2020·浙江温州·八年级期末)如图, AB=AC, AD=AE, ∠BAD=∠CAE, 求证: BE=CD.
67.(2020·浙江温州·八年级期末)解不等式组: ,并把它的解集在数轴上表示出来.
68.(2020·浙江温州·八年级期末)如图, 在方格纸中, 每一个小正方形的边长为1, 按要求画一个三角形,使它的顶点都在小方格的顶点上.
(1)在图甲中画一个以AB为边且面积为3的直角三角形
(2)在图乙中画一个等腰三角形, 使AC在三角形的内部(不包括边界)
69.(2020·浙江温州·八年级期末)如图,在等边三角形ABC中,D是AB上的一点,E是CB延长线上一点,连结CD,DE,已知∠EDB=∠ACD,
(1)求证:△DEC是等腰三角形.
(2)当∠BDC=5∠EDB, BD=2时,求EB的长.
70.(2020·浙江温州·八年级期末)某超市每天都用360元从批发商城批发甲乙两种型号“垃圾分类”垃圾桶进行零售,批发价和零售价如下表所示∶
批发价(元个)
零售价(元/个)
甲型号垃圾桶
12
16
乙型号垃圾桶
30
36
若设该超市每天批发甲型号“垃圾分类”垃圾桶x个,乙型号“垃圾分类”垃圾桶y个,
(1)求y关于x的函数表达式.
(2)若某天该超市老板想将两种型号的“垃圾分类”垃圾桶全部售完后,所获利润率不低于30%,则该超市至少批发甲型号“垃圾分类”垃圾桶多少个?(利润率=利润/成本).
71.(2020·浙江温州·八年级期末)如图,在平面直角坐标系中,已知点A的坐标为(15,0),点B的坐标为(6,12),点C的坐标为(0,6), 直线AB交y轴于点D, 动点P从点C出发沿着y轴正方向以每秒2个单位的速度运动, 同时,动点Q从点A出发沿着射线AB以每秒a个单位的速度运动设运动时间为t秒,
(1)求直线AB的解析式和CD的长.
(2)当△PQD与△BDC全等时,求a的值.
(3)记点P关于直线BC的对称点为,连结当t=3,时, 求点Q的坐标.
【答案】
55.,数轴见解析.
【分析】分别解得两个不等式的解集,并将解集表示在数轴上,找到公共解集即可解题.
【详解】解:解不等式,得,
解不等式,得,
原不等式组的解是,
把两个不等式的解表示在数轴上,如图,
【点睛】本题考查解不等式组,在数轴上表示不等式组的解集,是重要考点,掌握相关知识是解题关键.
56.见解析
【分析】小温的方法:由AB=AC得∠B=∠C,由DE⊥AB,DF⊥AC,点E,F分别为垂足得∠BED=∠CFD=90°,又因为BD=CD,所以可以通过证明△BED≌△CFD证明DE=DF;
小州的方法:连结AD,根据等腰三角形的“三线合一”性质证明AD平分∠BAC,再根据解平分线的性质证明DE=DF;
小市的方法:连结AD,根据S△ABD=S△ACD列等式AB•DE=AC•DF,证明DE=DF.
【详解】证明:小温的证明方法:∵AB=AC,
∴∠B=∠C,
∵DE⊥AB,DF⊥AC,点E,F分别为垂足,
∴∠BED=∠CFD=90°,
∵D是BC的中点,
∴BD=CD,
在△BED和△CFD中,
,
∴△BED≌△CFD(AAS),
∴DE=DF.
小州的证明方法:如图,连结AD,
∵AB=AC,D是BC的中点,
∴∠BAD=∠CAD,
∵DE⊥AB,DF⊥AC,点E,F分别为垂足,
∴DE=DF.
小市的证明方法:如图,连结AD,
∵AB=AC,D是BC的中点,
∴AD⊥BC,
∵BD=CD=BC,
∴S△ABD=S△ACD,
∵DE⊥AB,DF⊥AC,点E,F分别为垂足,
∴S△ABD=AB•DE,S△ACD=AC•DF,
∴AB•DE=AC•DF,
∴DE=DF.
【点睛】此题考查等腰三角形的性质、全等三角形的判定与性质、角平分线的性质、利用面积等式解题等知识与方法,此题综合性较强,解题方法较多.
57.(1)见解析
(2)见解析
【分析】(1)根据题意画图即可;
(2)根据题意画图即可;
(1)
解:(1)画法不唯一,如下图.
(2)
画法不唯一,如下图.
【点睛】本题考查网格作图、平面直角坐标系等知识,是基础考点,掌握相关知识是解题关键.
58.(1),
(2)45°
(3)
【分析】(1)首先求出A、B两点坐标,将点B的坐标代入直线y=-3x+b,即可求解;
(2)连接OD,作DE⊥OD交y轴于E,证明△DBE≌△DCO,根据全等三角形的性质得DE=DO,∠DOE=45°,即可得∠AOD=45°;
(3)延长OD交AB于H,过D作DM⊥AC于M,DN⊥BC于N,DF⊥OB于F,则d2=DM,d3=DN,证明DH⊥AB,得d1=DH,分别求出DM,DN,DH,即可求解.
(1)
解:直线y=x+3分别交x轴、y轴于点A,B,
当x=0时,y=3;当y=0时,x=-3;
∴点A(-3,0)、B(0,3),
∵直线y=-3x+b经过点B(0,3),
将点B的坐标(0,3)代入直线y=-3x+b得:b=3,
∴y=-3x+3
当y=0时,-3x+3=0,解得x=1,
∴C(1,0),
∴OC=1;
(2)
连接OD,作DE⊥OD交y轴于E,
∵Rt△BCD是等腰直角三角形,
∴∠BDC=90°,DB=DC,
∴∠BDE+∠EDC=90°,
∵DE⊥OD,
∴∠CDO+∠EDC=90°,
∴∠BDE=∠CDO,
设CD、OB交于Q,
∵∠BDC=∠QOC=90°,∠BQD=∠CQO,
∴∠DBE=∠DCO,
∵DB=DC,∠BDE=∠CDO,
∴△DBE≌△DCO(ASA),
∴DE=DO,
∵DE⊥OD,
∴∠DOE=45°,
∴∠AOD=45°;
(3)
延长OD交AB于H,过D作DM⊥AC于M,DN⊥BC于N,DF⊥OB于F,则d2=DM,d3=DN,
∵△DBE≌△DCO,C(1,0),
∴BE=CO=1,
∵A(-3,0)、B(0,3),
∴OE=2,OA=OB=3,
∵DE=DO,DE⊥OD,
∴
延长OD交AB于点Q,
∵OD平分,,
∴.
在等腰中,,
,
∴.
【点睛】本题主要考查了一次函数的应用、等腰直角三角形的性质、全等三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题.
59.(1),自变量x的取值范围是
(2)方案一:5kg;方案二:25kg;方案三:15kg;
(3)20,20,a-40,0.16,4,2
【分析】(1)利用待定系数法解题;
(2)选择方案一:由解答;选择方案二:由题意得,由此解得,再把代入一次函数解析式中;选择方案三:由题意得电阻之比等于电压之比解题;
(3)由公式解题.
(1)
解:(1)根据图象得:y是x的一次函数,设,
将,代入,得,解得
∴所求函数表达式为
自变量x的取值范围是.
(2)
(2)选择方案一:由题意得,则,
将代入,得,即物品的质量是5kg;
选择方案二:由题意得,则,
将代入,得,即物品的质量是25 kg;
选择方案三:由题意得电阻之比等于电压之比,即,∴,
将代入,得,即物品的质量是15 kg.
(3)
填表方案不唯一,如:
方案一:取大米20kg,将代入中,得,
方案二:取大米20kg, 将代入中,得,
方案二:取大米kg, 将代入中,得
由题意得电阻之比等于电压之比,即,
解得
第1次(方案一)
第2次(方案二)
第3次(方案三)
大米(kg)
20
20
a-40
读数
I= 0.16 A
= 4 V
2 V
【点睛】本题以物理中的电路问题为背景,考查求解一次函数关系式,难度一般,掌握相关知识是解题关键.
60.,在数轴上表示见解析.
【分析】先对不等式组进行化简,然后在数轴上分别画出x的取值,它们的公共部分就是不等式组的解集.
【详解】解:
由①得:
由②得:,
∴,
∴不等式组的解集为
在数轴上表示如下:
【点睛】本题考查了一元一次不等式组的解,解此类题目常常要结合数轴来判断.要注意x是否取得到,若取得到则x在该点是实心的.反之x在该点是空心的.
61.证明见解析.
【分析】先根据已知条件得出,再利用SAS证明,最后根据全等三角形的性质即可得出答案.
【详解】证明:∵,
∴,
∴.
在和中,
,
∴,
∴.
【点睛】本题考查了全等三角形的判定及性质,熟练掌握全等三角形的判定方法是解题的关键.
62.(1)答案见解析;(2)答案见解析
【分析】(1)利用等腰直角三角形的定义、数形结合的思想解决问题即可;
(2)根据等腰三角形的定义画出图形即可.
【详解】(1)△APQ即为所求(答案不唯一).
(2)△BPQ即为所求(答案不唯一).
【点睛】本题考查了作图-应用与设计,等腰直角三角形等知识,解题的关键是学会利用数形结合的思想解决问题,属于中考常考题型.
63.(1);(2)6.
【分析】(1)将点(2,5)代入,即可求解;
(2)先判断出函数y随x的增大而增大,求得当时,y有最小值,当时,y有最大值,计算即可求解.
【详解】(1)∵一次函数经过点(2,5),
∴,
∴k=2,
∴一次函数的表达式为;
(2)∵中,,
∴y随x的增大而增大,
∵,
∴当时,y有最小值N,即:,
当时,y有最大值M,即:,
∴.
【点睛】本题考查了待定系数法求一次函数的解析式,一次函数的性质,关键是熟练掌握一次函数的性质,灵活运用性质解题.
64.(1),,,;(2),自变量x的取值范围是:;(3)当A运往甲、乙分别为40吨、60吨,B运往甲、乙分别为120吨、0吨时费用最省,为7260元.
【分析】(1)根据题意及图中的信息可直接得出答案;
(2)根据4个运费相加再化简即可得出答案;
(3)根据一次函数的性质即可得出最大值,从而得出方案.
【详解】解:(1)
运量(吨)
运费(元)
A红十
字会
B红十
字会
A红十
字会
B红十
字会
甲地
乙地
(2)总运费
自变量x的取值范围是:.
(3)∵中,,
∴y随x的增大而增大.
∵,
∴当时,元
此时A运往甲、乙分别为40吨、60吨,B运往甲、乙分别为120吨、0吨.
【点睛】本题考查了一次函数的应用,熟练掌握一次函数的性质是解题的关键.
65.(1)证明见解析;(2)8;(3)点P的坐标为或.
【分析】(1)根据同角的余角相等得出;
(2)先证,得出,再根据得出结论;
(3)分两种情况讨论①,②.
【详解】解:(1)如图,∵,
∴,,
∴.
(2)如图,∵,,
∴,,
∴.
∵,且,
∴,
∴.
又∵直线分别交x轴、y轴于点A,B,
∴,,
∴,
∴.
(3)∵直线PE与的一边平行,
∴分两种情况.
①若(如图)
则,
又∵点P在直线上
令,则,∴P为
②若(如图),延长EP交x轴于点Q,
由(2)知:,∴.
∵,∴,
∴,∴为.
设直线EP为:,
则,∴,∴.
联立,得,∴,∴P为,
综上所述:符合条件的点P的坐标为或.
【点睛】本题考查了一次函数的性质及全等三角形的判定与性质,解题的关键是掌握分类讨论思想的运用.
66.证明见解析
【分析】先根据角的和差求出,再根据三角形全等的判定定理与性质即可得证.
【详解】
,即
在与中,
.
【点睛】本题考查了三角形全等的判定定理与性质,熟记判定定理与性质是解题关键.
67.,数轴图见解析.
【分析】先分别求出不等式①和②的解,再找出两个解的公共部分即可得出不等式组的解集,然后根据数轴的定义将其表示出来即可.
【详解】不等式①,移项合并得:
不等式②,去括号得:
移项合并得:
故原不等式组的解集是,将其在数轴上表示出来如下:
【点睛】本题考查了一元一次不等式组的解法、数轴的定义,掌握不等式组的解法是解题关键.
68.(1)答案见解析;(2)答案见解析.
【分析】(1)根据直角三角形的面积公式可知,AB只能是一条直角边,从而可知另一条直角边的边长为3,由此即可画出图形;
(2)在正方形网格中,先利用勾股定理画出相等的两条边,再连接即可得出符合条件的等腰三角形.
【详解】(1)以AB为边且面积为3的直角三角形作图结果如下:(二选一)
(2)使AC在三角形的内部的等腰三角形的作图结果如下:(三选一)
【点睛】本题考查了直角三角形的定义、等腰三角形的定义、勾股定理,掌握定义是解题关键.
69.(1)证明见解析;(2).
【分析】(1)先根据等边三角形的性质可得,再根据角的和差、外角的性质可得,然后根据等腰三角形的判定定理即可得证;
(2)先根据角的和差倍分求出的度数,从而可得是等腰直角三角形,再利用直角三角形的性质、等边三角形的性质求出的长,然后由线段的和差即可得.
【详解】(1)是等边三角形
是等腰三角形;
(2)如图,过点D作于点F
是等腰直角三角形
故EB的长为.
【点睛】本题考查了等边三角形的性质、等腰三角形的判定定理、直角三角形的性质等知识点,较难的是题(2),通过作辅助线,构造一个等腰直角三角形是解题关键.
70.(1);(2)23.
【分析】(1)根据甲、乙两型号垃圾桶的批发价和个数、总花费列出等式,再进行等式变形即可得;
(2)先根据表格中的数据求出利润的表达式,再根据“利润率利润/成本”得出一个不等式,然后结合题(1)求解即可.
【详解】(1)由题意得:
整理得:
故y关于x的函数表达式为;
(2)由甲、乙型号垃圾桶的价格表得:全部售完后的利润为
由题意得:
将(1)的结论代入得:
解得:
都是正整数
∴ x最小为23
答:该超市至少批发甲型号垃圾桶23个,所获利润率不低于.
【点睛】本题考查了一次函数的实际应用,一元一次不等式的实际应用,依据题意正确列出不等式是解题关键.
71.(1),14;(2)a的值为5.5或3.25或2.5;(3).
【分析】(1)先利用待定系数法求出直线AB的解析式,再令求出点D的坐标,从而可得出CD的长;
(2)先利用点坐标求出BD、AD的长,分点P在CD上和点P在CD延长线上,再利用三角形全等的性质求出DP、DQ的长,最后利用线段的和差即可得;
(3)如图4(见解析),连结BP,过点Q作,交延长线于点E,先求出CP的长,再根据点B的坐标可推出,然后可求出BP的长,从而可求出,根据点的对称性可得,又根据平行线的性质可得,最后根据等腰三角形的性质、一次函数的性质即可求出答案.
【详解】(1)设直线AB的解析式为
把点代入得
解得
故直线AB的解析式为
令,代入得
则点D的坐标为
故;
(2)
①如图1,当点P在CD上时,点P只能与点B是对应点
则
解得;
②如图2,当点P在CD延长线上,并且点P与点B是对应点时
则
解得;
③如图3,当点P在CD延长线上,并且点P与点C是对应点时
则
解得;
综上,a的值为5.5或3.25或2.5;
(3)如图4,连结BP,过点Q作,交延长线于点E
,与点B的纵坐标相等
,即
∵点P与点关于直线BC对称
是等腰直角三角形,且
设,则点Q的坐标为,即
将代入得,
解得
故点Q的坐标为.
【点睛】本题考查了利用待定系数法求函数的解析式、三角形全等的性质、点的对称性、等腰三角形的性质等知识点,较难的是题(3),通过作辅助线,推出是解题关键.
相关试卷
这是一份浙江省杭州市上城区3年(2020-2022)八年级数学上学期期末试题汇编3解答题,共29页。试卷主要包含了解答题等内容,欢迎下载使用。
这是一份浙江省杭州市拱墅区3年(2020-2022)八年级数学上学期期末试题汇编3解答题,共26页。试卷主要包含了解答题,四象限,不经过第一象限.等内容,欢迎下载使用。
这是一份浙江省宁波市奉化区3年(2020-2022)八年级数学上学期期末试题汇编3解答题,共27页。试卷主要包含了解答题等内容,欢迎下载使用。









