浙江省金华市婺城区3年（2020-2022）八年级数学上学期期末试题汇编2填空题

浙江省金华市婺城区3年（2020-2022）八年级数学上学期期末试题汇编02 填空题

二、填空题

31．（2021·浙江金华·八年级期末）武汉市某一天的最低气温为-6℃，最高气温是5℃，如果设这天气温为t℃，那么t应满足条件______ ．

32．（2021·浙江金华·八年级期末）如图，点B、F、C、E在一条直线上，ABED， AB=DE，要使△ABC≌△DEF，可以添加的一个条件是：________．

33．（2021·浙江金华·八年级期末）小丽同学准备用自己节省的零花钱购买一台学生平板电脑，她已存有750元，并计划从本月起每月节省30元，直到她至少存有1080元．设x个月后小丽至少有1080元，则根据题意可列不等式为______________________．

34．（2021·浙江金华·八年级期末）如图，在△ABC中，AB=AC，AD是BC边上的高，点E、F是AD的三等分点，若△ABC的面积为12cm2，则图中阴影部分的面积是________cm2．

35．（2021·浙江金华·八年级期末）点P是平面直角坐标系中的一点且不在坐标轴上，过点P向x轴，y轴作垂线段，若垂线段的长度的和为4，则点P叫做“垂距点”，例如：如图中的P（1，3）是“垂距点”． 若D（，）为“垂距点”，则m=________．

36．（2021·浙江金华·八年级期末）在每个小正方形的边长为1的网格图形中，每个小正方形的顶点称为格点．以顶点都是格点的正方形ABCD的边为斜边，向内作四个全等的直角三角形，使四个直角顶点E，F，G，H都是格点，且四边形EFGH为正方形，我们把这样的图形称为格点弦图．例如，在如图1所示的格点弦图中，正方形ABCD的边长为，此时正方形EFGH的而积为5．问：当格点弦图中的正方形ABCD的边长为时，正方形EFGH的面积的所有可能值是_____（不包括5）．

37．（2022·浙江金华·八年级期末）写出一个过点（0，3），且y随x的增大而减小的一次函数解析式__________．

38．（2022·浙江金华·八年级期末）甲种蔬菜保鲜的适宜温度（单位：℃）是，乙种蔬菜保鲜的适宜温度是，将这两种蔬菜放在一起同时保鲜，则保鲜的适宜温度t（单位：℃）的范围是______．

39．（2022·浙江金华·八年级期末）将如图所示的“QQ”笑脸放置在3×3的正方形网格中，A、B、C三点均在格点上．若A、B的坐标分别为（－2，1），（－3，2），则点C的坐标为______．

40．（2022·浙江金华·八年级期末）如图，在Rt△ABC中，∠B=90°，以顶点C为圆心、适当长为半径画弧，分别交AC、BC于点E、F，再分别以点E、F为圆心，以大于EF的长为半径画弧，两弧交于点P，作射线CP交AB于点D．若BD=4，AC=16，则△ACD的面积是______．

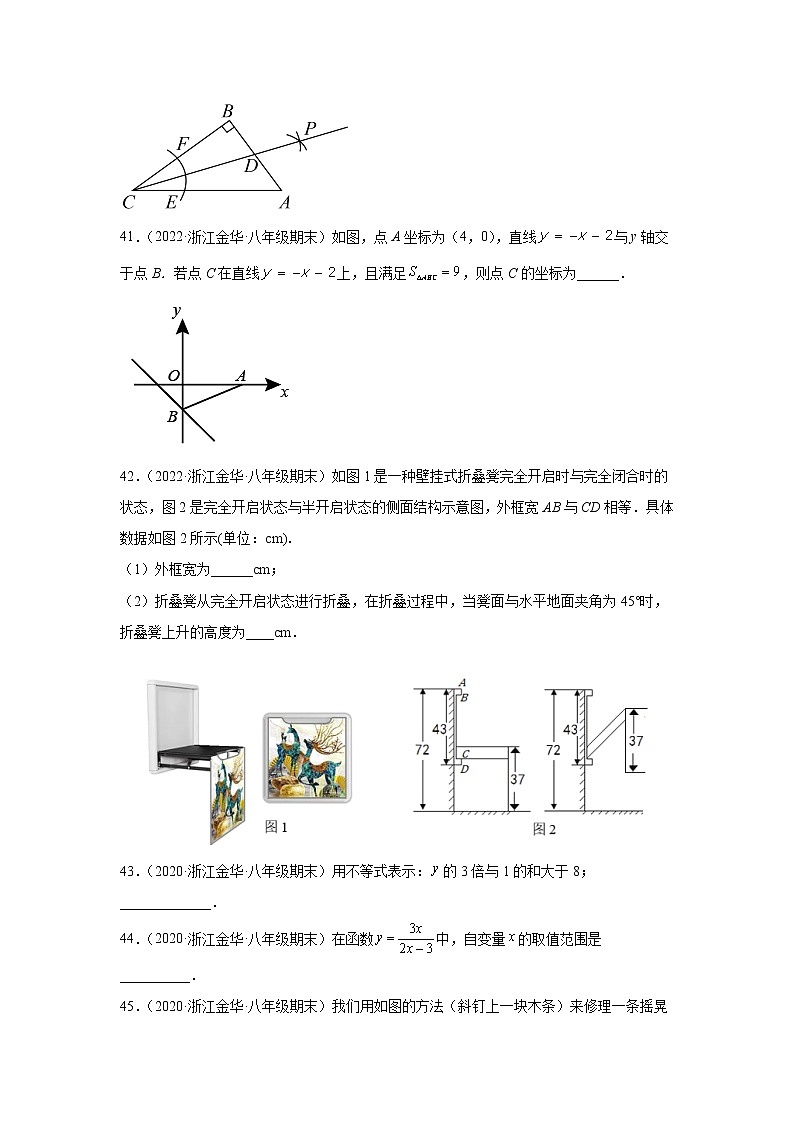
41．（2022·浙江金华·八年级期末）如图，点A坐标为（4，0），直线与y轴交于点B．若点C在直线上，且满足，则点C的坐标为______．

42．（2022·浙江金华·八年级期末）如图1是一种壁挂式折叠凳完全开启时与完全闭合时的状态，图2是完全开启状态与半开启状态的侧面结构示意图，外框宽AB与CD相等．具体数据如图2所示(单位：cm)．

（1）外框宽为______cm；

（2）折叠凳从完全开启状态进行折叠，在折叠过程中，当凳面与水平地面夹角为45°时，折叠凳上升的高度为____cm．

43．（2020·浙江金华·八年级期末）用不等式表示：的3倍与1的和大于8；_____________．

44．（2020·浙江金华·八年级期末）在函数中，自变量的取值范围是__________．

45．（2020·浙江金华·八年级期末）我们用如图的方法（斜钉上一块木条）来修理一条摇晃的凳子的数学原理是利用三角形的___．

46．（2020·浙江金华·八年级期末）如图，正方形纸片的边长为12，是边上一点，连接．折叠该纸片，使点落在上的点，并使折痕经过点，得到折痕，点在上．若，则的长为__________．

47．（2020·浙江金华·八年级期末）如图，把平面内一条数轴绕原点逆时针旋转角得到另一条数轴，轴和轴构成一个平面斜坐标系．规定：过点作轴的平行线，交轴于点，过点作轴的平行线，交轴于点，若点在轴上对应的实数为，点在轴上对应的实数为，则称有序实数对为点的斜坐标，在某平面斜坐标系中，已知，点的斜坐标为，点与点关于轴对称，则点的斜坐标为___________．

48．（2020·浙江金华·八年级期末）在直角坐标系中，已知、，，在的边上取两点、（点是不同于点的点），若以、、为顶点的三角形与全等，则符合条件的点的坐标为__________．

【答案】

31．-6℃≤t≤5℃

【分析】由于题目出现了最高气温与最低气温，只需要t大于等于最低气温，小于等于最高气温即可；接下来只需要根据具体的数值即可列出不等式，即写出t的取值范围.

【详解】由最低气温为-6℃，最高气温是5℃，可得-6≤t≤5.

故答案为-6℃≤t≤5℃.

【点睛】本题考查了列不等式表示数量关系，根据题意找出不等量关系式解答本题的关键．

32．∠A=∠D(答案不唯一）

【分析】根据平行线的性质可得∠B=∠E，又因为AB=DE，然后再利用全等三角形的判定方法即可解答．

【详解】解：∵ABED，

∴∠B=∠E，

∵AB=DE，

可添加的一个条件∠A=∠D，

∴△ABC≌△DEF（ASA），

故答案为：∠A=∠D(答案不唯一)．

【点睛】本题考查了全等三角形的判定，熟练掌握全等三角形的判定定理是解题的关键．

33．30x＋750≥1080

【分析】本题的不等关系为：已存的钱与每月节省的钱数之和至少为1080元．至少即大于等于．

【详解】解：根据题意，得

．

故答案为.

【点睛】考查了由实际问题抽象出一元一次不等式，抓住关键词语，弄清不等关系，才能把文字语言的不等关系转化为用数学符号表示的不等式．

34．6

【分析】根据等腰三角形是轴对称图形知，△CEF和△BEF的面积相等，所以阴影部分的面积是三角形面积的一半．

【详解】解：∵△ABC中，AB=AC，AD是BC边上的高，

∴△ABC是轴对称图形，且直线AD是对称轴，

∴△CEF和△BEF的面积相等，

∴S阴影=S△ABD，

∵AB=AC，AD是BC边上的高，

∴BD=CD，

∴S△ABD=S△ACD=S△ABC，

∵S△ABC=12cm2，

∴S阴影=12÷2=6(cm2)．

故答案为：6．

【点睛】本题考查了等腰三角形的性质及轴对称性质；利用对称发现并利用△CEF和△BEF的面积相等是正确解答本题的关键．

35．±2

【分析】根据“垂距点”的定义，得到+=4，求解即可；

【详解】解：根据题意得|+=4，

①当m>0时，

则2m=4，解得m=2，

②当m<0时，则-2m=4，

解得m=-2，

故m的值为±2．

故答案为：±2．

【点睛】本题考查新定义，解绝对值方程，根据新定义正确列出方程是解题的关键．

36．9或13或49.

【详解】分析：共有三种情况：①当DG=，CG=2时，满足DG2+CG2=CD2，此时HG=，可得正方形EFGH的面积为13；

②当DG=8，CG=1时，满足DG2+CG2=CD2，此时HG=7，可得正方形EFGH的面积为49；

③当DG=7，CG=4时，满足DG2+CG2=CD2，此时HG=3，可得正方形EFGH的面积为9.

详解：①当DG=，CG=2时，满足DG2+CG2=CD2，此时HG=，可得正方形EFGH的面积为13．

②当DG=8，CG=1时，满足DG2+CG2=CD2，此时HG=7，可得正方形EFGH的面积为49；

③当DG=7，CG=4时，满足DG2+CG2=CD2，此时HG=3，可得正方形EFGH的面积为9.

故答案为9或13或49．

点睛：本题考查作图-应用与设计、勾股定理等知识，解题的关键是学会利用数形结合的思想解决问题，属于中考填空题中的压轴题．

37．y=-x+3（答案不唯一）

【分析】设函数y=kx+b (k≠0,k,b为常数)，由图象经过点(0,3)则b=3，又y随x的增大而减小，只要k<0即可．

【详解】解：设函数y=kx+b (k≠0,k,b为常数)，

∵图象经过点(0,3) ．

∴b=3，

又∵y随x的增大而减小，

∴k<0，可取k=−1．

这样满足条件的函数可以为： y=−x+3．

故答案为：y=−x+3．

【点睛】本题考查了一次函数y=kx+b (k≠0,k,b为常数)的性质．它的图象为一条直线，当k>0，图象经过第一，三象限，y随x的增大而增大； k<0，图象经过第二，四象限，y随x的增大而减小；当b>0，图象与y轴的交点在x轴的上方；当b=0，图象过坐标原点；当b<0，图象与y轴的交点在x轴的下方．

38．

【分析】找出两种蔬菜温度的公共部分即可．

【详解】解：因为甲种蔬菜保鲜的适宜温度是，乙种蔬菜保鲜的适宜温度是，

所以将这两种蔬菜放在一起同时保鲜，保鲜的适宜温度范围是．

故答案为：．

【点睛】本题考查了一元一次不等式组的应用，正确理解题意、掌握解答的方法是关键．

39．（﹣2，2）

【分析】先根据A、B的坐标建立平面直角坐标系，再结合平面直角坐标系可得点C坐标．

【详解】解：先根据A、B的坐标建立平面直角坐标系，如图所示，

由图可得点C的坐标为（﹣2，2），

故答案为：（﹣2，2）．

【点睛】本题主要考查坐标确定位置，解题的关键是根据已知点的坐标建立平面直角坐标系．

40．32

【分析】过点D作DQ⊥AC，由作法可知CP是角平分线，根据角平分线的性质知DB=DQ=3，再由三角形的面积公式计算即可．

【详解】解：如图，过点D作DQ⊥AC于点Q，

由作图知CP是∠ACB的平分线，

∵∠B=90°，BD=4，

∴DB=DQ=4，

∵AC=16，

∴S△ACD=•AC•DQ=，

故答案为32．

【点睛】本题主要考查作图-基本作图，三角形面积，解题的关键是掌握角平分线的尺规作图及角平分线的性质．

41．(3，-5)或（-3，1）

【分析】设C点坐标为（c，-c-2），利用三角形面积公式列方程求出c，从而得到C点坐标．

【详解】解：如图，设C点坐标为（c，-c-2），直线与x轴交于点D，

∵直线与y轴交于点B，与x轴交于点D，

∴B（0，-2），D（-2，0），

∵点A坐标为（4，0），

∴AD=4-（-2）=6，

∴S△ABC＝=9，

∴＝3，

解得：c＝3或c＝﹣3，

∴点C的坐标为（3，-5）或（﹣3，1）．

故答案为：(3，-5)或（-3，1）．

【点睛】此题考查了一次函数有关的面积问题，解题的关键是熟练掌握一次函数图象与性质．

42．     3     ．

【分析】（1）如图3，由折叠的性质知，BC=，再由线段的和差关系求解．

（2）如图4，当凳面与水平地面夹角为45°时，过点E作EH⊥，那么凳面上升的高度即为的长度．再根据折叠的性质，由线段的和差关系求解．

【详解】（1）解：如图3，设壁挂式折叠凳完全开启时上凳面为，下凳面为，上凳面到地面的距离为=37cm，完全闭合时的状态折叠凳到地面的距离为AF=72cm，

由折叠的性质知，

BC==37cm，

∵AD=43cm，AB=CD，

∴外框宽AB=CD=(43-37)÷2=3cm，

故答案为：3．

（2）解：如图4，当凳面与水平地面夹角为45°时，过点E作EH⊥，那么凳面上升的高度即为的长度．

∵由图3知，，

，

∴EC=37-32=5cm，

∴由折叠的性质知=，

∵∠=45°， EH⊥，

∴是等腰直角三角形．

∴，，

即2，

又∵=32cm，

∴=16cm．

故答案为：16．

【点睛】此题考查了求线段的长度、勾股定理、折叠的性质，解题的关键是读懂题意，构造直角三角形，由勾股定理求解．

43．.

【分析】关系式为：y的3倍，把相关数值代入即可.

【详解】解：根据题意，可列不等式：，

故答案为：.

【点睛】考查列一元一次不等式，根据关键词得到相应的关系式是解决本题的关键.

44．

【分析】根据分式的分母不为零即可确定自变量的取值范围.

【详解】解：函数中分母，

∴；

故答案为；

【点睛】本题主要考查了函数及分式的概念，明确分式的分母不为零这一条件是解题的关键.

45．稳定性．

【分析】当三角形三边的长度确定后，三角形的形状和大小就能唯一确定下来，故三角形具有稳定性，根据三角形具有稳定性回答即可．

【详解】用如图的方法（斜钉上一块木条）来修理一条摇晃的凳子的数学原理是利用三角形的稳定性，故答案为稳定性．

【点睛】本题考查了三角形的稳定性，解题的关键是了解三角形具有稳定性，四边形不具有稳定性．

46．

【分析】先根据勾股定理得出AE的长，然后根据折叠的性质可得BF垂直平分AG，再根据,求出AM 的长，从而得出AG,继而得出GE的长

【详解】解：在正方形中，∠BAD=∠D =，

∴∠BAM+∠FAM=

在Rt中，

∵由折叠的性质可得

∴AB=BG，∠FBA=∠FBG

∴BF垂直平分AG，

∴AM=MG，∠AMB=

∴∠BAM+∠ABM=

∴∠ABM=∠FAM

∴

∴ ，∴

∴AM=,   ∴AG=

∴GE=13-

【点睛】本题考查了正方形与折叠，勾股定理，等腰三角形的性质，以及三角形相似的判定和性质，熟练掌握相关的知识是解题的关键

47．

【分析】如图作轴交轴于，作轴交轴于.交轴于.利用全等三角形的性质，平行四边形的性质求出、即可.

【详解】解：如图作轴交轴于，作轴交轴于.交轴于.

，，，

，

，，

在中，，，

，

，

，

，

故答案为

【点睛】本题考查坐标与图形变化，轴对称等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，属于中考常考题型.

48．，，，

【分析】先求出AC直线解析式，再根据题意分情况作图，根据坐标特点即可求解.

【详解】∵，

∴CO=,AO=6，AC=4

∴∠CAO=30°，

设直线AC为y=kx+b

把A,C代入直线得

解得

∴直线AC为：y=x+

如图1，当OP平分∠CPF时，△OFP≌△OQP，

∵，∴P点横坐标为3，

故P

如图2，当AO=AP,OF=PQ时，△OFP≌△PQO，

作PG⊥AO，∵AP=AO=6，∠CAO=30°，

∴PG=AP=3，

∴P点纵坐标为3，代入直线AC得P，

如图3，当P,Q分别是CO,AC中点时，PQ=OF,PO=QF，△OFP≌△PQO，

∴OP=CO=

∴P，

如图4，当P点在第一象限角平分线时，QP=FP,OF=OQ，△OFP≌△OQP

把x=y代入直线AC得，x=y=

∴P

综上：P点坐标为，，，

故答案为：，，，.

【点睛】此题主要考查坐标与图形，解题的关键是熟知全等三角形的判定、一次函数的图像与性质.