(新高考)高考数学一轮复习课件第2章§2.10《函数模型的应用》(含解析)

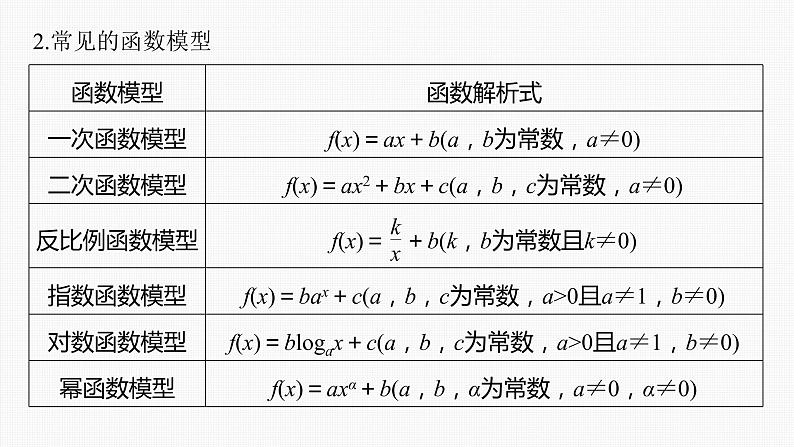
这是一份(新高考)高考数学一轮复习课件第2章§2.10《函数模型的应用》(含解析)，共60页。PPT课件主要包含了落实主干知识，常见的函数模型，探究核心题型，由题意得，只要写，课时精练，训练后立定跳远距离为，解得t＝6，显然A正确B错误，当x＝12时等内容，欢迎下载使用。
1.了解指数函数、对数函数与一次函数增长速度的差异.2.理解“指数爆炸”“对数增长”“直线上升”等术语的含义.3.会选择合适的函数模型刻画现实问题的变化规律，了解函数模型在社会生活中的广 泛应用.
LUOSHIZHUGANZHISHI
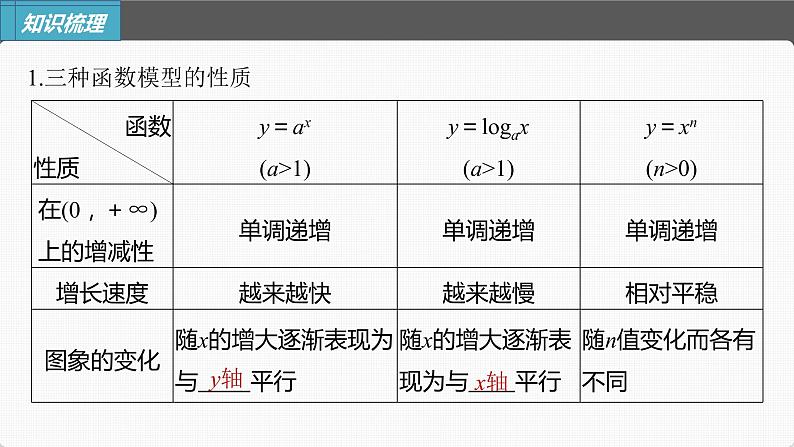
1.三种函数模型的性质
判断下列结论是否正确(请在括号中打“√”或“×”)(1)函数y＝2x的函数值比y＝x2的函数值大．(　　)(2)某商品进价为每件100元，按进价增加10%出售，后因库存积压降价，若九折出售，则每件还能获利．(　　)(3)在(0，＋∞)上，随着x的增大，y＝ax(a>1)的增长速度会超过并远远大于y＝xa(a>0)和y＝lgax(a>1)的增长速度．(　　)(4)在选择实际问题的函数模型时，必须使所有的数据完全符合该函数模型．(　　)
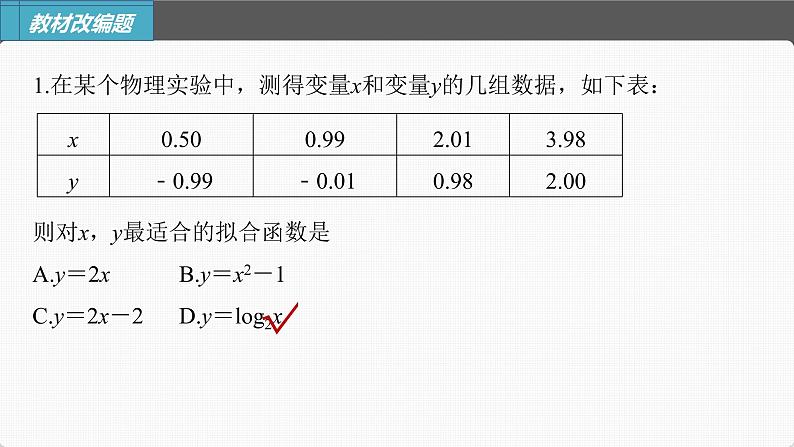
1.在某个物理实验中，测得变量x和变量y的几组数据，如下表：
则对x，y最适合的拟合函数是A.y＝2x B.y＝x2－1C.y＝2x－2 D.y＝lg2x
根据x＝0.50，y＝－0.99，代入计算，可以排除A；根据x＝2.01，y＝0.98，代入计算，可以排除B，C；将各数据代入函数y＝lg2x，可知满足题意.
2.设甲、乙两地的距离为a(a>0)，小王骑自行车匀速从甲地到乙地用了20分钟，在乙地休息10分钟后，他又匀速从乙地返回到甲地用了30分钟，则小王从出发到返回原地所经过的路程y和其所用的时间x的函数图象为
3.当生物死亡后，其体内原有的碳14的含量大约每经过5 730年衰减为原来的一半，这个时间称为“半衰期”.当死亡生物体内的碳14含量不足死亡前的千分之一时，用一般的放射性探测器就测不到了.若某死亡生物体内的碳14用该放射性探测器探测不到，则它至少要经过____个“半衰期”.
所以，若某死亡生物体内的碳14用该放射性探测器探测不到，则它至少需要经过10个“半衰期”.
TANJIUHEXINTIXING
例1　(1)如图，一高为H且装满水的鱼缸，其底部有一排水小孔，当小孔打开时，水从孔中匀速流出，水流完所用时间为T.若鱼缸水深为h时，水流出所用时间为t，则函数h＝f(t)的图象大致是
用函数图象刻画变化过程
水匀速流出，所以鱼缸水深h先降低快，中间降低缓慢，最后降低速度又越来越快.
(2)(2022·泰州模拟)中国茶文化博大精深，茶水的口感与茶叶类型和水的温度有关.经验表明，某种绿茶用85 ℃的水泡制，再等到茶水温度降至60 ℃时饮用，可以产生最佳口感.为分析泡制一杯最佳口感茶水所需时间，某研究人员每隔1 min测量一次茶水的温度，根据所得数据做出如图所示的散点图.观察散点图的分布情况，下列哪个函数模型可以近似地刻画茶水温度y随时间x变化的规律A.y＝mx2＋n(m>0)B.y＝max＋n(m>0,01)D.y＝mlgax＋n(m>0，a>0，a≠1)
由函数图象可知符合条件的只有指数函数模型，并且m>0,00)的值增加得越来越慢，由于凤眼莲在湖中的蔓延速度越来越快，故而函数模型y＝kax(k>0，a>1)满足要求.
(2)求凤眼莲的覆盖面积是元旦放入凤眼莲面积10倍以上的最小月份.(参考数据：lg 2≈0.301 0，lg 3≈0.477 1)
故x≥6.因此，凤眼莲覆盖面积是元旦放入凤眼莲面积10倍以上的最小月份是6月份.
11.(2022·衡阳模拟)“一骑红尘妃子笑，无人知是荔枝来”描述了封建统治者的骄奢生活，同时也讲述了古代资源流通的不便利.如今我国物流行业蓬勃发展，极大地促进了社会经济发展和资源整合.已知某类果蔬的保鲜时间y(单位：小时)与储藏温度x(单位：℃)满足函数关系y＝eax＋b(a，b为常数)，若该果蔬在6 ℃的保鲜时间为216小时，在24 ℃的保鲜时间为8小时，那么在12 ℃时，该果蔬的保鲜时间为A.72小时 B.36小时C.24小时 D.16小时
当x＝6时，e6a＋b＝216；
设甲同学的声强为I1，乙同学的声强为I2，
13.如图所示，一直角墙角，两边的长度足够长，在P处有一棵树与两墙的距离分别是a m(0