(新高考)高考数学一轮考点复习7.2《空间点、直线、平面之间的位置关系》学案 (含详解)

这是一份(新高考)高考数学一轮考点复习7.2《空间点、直线、平面之间的位置关系》学案 (含详解)，共17页。

第二节　空间点、直线、平面之间的位置关系
核心素养立意下的命题导向
1.理解空间直线、平面位置关系的定义，提升空间想象能力，凸显直观想象的核心素养．
2．了解可以作为推理依据的公理和定理，培养阅读理解能力，凸显数学抽象的核心素养．
3．能运用公理、定理和已获得的结论证明一些空间位置关系的简单命题，培养分析问题、解决问题的能力，凸显逻辑推理的核心素养．

[理清主干知识]
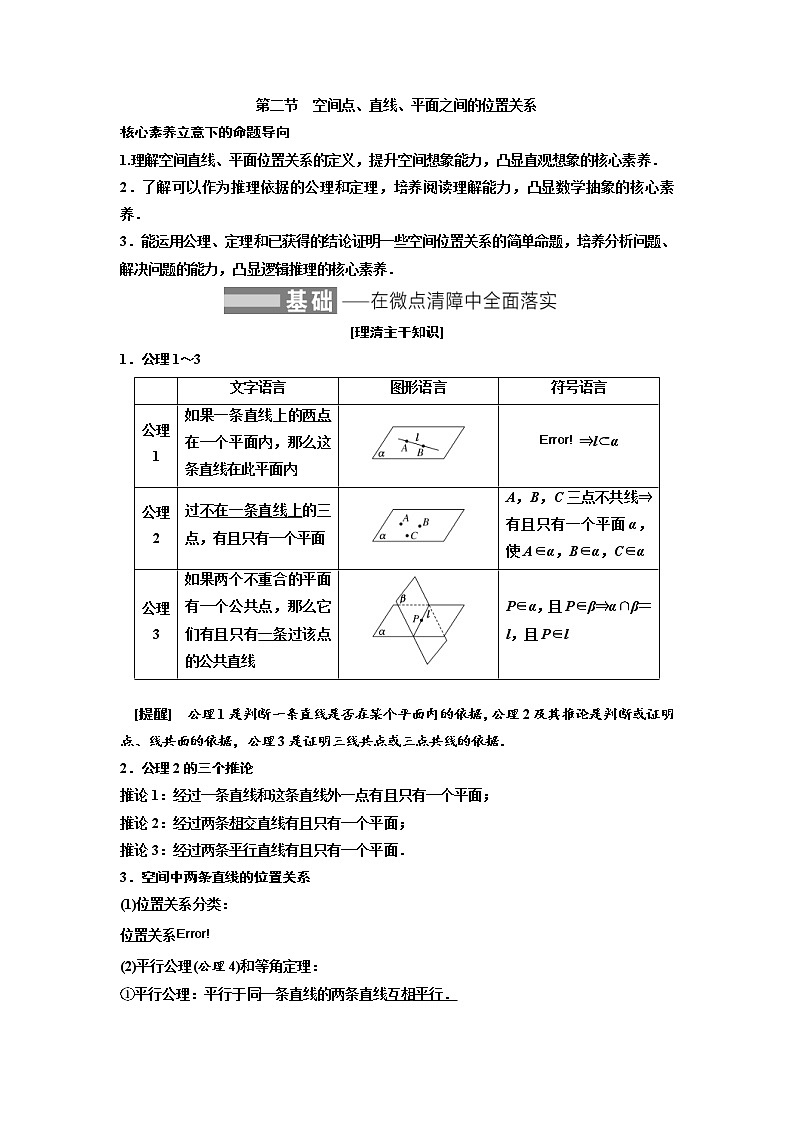
1．公理1～3

文字语言
图形语言
符号语言
公理1
如果一条直线上的两点在一个平面内，那么这条直线在此平面内

⇒l⊂α
公理2
过不在一条直线上的三点，有且只有一个平面

A，B，C三点不共线⇒有且只有一个平面α，使A∈α，B∈α，C∈α
公理3
如果两个不重合的平面有一个公共点，那么它们有且只有一条过该点的公共直线

P∈α，且P∈β⇒α∩β＝l，且P∈l

　[提醒]　公理1是判断一条直线是否在某个平面内的依据，公理2及其推论是判断或证明点、线共面的依据，公理3是证明三线共点或三点共线的依据．
2．公理2的三个推论
推论1：经过一条直线和这条直线外一点有且只有一个平面；
推论2：经过两条相交直线有且只有一个平面；
推论3：经过两条平行直线有且只有一个平面．
3．空间中两条直线的位置关系
(1)位置关系分类：
位置关系
(2)平行公理(公理4)和等角定理：
①平行公理：平行于同一条直线的两条直线互相平行．
②等角定理：空间中如果两个角的两边分别对应平行，那么这两个角相等或互补．
4．异面直线所成的角
(1)定义：已知两条异面直线a，b，经过空间任一点O作直线a′∥a，b′∥b，把a′与b′所成的锐角(或直角)叫做异面直线a与b所成的角(或夹角)．
(2)范围：.
5．空间中直线与平面、平面与平面的位置关系
(1)直线与平面的位置关系有相交、平行、在平面内三种情况．
(2)平面与平面的位置关系有平行、相交两种情况．
[澄清盲点误点]
一、关键点练明
1．(直线与直线的位置关系)已知a，b是异面直线，直线c平行于直线a，那么c与b(　　)
A．一定是异面直线　　　　 B．一定是相交直线
C．不可能是平行直线 D．不可能是相交直线
解析：选C　假设c∥b，又因为c∥a，所以a∥b，这与a，b是异面直线矛盾，故c与b不可能平行．
2．(确定平面的依据)下列命题正确的是(　　)
A．经过三点确定一个平面
B．经过一条直线和一个点确定一个平面
C．四边形确定一个平面
D．两两相交且不共点的三条直线确定一个平面
解析：选D　A选项考查公理2，即三点必须不在同一条直线上，才能确定一个平面；B选项如果点在直线上，则该直线和这个点不能确定一个平面；C选项中的四边形有可能是空间四边形，只有D是正确的．
3．(异面直线所成角)如图所示，在正方体ABCD­A1B1C1D1中，E，F分别是AB，AD的中点，则异面直线B1C与EF所成角的大小为(　　)
A．30° B．45°
C．60° D．90°
解析：选C　连接B1D1，D1C(图略)，则B1D1∥EF，故∠D1B1C为所求的角，又B1D1＝B1C＝D1C，
∴∠D1B1C＝60°.
4．(平面的基本性质及推论)已知空间四边形的两条对角线相互垂直，顺次连接四边中点的四边形一定是(　　)
A．梯形 B．矩形
C．菱形 D．正方形
解析：选B　如图所示，易证四边形EFGH为平行四边形，因为E，F分别为AB，BC的中点，所以EF∥AC，又FG∥BD，所以∠EFG或其补角为AC与BD所成的角，而AC与BD所成的角为90°，所以∠EFG＝90°，故四边形EFGH为矩形．
二、易错点练清
1．(误解异面直线的概念)下列关于异面直线的说法正确的是(　　)
A．若a⊂α，b⊂β，则a与b是异面直线
B．若a与b异面，b与c异面，则a与c异面
C．若a，b不同在平面α内，则a与b异面
D．若a，b不同在任何一个平面内，则a与b异面
解析：选D　A、B、C中的两条直线还有可能平行或相交，由异面直线的定义可知D说法正确．
2．(忽视直线在平面内)若直线a⊥b，且直线a∥平面α，则直线b与平面α的位置关系是(　　)
A．b⊂α B．b∥α
C．b⊂α或b∥α D．b与α相交或b⊂α或b∥α
解析：选D　将直线与平面放在正方体中，易知b与α相交或b⊂α或b∥α都可以．
3．(忽视异面直线所成角的范围)如图所示，已知在长方体ABCD­EFGH中，AB＝2，AD＝2，AE＝2，则BC和EG所成角的大小是________；AE和BG所成角的大小是________．
解析：∵BC与EG所成的角等于EG与FG所成的角，即∠EGF，tan∠EGF＝＝1，∴∠EGF＝45°.∵AE与BG所成的角等于BF与BG所成的角，即∠GBF，tan∠GBF＝＝＝，∴∠GBF＝60°.
答案：45°　60°

考点一　平面的基本性质及应用
[典例]　如图，在正方体ABCD­A1B1C1D1中，E，F分别是AB和AA1的中点．求证：
(1)E，C，D1，F四点共面；
(2)CE，D1F，DA三线共点．
[证明]　(1)如图所示，连接CD1，EF，A1B，因为E，F分别是AB和AA1的中点，
所以EF∥A1B且EF＝A1B.
又因为A1D1綊BC，
所以四边形A1BCD1是平行四边形，所以A1B∥CD1，
所以EF∥CD1，
所以EF与CD1确定一个平面α.
所以E，F，C，D1∈α，即E，C，D1，F四点共面．
(2)由(1)知EF∥CD1且EF＝CD1，
所以四边形CD1FE是梯形，
所以CE与D1F必相交，设交点为P，
则P∈CE⊂平面ABCD，
且P∈D1F⊂平面A1ADD1，
所以P∈平面ABCD，且P∈平面A1ADD1.
又因为平面ABCD∩平面A1ADD1＝AD，
所以P∈AD，所以CE，D1F，DA三线共点．
[方法技巧]
1．证明点或线共面问题的2种方法
(1)首先由所给条件中的部分线(或点)确定一个平面，然后再证其余的线(或点)在这个平面内；
(2)将所有条件分为两部分，然后分别确定平面，再证两平面重合．
2．证明点共线问题的2种方法
(1)先由两点确定一条直线，再证其他各点都在这条直线上；
(2)直接证明这些点都在同一条特定直线(如某两个平面的交线)上．
3．证明线共点问题的常用方法
先证其中两条直线交于一点，再证其他直线经过该点．　　
[针对训练]
1.如图所示，ABCD­A1B1C1D1是长方体，O是B1D1的中点，直线A1C交平面AB1D1于点M，则下列结论正确的是(　　)
A．A，M，O三点共线
B．A，M，O，A1不共面
C．A，M，C，O不共面
D．B，B1，O，M共面
解析：选A　连接A1C1，AC，则A1C1∥AC，
∴A1，C1，A，C四点共面，
∴A1C⊂平面ACC1A1，
∵M∈A1C，∴M∈平面ACC1A1，
又M∈平面AB1D1，
∴M在平面ACC1A1与平面AB1D1的交线上．
同理A，O在平面ACC1A1与平面AB1D1的交线上，
∴A，M，O三点共线．
2.如图，在空间四边形ABCD中，E，F分别是AB，AD的中点，G，H分别在BC，CD上，且BG∶GC＝DH∶HC＝1∶2.
(1)求证：E，F，G，H四点共面；
(2)设EG与FH交于点P，求证：P，A，C三点共线．
证明：(1)∵E，F分别为AB，AD的中点，∴EF∥BD.
∵在△BCD中，＝＝，
∴GH∥BD，∴EF∥GH.
∴E，F，G，H四点共面．
(2)∵EG∩FH＝P，
P∈EG，EG⊂平面ABC，
∴P∈平面ABC.同理P∈平面ADC.
∴P为平面ABC与平面ADC的公共点．
又平面ABC∩平面ADC＝AC，
∴P∈AC，∴P，A，C三点共线．
考点二　空间两条直线的位置关系
[典例]　(1)(多选)下列结论正确的是(　　)
A．在空间中，若两条直线不相交，则它们一定平行
B．平行于同一条直线的两条直线平行
C．一条直线和两条平行直线中的一条相交，那么它也和另一条相交
D．空间中四条直线a，b，c，d，如果a∥b，c∥d，且a∥d，那么b∥c
(2)已知α是一个平面，m，n是两条不同的直线，A是一个点，若m⊄α，n⊂α，且A∈m，A∈α，则m，n的位置关系不可能是(　　)
A．垂直　　　　　　　　 B．相交
C．异面 D．平行
[解析]　(1)若两条直线不相交，则它们可能平行，也可能异面，A错误；由公理4可知B正确；若一条直线和两条平行直线中的一条相交，则它和另一条直线可能相交，也可能异面，C错误；由平行直线的传递性可知D正确．故选B、D.
(2)∵α是一个平面，m，n是两条不同的直线，A是一个点，m⊄α，n⊂α，且A∈m，A∈α，∴A在平面α内，m与平面α相交．
∵A∈m，A∈α，∴A是m和平面α的交点，∴m和n异面或相交(特殊情况可垂直)，但一定不平行．
[答案]　(1)BD　(2)D
[方法技巧]　空间两直线位置关系的判定方法


[针对训练]
1．(多选)(2021年1月新高考八省联考卷)如图是一个正方体的平面展开图，则在该正方体中(　　)

A．AE∥CD
B．CH∥BE
C．DG⊥BH
D．BG⊥DE
解析：选BCD　还原正方体直观图如图，
可知AE与CD为异面直线，故选项A不正确；
由EH綊BC，可得CH∥BE，故选项B正确；
正方体中易得DG⊥平面BCH，所以有DG⊥BH，
故选项C正确；
因为BG∥AH且DE⊥AH，所以BG⊥DE，故选项D正确．
2．(多选)如图是正四面体的平面展开图，G，H，M，N分别为DE，BE，EF，EC的中点，则在这个正四面体中(　　)
A．GH与EF平行
B．BD与MN为异面直线
C．GH与MN成60°角
D．DE与MN垂直
解析：选BCD　还原成正四面体A­DEF如图所示，其中H与N重合，A，B，C三点重合，易知GH与EF异面，BD与MN异面．连接GM，∵△GMH为等边三角形，∴GH与MN成60°角．由图易得DE⊥AF，又MN∥AF，∴MN⊥DE，因此正确的选项是B、C、D.
考点三　异面直线所成的角
[典例]　(1)在正三棱柱ABC­A1B1C1中，若AA1＝2AB，D是AA1的中点，则BD与A1C1所成角的余弦值为(　　)
A.　　　　　　　　　 B.
C. D.
(2)(2021·岳阳联考)在四面体ABCD中，BD⊥AD，CD⊥AD，BD⊥BC，BD＝AD＝1，BC＝2，则异面直线AB与CD所成角的余弦值为(　　)
A. B.
C. D.
[解析]　(1)如图，取CC1的中点M，连接DM，BM.由于D为AA1的中点，所以DM∥A1C1，所以∠BDM或其补角为异面直线BD与A1C1所成的角．设AA1＝2AB＝2，则AD＝AB＝1.因为三棱柱ABC­A1B1C1为正三棱柱，所以BD＝，DM＝1，BM＝.
在△BDM中，cos∠BDM＝＝
＝，故选B.
(2)如图，在平面BCD内，过点D作BC的平行线与过点B所作CD的平行线相交于E，连接AE，则四边形BCDE为平行四边形，所以DE＝BC＝2，且∠ABE或其补角为异面直线AB与CD所成的角．因为AD⊥BD，AD⊥CD，BD∩CD＝D，所以AD⊥平面BCD，则AD⊥DE，所以AE＝＝，易知AB＝＝.因为BD⊥BC，所以DC＝＝，则BE＝CD＝，于是在△ABE中，由余弦定理，
得cos∠ABE＝＝＝，
故选D.
[答案]　(1)B　(2)D
[方法技巧]　平移法求异面直线所成角的步骤
平移
平移的方法一般有三种类型：(1)利用图中已有的平行线平移；(2)利用特殊点(线段的端点或中点)作平行线平移；(3)补形平移
证明
证明所作的角是异面直线所成的角或其补角
寻找
在立体图形中，寻找或作出含有此角的三角形，并解之
取舍
因为异面直线所成角θ的取值范围是0°＜θ≤90°，所以所作的角为钝角时，应取它的补角作为异面直线所成的角

[针对训练]
1．在长方体ABCD­A1B1C1D1中，AB＝1，AD＝2，AA1＝3，则异面直线A1B1与AC1所成角的余弦值为(　　)
A. B.
C. D.
解析：选A　∵C1D1∥A1B1，∴异面直线A1B1与AC1所成的角即为C1D1与AC1所成的角，即∠AC1D1或其补角．
连接AD1，易知AD1⊥C1D1.∵在Rt△AC1D1中，C1D1＝1，AD1＝＝，AC1＝＝，∴cos∠AC1D1＝＝＝.
2．已知A，B两点都在以PC为直径的球O的表面上，AB⊥BC，AB＝2，BC＝4.若球O的体积为8π，则异面直线PB与AC所成角的余弦值为________．
解析：由题意得三棱锥P­ABC，如图所示，其中PA⊥AC，PB⊥BC，AB⊥BC.
过点A作BC的平行线，过点B作AC的平行线，两线交于点D，
则异面直线PB与AC所成角为∠PBD(或其补角)．
由PB⊥BC，AB⊥BC，PB∩AB＝B，得BC⊥平面PAB，即BC⊥PA，又PA⊥AC，BC∩AC＝C，
∴PA⊥平面ACBD，∴PA⊥AD.
计算可得AC＝2＝BD，
设球O的半径为R，则πR3＝8π，
∴R＝，PC＝2，∴PA＝2，
∴PB＝2，PD＝2.
取PB的中点E，连接DE，∵PD＝BD，∴DE⊥PB，
∴cos∠PBD＝＝＝，
即异面直线PB与AC所成角的余弦值为.
答案：


创新思维角度——融会贯通学妙法
异面直线所成角的解法探究
[典例]　正方体ABCD­A1B1C1D1中，P为BC1的中点，Q为A1D的中点，则异面直线DP与C1Q所成角的余弦值为________．
[思路点拨]　在正方体中求异面直线所成角的余弦值，考虑到正方体的特征，可以用平移直线法求解；或建立空间直角坐标系，利用坐标法求解；或利用基向量法求解；或利用三余弦定理法求解．
[解析]　法一：平移直线法
如图所示，连接CB1，QB1，
因为四边形BCC1B1为正方形，P为BC1的中点，所以B1P＝B1C.
因为A1B1∥CD且A1B1＝CD，
所以四边形CDA1B1为平行四边形，
所以B1C∥A1D且B1C＝A1D，
又Q为A1D的中点，所以B1P∥QD且B1P＝QD，
所以四边形DPB1Q为平行四边形，所以B1Q∥DP，
所以∠B1QC1或其补角为异面直线DP与C1Q所成的角．
设正方体的棱长为2，在Rt△B1A1Q中，
B1Q＝＝＝；
同理可得C1Q＝.
在△B1C1Q中，cos∠B1QC1＝＝＝，
故异面直线DP与C1Q所成角的余弦值为.
法二：坐标法
以D为坐标原点，分别以，，的方向为x轴、y轴、z轴的正方向，建立如图所示的空间直角坐标系D­xyz.
设正方体的棱长为2，则各点的坐标为D(0,0,0)，P(1,2,1)，Q(1,0,1)，C1(0,2,2)，
所以＝(1,2,1)，＝(1，－2，－1)，
所以cos〈，〉＝＝＝－.
所以异面直线DP与C1Q所成角的余弦值为.
法三：基向量法
设正方体的棱长为2，＝a，＝b，＝c，
则＝b＋(a＋c)＝a＋b＋c，
＝－b＋(a－c)＝a－b－c.
由直线DA，DC，DD1两两垂直得a·b＝b·c＝a·c＝0，
所以·＝2－2
＝a2－b2－c2＝×22－22－×22＝－4，
||＝ ＝，
||＝ ＝，
所以cos〈，〉＝＝＝－.
所以异面直线DP与C1Q所成角的余弦值为.
法四：三余弦定理法
如图所示，连接AD1，PQ，AP，B1C，易知四边形ABC1D1为平行四边形，且DQ⊥平面ABC1D1，
即PQ为DP在平面ABC1D1上的射影，
易知AP∥C1Q，所以∠APD或其补角为异面直线DP与C1Q所成的角．
设正方体的棱长为1，
易知cos∠APQ＝，cos∠DPQ＝，
由三余弦定理得cos∠APD＝cos∠APQ×cos∠DPQ＝×＝，
即异面直线DP与C1Q所成角的余弦值为.
[答案]　

法一可通过平行四边形找平行线达到平移的目的，将两条异面直线所成的角转化为两条相交直线所成的角求解，这时往往将平移后的角置于一个三角形中，通过解三角形获得角的三角函数值；法二可考虑到当载体是正方体或长方体时，建立空间直角坐标系，利用坐标去求角，这种方法往往比较简单；法三也可以利用空间向量基本定理，选取一组基向量，然后利用基向量解决其他向量的夹角问题．　　
[方法提炼]　
两条异面直线所成角的求法
(1)利用平移直线法求解的实质就是将空间两直线所成角转化为平面三角形的内角去求解．
(2)向量法有两种，一是建立空间直角坐标系，利用坐标结合向量数量积的性质求解，二是利用基向量结合向量数量积的性质求解．
(3)三余弦定理法的关键是找到两条异面直线中的一条在包含另一条直线的平面内的射影．
如图所示，OA是与平面α相交的一条斜线，OA在平面α内的射影为AB，AC是平面α内的一条直线，∠OAC＝θ，∠OAB＝θ1，∠BAC＝θ2，则cos θ＝cos θ1cos θ2.

一、基础练——练手感熟练度
1．(多选)下列推断中，正确的是(　　)
A．A∈l，A∈α，B∈l，B∈α⇒l⊂α
B．A∈α，A∈β，B∈α，B∈β⇒α∩β＝AB
C．l⊄α，A∈l⇒A∉α
D．A，B，C∈α，A，B，C∈β，且A，B，C不共线⇒α，β重合
解析：选ABD　直线不在平面内时，直线上可能有一个点在平面内，即直线与平面相交，所以C错，根据点、线、面的关系可知其余都对，故选A、B、D.
2．已知直线a和平面α，β，α∩β＝l，a⊄α，a⊄β，且a在α，β内的射影分别为直线b和c，则直线b和c的位置关系是(　　)
A．相交或平行　　　　　 B．相交或异面
C．平行或异面 D．相交、平行或异面
解析：选D　依题意，直线b和c的位置关系可能是相交、平行或异面，选D.
3．下列命题中，错误命题的个数为(　　)
①直线a与平面α不平行，则直线a与平面α内的所有直线都不平行；
②直线a与平面α不垂直，则直线a与平面α内的所有直线都不垂直；
③异面直线a，b不垂直，则过直线a的任何平面与直线b都不垂直；
④若直线a和b共面，直线b和c共面，则直线a和c共面．
A．1 B．2
C．3 D．4
解析：选C　对于①，若直线a在平面α内，这时直线a和平面α不平行，但是平面内存在直线和a是平行的，故①错误；对于②，若直线a在平面α内，这时直线a和平面α不垂直，但是平面内存在直线和直线a是垂直的，故②错误；对于③，根据线面垂直的定义可知，③是正确的；对于④，直线a，c有可能是异面直线，故④错误．综上所述，有3个命题是错误命题，故选C.
4．如果两条异面直线称为“一对”，那么在正方体的十二条棱中共有异面直线(　　)
A．12对 B．24对
C．36对 D．48对
解析：选B　如图所示，与AB异面的直线有B1C1，CC1，A1D1，DD1四条，因为各棱具有相同的位置且正方体共有12条棱，排除两棱的重复计算，共有异面直线＝24(对)．
5．已知A，B，C，D是空间四点，命题甲：A，B，C，D四点不共面，命题乙：直线AC和BD不相交，则甲是乙成立的(　　)
A．充分不必要条件 B．必要不充分条件
C．充要条件 D．既不充分也不必要条件
解析：选A　若A，B，C，D四点不共面，则直线AC和BD不共面，所以AC和BD不相交；若直线AC和BD不相交，当直线AC和BD平行时，A，B，C，D四点共面，所以甲是乙成立的充分不必要条件．
6.(2021·临沂模拟)如图，四边形ABCD和四边形ADPQ均为正方形，它们所在的平面互相垂直，则异面直线AP与BD所成的角为________．
解析：

如图，将原图补成正方体ABCD­QGHP，连接GP，则GP∥BD，所以∠APG为异面直线AP与BD所成的角，在△AGP中，AG＝GP＝AP，
所以∠APG＝.
答案：

二、综合练——练思维敏锐度
1．(2021·威海一中月考)设α，β为不重合的两个平面，m，n为不重合的两条直线，则下列命题正确的是(　　)
A．若α⊥β，α∩β＝n，m⊥n，则m⊥α
B．若m⊂α，n⊂β，m∥n，则α∥β
C．若m∥α，n∥β，m⊥n，则α⊥β
D．若n⊥α，n⊥β，m⊥β，则m⊥α
解析：选D　对于A，若α⊥β，α∩β＝n，m⊥n，则m与α有可能相交，也有可能m⊂α，故A错误；对于B，若m⊂α，n⊂β，m∥n，则α与β有可能相交，也有可能平行，故B错误；对于C，若m∥α，n∥β，m⊥n，则α与β有可能平行，也有可能相交，故C错误；对于D，由于m⊥β，n⊥β，所以m∥n，又知n⊥α，所以m⊥α，故D正确．故选D.
2．若m，n是两条不同的直线，α，β，γ是三个不同的平面，则下列说法中正确的是(　　)
A．α∥β，m⊂α，n⊂β ⇒m∥n
B．α⊥γ，β⊥γ ⇒α∥β
C．α∥β，m∥n，m⊥α⇒n⊥β
D．α∩β＝m，β∩γ＝n，m∥n⇒α∥γ
解析：选C　对于A，由α∥β，m⊂α，n⊂β，可知m，n无公共点，则m与n平行或异面，故A错误；对于B，由α⊥γ，β⊥γ，可知α与β可能平行，也可能相交，故B错误；对于C，由于m∥n，m⊥α，所以n⊥α，又知α∥β，所以n⊥β，故C正确；对于D，如图所示，α∩β＝m，β∩γ＝n，m∥n，但α与γ相交，故D错误．故选C.
3.如图，在底面为正方形，侧棱垂直于底面的四棱柱ABCD­A1B1C1D1中，AA1＝2AB＝2，则异面直线A1B与AD1所成角的余弦值为(　　)
A. B.
C. D.
解析：选D　连接BC1，易证BC1∥AD1，则∠A1BC1(或其补角)即为异面直线A1B与AD1所成的角．
连接A1C1，由AB＝1，AA1＝2，则A1C1＝，A1B＝BC1＝，
在△A1BC1中，由余弦定理得cos∠A1BC1＝＝.
4．若平面α，β的公共点多于两个，则
①α，β平行；②α，β至少有三个公共点；③α，β至少有一条公共直线；④α，β至多有一条公共直线．
以上四个判断中不成立的个数为(　　)
A．0　　 B．1 C．2　　　　 D．3
解析：选C　由条件知，当平面α，β的公共点多于两个时，若所有公共点共线，则α，β相交；若公共点不共线，则α，β重合．故①一定不成立；②成立；③成立；④不成立．
5．(2021·沈阳模拟)如图，在三棱柱ABC­A1B1C1中，侧棱AA1⊥底面A1B1C1，底面三角形A1B1C1是正三角形，E是BC的中点，则下列叙述正确的是(　　)
A．CC1与B1E是异面直线
B．AC⊥平面ABB1A1
C．AE，B1C1为异面直线且AE⊥B1C1
D．A1C1∥平面AB1E
解析：选C　CC1与B1E在同一个侧面中，故不是异面直线，所以A错误；由题意知，上底面是一个正三角形，故AC不可能垂直于平面ABB1A1，所以B错误；因为AE，B1C1为在两个平行平面中且不平行的两条直线，故它们是异面直线，且因为△ABC为正三角形，点E为BC中点，所以AE⊥BC，又因为BC∥B1C1，所以AE⊥B1C1，所以C正确；因为A1C1所在的平面A1B1C1与平面AB1E相交，且A1C1与交线有公共点，故A1C1∥平面AB1E不正确，所以D错误．故选C.
6．(多选)(2021·日照模拟)如图，在长方体ABCD­A1B1C1D1中，AA1＝AB＝4，BC＝2，M，N分别为棱C1D1，CC1的中点，则(　　)
A．A，M，N，B四点共面
B．平面ADM⊥平面CDD1C1
C．直线BN与B1M所成的角为60°
D．BN∥平面ADM
解析：选BC　如图所示，对于A，直线AM，BN是异面直线，故A，M，N，B四点不共面，故A错误；对于B，在长方体ABCD­A1B1C1D1中，可得AD⊥平面CDD1C1，所以平面ADM⊥平面CDD1C1，故B正确；对于C，取CD的中点O，连接BO，ON，可知三角形BON为等边三角形，故C正确；对于D，因为BN∥平面AA1D1D，显然BN与平面ADM不平行，故D错误．故选B、C.
7.如图，已知圆柱的轴截面ABB1A1是正方形，C是圆柱下底面弧AB的中点，C1是圆柱上底面弧A1B1的中点，那么异面直线AC1与BC所成角的正切值为________．


解析：如图，取圆柱下底面弧AB的另一中点D，连接C1D，AD，
∵C是圆柱下底面弧AB的中点，
∴AD∥BC，
∴直线AC1与AD所成的角即为异面直线AC1与BC所成的角．
∵C1是圆柱上底面弧A1B1的中点，
∴C1D⊥圆柱下底面，∴C1D⊥AD.
∵圆柱的轴截面ABB1A1是正方形，
∴C1D＝AB＝AD，
∴直线AC1与AD所成角的正切值为，
∴异面直线AC1与BC所成角的正切值为.
答案：
8.如图，在正方体ABCD­A1B1C1D1中，M，N分别为棱C1D1，C1C的中点，有以下四个结论：
①直线AM与CC1是相交直线；
②直线AM与BN是平行直线；
③直线BN与MB1是异面直线；
④直线AM与DD1是异面直线．
其中正确的结论为________(填序号)．
解析：直线AM与CC1是异面直线，直线AM与BN也是异面直线，故①②错误．
答案：③④
9．(2021·洛阳模拟)如图，在三棱锥A­BCD中，AB＝AC＝BD＝CD＝3，AD＝BC＝2，点M，N分别为AD，BC的中点，则异面直线AN，CM所成角的余弦值是________．
解析：如图所示，连接DN，
取线段DN的中点K，连接MK，CK.
∵M为AD的中点，∴MK∥AN，
∴∠KMC(或其补角)为异面直线AN，CM所成的角．
∵AB＝AC＝BD＝CD＝3，AD＝BC＝2，N为BC的中点，
由勾股定理易求得AN＝DN＝CM＝2，∴MK＝.
在Rt△CKN中，CK＝ ＝.
在△CKM中，由余弦定理，
得cos∠KMC＝＝，
∴异面直线AN，CM所成角的余弦值是.
答案：
10．已知在直三棱柱ABC­A1B1C1中，∠ACB＝90°，AC＝2，BC＝CC1＝，P是BC1上一动点，则A1P＋PC的最小值为________．
解析：如图①，连接A1B，由已知数据可得BC1＝2，A1B＝2，则A1C＋BC＝A1B2，∴∠A1C1B＝90°.将△BCC1沿BC1展平在平面A1BC1内，连接A1C，如图②，则A1P＋PC的最小值为线段A1C的长．在△A1C1C中，A1C1＝2，CC1＝，易知∠A1C1C＝135°，由余弦定理得，A1C2＝A1C＋CC－2A1C1·CC1·cos∠A1C1C＝22＋()2－2×2××cos 135°＝4＋2＋4＝10，∴A1C＝，即A1P＋PC的最小值为.

答案：
11.如图，在四棱锥O­ABCD中，底面ABCD是边长为2的正方形，OA⊥底面ABCD，OA＝2，M为OA的中点．
(1)求四棱锥O­ABCD的体积；
(2)求异面直线OC与MD所成角的正切值．
解：(1)由已知可求得正方形ABCD的面积S＝4，
∴四棱锥O­ABCD的体积V＝×4×2＝.
(2)如图，连接AC，设线段AC的中点为E，连接ME，DE，又M为OA的中点，
∴ME∥OC，
则∠EMD(或其补角)为异面直线OC与MD所成的角，由已知可得DE＝，EM＝，MD＝，
∵()2＋()2＝()2，即DE2＋EM2＝MD2，
∴△DEM为直角三角形，且∠DEM＝90°，
∴tan∠EMD＝＝＝.
∴异面直线OC与MD所成角的正切值为.
12.如图所示，A是△BCD所在平面外的一点，E，F分别是BC，AD的中点．
(1)求证：直线EF与BD是异面直线；
(2)若AC⊥BD，AC＝BD，求EF与BD所成的角的大小．
解：(1)证明：假设EF与BD不是异面直线，则EF与BD共面，从而DF与BE共面，即AD与BC共面，
所以A，B，C，D在同一平面内，这与A是△BCD所在平面外的一点相矛盾，故直线EF与BD是异面直线．
(2)如图，取CD的中点G，连接EG，FG，
则AC∥FG，EG∥BD.
所以相交直线EF与EG所成的角即为异面直线EF与BD所成的角．
又因为AC⊥BD，则FG⊥EG，
在Rt△EGF中，由EG＝FG＝AC，求得∠FEG＝45°，即异面直线EF与BD所成的角为45°.