河北省沧州市东光县东光县于桥乡初级中学2022-2023学年八年级上学期10月月考数学试题(含答案)

这是一份河北省沧州市东光县东光县于桥乡初级中学2022-2023学年八年级上学期10月月考数学试题(含答案)，共12页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1.以长为13cm、10cm、5cm、7cm的四条线段中的三条线段为边，可以画出三角形的个数是（ ）
A．1个B．2个C．3个D．4个
2.如图，在△ABC中，D，E分别为BC上两点，且BD=DE=EC，则图中面积相等的三角形有（ ）对．
A．4B．5C．6D．7
3.如图，△ABC的角平分线BD与中线CE相交于点O．有下列两个结论：
①BO是△CBE的角平分线；②CO是△CBD的中线．
其中（ ）
A．只有①正确B．只有②正确C．①和②都正确D．①和②都不正确
4.如图，直线a、b、c、d互不平行，对它们截出的一些角的数量关系描述错误的是（ ）
A．∠1+∠6﹦∠2B．∠4+∠5﹦∠2
C．∠1+∠3+∠6﹦180°D．∠1+∠5+∠4﹦180°
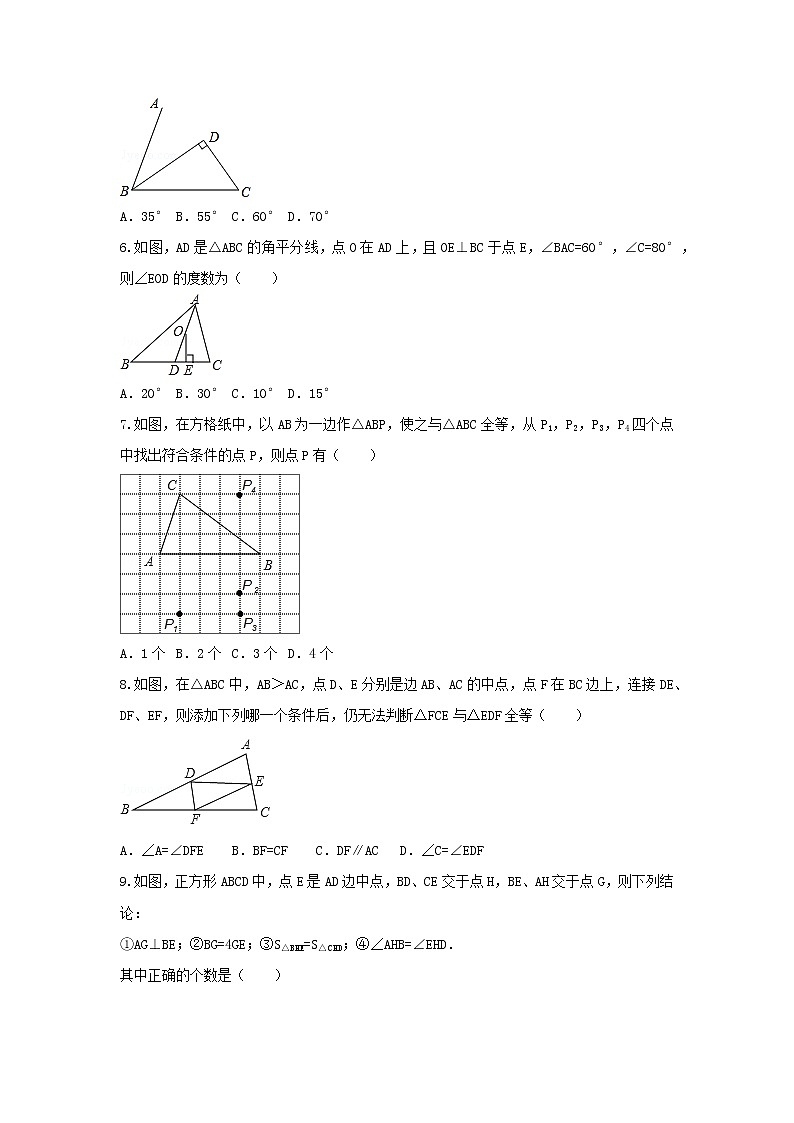
5.如图，BD平分∠ABC，CD⊥BD，D为垂足，∠C=55°，则∠ABC的度数是（ ）
A．35°B．55°C．60°D．70°
6.如图，AD是△ABC的角平分线，点O在AD上，且OE⊥BC于点E，∠BAC=60°，∠C=80°，则∠EOD的度数为（ ）
A．20°B．30°C．10°D．15°
7.如图，在方格纸中，以AB为一边作△ABP，使之与△ABC全等，从P1，P2，P3，P4四个点中找出符合条件的点P，则点P有（ ）
A．1个B．2个C．3个D．4个
8.如图，在△ABC中，AB＞AC，点D、E分别是边AB、AC的中点，点F在BC边上，连接DE、DF、EF，则添加下列哪一个条件后，仍无法判断△FCE与△EDF全等（ ）
A．∠A=∠DFEB．BF=CFC．DF∥ACD．∠C=∠EDF
9.如图，正方形ABCD中，点E是AD边中点，BD、CE交于点H，BE、AH交于点G，则下列结论：
①AG⊥BE；②BG=4GE；③S△BHE=S△CHD；④∠AHB=∠EHD．
其中正确的个数是（ ）
A．1B．2C．3D．4
10.如图，点P是∠AOB平分线OC上一点，PD⊥OB，垂足为D，若PD＝2，则点P到边OA的距离是( )
A．1
B．2
C.eq \r(3)
D．4
11.如图，AD是△ABC的角平分线，DF⊥AB，垂足为F，DE＝DG，△ADG和△AED的面积分别为27和16，则△EDF的面积为( )
A．11 B．5.5 C．7 D．3.5
12.如图，已知AB＝DC，AD＝BC，E，F是DB上两点且BF＝DE，若∠AEB＝100°，∠ADB＝30°，则∠BCF的度数为( )
A．150° B．40° C．80° D．70°
13.在△ABC和△A′B′C′中，有下列条件：①AB＝A′B′；②BC＝B′C′；③AC＝A′C′；④∠A＝∠A′；⑤∠B＝∠B′；⑥∠C＝∠C′，则以下各组条件中不能保证△ABC≌△A′B′C′的一组是( )
A．①②③ B．①②⑤ C．①③⑤ D．②⑤⑥
14.如图，在△ABC中，∠C=90°，点D，E分别在边AC，AB上．若∠B=∠ADE，则下列结论正确的是（ ）
A．∠A和∠B互为补角B．∠B和∠ADE互为补角
C．∠A和∠ADE互为余角D．∠AED和∠DEB互为余角
15.如图，若∠A=27°，∠B=45°，∠C=38°，则∠DFE等于（ ）
A．120°B．115°C．110°D．105°
二、填空题（每题2分，共20分）
16.已知a，b，c是三角形的三边长，化简：|a﹣b+c|﹣|a﹣b﹣c|=
17.如图，∠A+∠B+∠C+∠D+∠E+∠F= 度．
18.如图，一副三角板△AOC和△BCD如图摆放，则∠AOB= ．
19.如图，在△ABC中，∠B=46°，∠C=54°，AD平分∠BAC，交BC于D，DE∥AB，交AC于E，则∠ADE的大小是 ．
20.如图，△ABC中，∠ACB＞90°，AD⊥BC，BE⊥AC，CF⊥AB，垂足分别为D、E、F，则线段 是△ABC中AC边上的高．
21.如图，在正方形ABCD中，如果AF=BE，那么∠AOD的度数是
22.如图，要测量池塘的宽度AB，在池塘外选取一点P，连接AP，BP并各自延长，使PC＝PA，PD＝PB，连接CD，测得CD长为25 m，则池塘宽AB为________m
23.如图，在Rt△ABC中，∠C＝90°，AC＝10，BC＝5，线段PQ＝AB，P，Q两点分别在AC和过点A且垂直于AC的射线AO上运动，当AP＝________时，△ABC和△PQA全等．
24.如图，AD＝AE，BE＝CD，∠1＝∠2＝110°，∠BAC＝80°，则∠CAE的度数是________．
如图，点D，B，C点在同一条直线上，∠A=60°，∠C=50°，∠D=25°，则∠1=
度．
四、解答题
26.（6分）如图所示，直线AD和BC相交于O，AB∥CD，∠AOC=95°，∠B=50°，求∠A和∠D．
27.（6分）如图△ABC中，∠A=20°，CD是∠BCA的平分线，△CDA中，DE是CA边上的高，又有∠EDA=∠CDB，求∠B的大小．
28.（8分）如图，点C是AE的中点，∠A＝∠ECD，AB＝CD，ED＝4，求CB的长度．
29.（8分）已知△ABN和△ACM的位置如图所示，AB＝AC，AD＝AE，∠1＝∠2.
(1)求证BD＝CE；
(2)求证∠M＝∠N.
30.（10分）如图，四边形ABCD，BEFG均为正方形，连接AG，CE.求证：
(1)AG＝CE；
(2)AG⊥CE.
31.（12分）如图①，在△ABC中，∠ACB是直角，∠B＝60°，AD，CE分别是∠BAC，∠BCA的平分线，AD，CE相交于点F.
(1)请你判断并写出FE与FD之间的数量关系(不需证明)．
(2)如图②，如果∠ACB不是直角，其他条件不变，那么在(1)中所得的结论是否仍然成立？若成立，请证明；若不成立，请说明理由．
答案
一、选择题
1-5.CAAAD 6-10.ACADB 11-15.BDCCC
二、填空题
16.2a﹣2b
17.360
18.165°
19.40°
20.BE
21.90°
22.25
23.5或10
24.20°
25.45
三、解答题
26.解：在△ABO中，∵∠AOC=95°，∠B=50°，
∴∠A=∠AOC﹣∠B=95°﹣50°=45°；
∵AB∥CD，
∴∠D=∠A=45°．
27.解：∵DE是CA边上的高，
∴∠DEA=∠DEC=90°，
∵∠A=20°，
∴∠EDA=90°﹣20°=70°，
∵∠EDA=∠CDB，
∴∠CDE=180°﹣70°×2=40°，
在Rt△CDE中，∠DCE=90°﹣40°=50°，
∵CD是∠BCA的平分线，
∴∠BCA=2∠DCE=2×50°=100°，
在△ABC中，∠B=180°﹣∠BCA﹣∠A=180°﹣100°﹣20°=60°．
故答案为：60°．
28.解：∵点C是AE的中点，
∴AC＝CE.
在△ABC和△CDE中，
eq \b\lc\{(\a\vs4\al\c1(AC＝CE，,∠A＝∠ECD，,AB＝CD，))
∴△ABC≌△CDE(SAS)，
∴ED＝CB.
又∵ED＝4，∴CB＝4.
29.证明：(1)在△ABD和△ACE中，
eq \b\lc\{(\a\vs4\al\c1(AB＝AC，,∠1＝∠2，,AD＝AE，))
∴△ABD≌△ACE(SAS)．
∴BD＝CE.
(2)∵∠1＝∠2，
∴∠1＋∠DAE＝∠2＋∠DAE，
即∠BAN＝∠CAM，
由(1)知△ABD≌△ACE，
∴∠B＝∠C，
在△ACM和△ABN中，
eq \b\lc\{(\a\vs4\al\c1(∠C＝∠B，,AC＝AB，,∠CAM＝∠BAN，))
∴△ACM≌△ABN(ASA)．
∴∠M＝∠N.
30.证明：(1)∵四边形ABCD，BEFG均为正方形，∴AB＝CB，∠ABC＝∠GBE＝90°，BG＝BE.∴∠ABG＝∠CBE.在△ABG和△CBE中，
eq \b\lc\{(\a\vs4\al\c1(AB＝CB，,∠ABG＝∠CBE，,BG＝BE，))
∴△ABG≌△CBE(SAS)，
∴AG＝CE.
(2)设AG与BC的交点为M，AG与CE的交点为N，由(1)可知△ABG≌△CBE，
∴∠BAG＝∠BCE.∵∠ABC＝90°，
∴∠BAG＋∠AMB＝90°.又∵∠AMB＝∠CMN，∴∠BCE＋∠CMN＝90°.
∴∠CNM＝90°，∴AG⊥CE.
31.解：(1)FE＝FD.
(2)成立．证明：如图，在AC上取AG＝AE，连接FG.
(第24题)
∵∠B＝60°，AD，CE分别平分∠BAC，∠BCA，
∴∠1＝∠2，∠3＝∠4，∠1＋∠2＋∠3＋∠4＝120°.
∴∠2＋∠3＝60°.
在△AEF和△AGF中，
eq \b\lc\{(\a\vs4\al\c1(AE＝AG，,∠1＝∠2，,AF＝AF，))
∴△AEF≌△AGF(SAS)．
∴∠AFE＝∠AFG，FE＝FG.
∵∠AFE＝∠CFD＝∠2＋∠3＝60°，
∴∠AFG＝∠AFE＝60°.
∴∠CFG＝60°.
在△CFG和△CFD中，
eq \b\lc\{(\a\vs4\al\c1(∠CFG＝∠CFD＝60°，,CF＝CF，,∠3＝∠4，))
∴△CFG≌△CFD(ASA)．
∴FG＝FD.
∴FE＝FD.