陕西西安市爱知中学2021-2022学年初中数学毕业考试模拟冲刺卷含解析

这是一份陕西西安市爱知中学2021-2022学年初中数学毕业考试模拟冲刺卷含解析，共24页。试卷主要包含了函数y=中自变量x的取值范围是，济南市某天的气温等内容，欢迎下载使用。

2021-2022中考数学模拟试卷
注意事项：
1． 答题前，考生先将自己的姓名、准考证号填写清楚，将条形码准确粘贴在考生信息条形码粘贴区。
2．选择题必须使用2B铅笔填涂；非选择题必须使用0．5毫米黑色字迹的签字笔书写，字体工整、笔迹清楚。
3．请按照题号顺序在各题目的答题区域内作答，超出答题区域书写的答案无效；在草稿纸、试题卷上答题无效。
4．保持卡面清洁，不要折叠，不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。

一、选择题（共10小题，每小题3分，共30分）
1．目前，世界上能制造出的最小晶体管的长度只有0.000 000 04m，将0.000 000 04用科学记数法表示为（　　）
A．0.4×108 B．4×108 C．4×10﹣8 D．﹣4×108
2．如图，等腰直角三角形位于第一象限，，直角顶点在直线上，其中点的横坐标为，且两条直角边，分别平行于轴、轴，若反比例函数的图象与有交点，则的取值范围是（ ）．

A． B． C． D．
3．在如图所示的计算程序中，y与x之间的函数关系所对应的图象应为（ ）

A． B． C． D．
4．如图是二次函数的部分图象，由图象可知不等式的解集是（ ）

A． B． C．且 D．x＜－1或x＞5
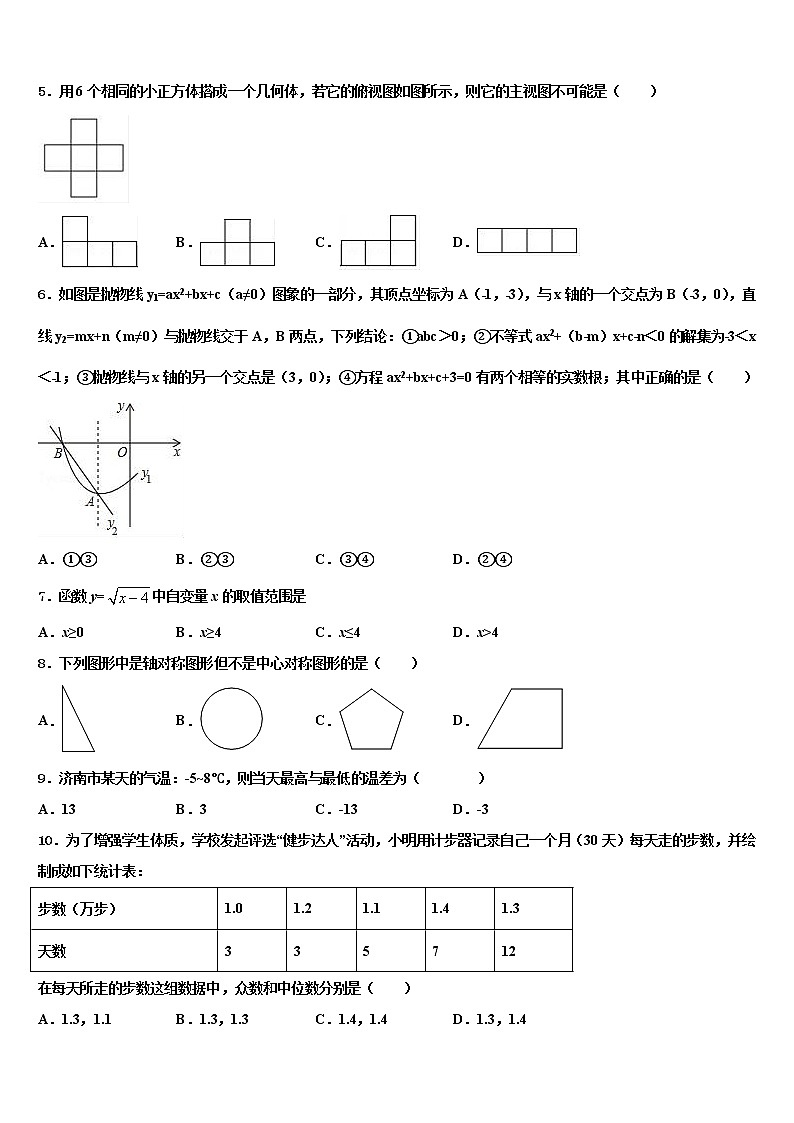
5．用6个相同的小正方体搭成一个几何体，若它的俯视图如图所示，则它的主视图不可能是（　　）

A． B． C． D．
6．如图是抛物线y1=ax2+bx+c（a≠0）图象的一部分，其顶点坐标为A（﹣1，﹣3），与x轴的一个交点为B（﹣3，0），直线y2=mx+n（m≠0）与抛物线交于A，B两点，下列结论：①abc＞0；②不等式ax2+（b﹣m）x+c﹣n＜0的解集为﹣3＜x＜﹣1；③抛物线与x轴的另一个交点是（3，0）；④方程ax2+bx+c+3=0有两个相等的实数根；其中正确的是（　　）

A．①③ B．②③ C．③④ D．②④
7．函数y=中自变量x的取值范围是
A．x≥0 B．x≥4 C．x≤4 D．x>4
8．下列图形中是轴对称图形但不是中心对称图形的是（　　）
A． B． C． D．
9．济南市某天的气温：-5~8℃，则当天最高与最低的温差为（ ）
A．13 B．3 C．-13 D．-3
10．为了增强学生体质，学校发起评选“健步达人”活动，小明用计步器记录自己一个月（30天）每天走的步数，并绘制成如下统计表：
步数（万步）
1.0
1.2
1.1
1.4
1.3
天数
3
3
5
7
12
在每天所走的步数这组数据中，众数和中位数分别是（　　）
A．1.3，1.1 B．1.3，1.3 C．1.4，1.4 D．1.3，1.4
二、填空题（本大题共6个小题，每小题3分，共18分）
11．计算：___________.
12．如图，在等腰直角三角形ABC中，∠C=90°，点D为AB的中点，已知扇形EAD和扇形FBD的圆心分别为点A、点B，且AB=4，则图中阴影部分的面积为_____（结果保留π）．

13．化简；÷（﹣1）=______．
14．中国古代数学著作《算法统宗》中有这样一段记载：“三百七十八里关，初日健步不为难，次日脚痛减一半，六朝才得到其关．”其大意是：有人要去某关口，路程为378里，第一天健步行走，从第二天起，由于脚痛，每天走的路程都为前一天的一半，一共走了六天才到达目的地．求此人第六天走的路程为多少里．设此人第六天走的路程为x里，依题意，可列方程为________．
15．反比例函数的图象经过点（﹣3，2），则k的值是_____．当x大于0时，y随x的增大而_____．（填增大或减小）
16．八位女生的体重（单位：kg）分别为36、42、38、40、42、35、45、38，则这八位女生的体重的中位数为_____kg．
三、解答题（共8题，共72分）
17．（8分）抛物线经过A（-1，0）、C（0，-3）两点，与x轴交于另一点B．求此抛物线的解析式；已知点D 在第四象限的抛物线上，求点D关于直线BC对称的点D’的坐标;在（2）的条件下，连结BD，问在x轴上是否存在点P，使，若存在，请求出P点的坐标；若不存在，请说明理由.

18．（8分）凯里市某文具店某种型号的计算器每只进价12元，售价20元，多买优惠，优势方法是：凡是一次买10只以上的，每多买一只，所买的全部计算器每只就降价0.1元，例如：某人买18只计算器，于是每只降价0.1×（18﹣10）=0.8（元），因此所买的18只计算器都按每只19.2元的价格购买，但是每只计算器的最低售价为16元．求一次至少购买多少只计算器，才能以最低价购买？求写出该文具店一次销售x（x＞10）只时，所获利润y（元）与x（只）之间的函数关系式，并写出自变量x的取值范围；一天，甲顾客购买了46只，乙顾客购买了50只，店主发现卖46只赚的钱反而比卖50只赚的钱多，请你说明发生这一现象的原因；当10＜x≤50时，为了获得最大利润，店家一次应卖多少只？这时的售价是多少？
19．（8分）如图，在▱ABCD中，AB=4，AD=5，tanA=，点P从点A出发，沿折线AB﹣BC以每秒1个单位长度的速度向中点C运动，过点P作PQ⊥AB，交折线AD﹣DC于点Q，将线段PQ绕点P顺时针旋转90°，得到线段PR，连接QR．设△PQR与▱ABCD重叠部分图形的面积为S（平方单位），点P运动的时间为t（秒）．
（1）当点R与点B重合时，求t的值；
（2）当点P在BC边上运动时，求线段PQ的长（用含有t的代数式表示）；
（3）当点R落在▱ABCD的外部时，求S与t的函数关系式；
（4）直接写出点P运动过程中，△PCD是等腰三角形时所有的t值．

20．（8分）如图，二次函数y=ax2+2x+c的图象与x轴交于点A（﹣1，0）和点B，与y轴交于点C（0，3）．
（1）求该二次函数的表达式；
（2）过点A的直线AD∥BC且交抛物线于另一点D，求直线AD的函数表达式；
（3）在（2）的条件下，请解答下列问题：
①在x轴上是否存在一点P，使得以B、C、P为顶点的三角形与△ABD相似？若存在，求出点P的坐标；若不存在，请说明理由；
②动点M以每秒1个单位的速度沿线段AD从点A向点D运动，同时，动点N以每秒个单位的速度沿线段DB从点D向点B运动，问：在运动过程中，当运动时间t为何值时，△DMN的面积最大，并求出这个最大值．

21．（8分）如图，是5×5正方形网格，每个小正方形的边长为1，请按要求画出下列图形，所画图形的各个顶点均在所给小正方形的顶点上．

（1）在图（1）中画出一个等腰△ABE，使其面积为3.5；
（2）在图（2）中画出一个直角△CDF，使其面积为5，并直接写出DF的长．
22．（10分）如图，在△ABC中，已知AB=AC=5，BC=6，且△ABC≌△DEF，将△DEF与△ABC重合在一起，△ABC不动，△DEF运动，并满足：点E在边BC上沿B到C的方向运动，且DE始终经过点A，EF与AC交于M点．
（1）求证：△ABE∽△ECM；
（2）探究：在△DEF运动过程中，重叠部分能否构成等腰三角形？若能，求出BE的长；若不能，请说明理由；
（3）当线段AM最短时，求重叠部分的面积．

23．（12分）综合与探究：
如图，已知在△ABC 中，AB=AC，∠BAC=90°，点 A 在 x 轴上，点 B 在 y 轴上，点在二次函数的图像上．
（1）求二次函数的表达式；
（2）求点 A，B 的坐标；
（3）把△ABC 沿 x 轴正方向平移， 当点 B 落在抛物线上时， 求△ABC 扫过区域的面积．

24．小丽和哥哥小明分别从家和图书馆同时出发，沿同一条路相向而行，小丽开始跑步，遇到哥哥后改为步行，到达图书馆恰好用35分钟，小明匀速骑自行车直接回家，骑行10分钟后遇到了妹妺，再继续骑行5分钟，到家两人距离家的路程y（m）与各自离开出发的时间x（min）之间的函数图象如图所示：

（1）求两人相遇时小明离家的距离；
（2）求小丽离距离图书馆500m时所用的时间．



参考答案

一、选择题（共10小题，每小题3分，共30分）
1、C
【解析】
科学记数法的表示形式为a×10 的形式,其中1≤a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.
【详解】
0.000 000 04=4×10,
故选C
【点睛】
此题考查科学记数法，难度不大
2、D
【解析】
设直线y=x与BC交于E点，分别过A、E两点作x轴的垂线，垂足为D、F，则A（1，1），而AB=AC=2，则B（3，1），△ABC为等腰直角三角形，E为BC的中点，由中点坐标公式求E点坐标，当双曲线与△ABC有唯一交点时，这个交点分别为A、E，由此可求出k的取值范围.
解：∵，．．又∵过点，交于点，∴，
∴，∴．故选D.

3、D
【解析】
先求出一次函数的关系式，再根据函数图象与坐标轴的交点及函数图象的性质解答即可．
【详解】
由题意知，函数关系为一次函数y=-1x+4，由k=-1＜0可知，y随x的增大而减小，且当x=0时，y=4，
当y=0时，x=1．
故选D．
【点睛】
本题考查学生对计算程序及函数性质的理解．根据计算程序可知此计算程序所反映的函数关系为一次函数y=-1x+4，然后根据一次函数的图象的性质求解．
4、D
【解析】
利用二次函数的对称性，可得出图象与x轴的另一个交点坐标，结合图象可得出的解集：
由图象得：对称轴是x=2，其中一个点的坐标为（1，0），
∴图象与x轴的另一个交点坐标为（－1，0）．
由图象可知：的解集即是y＜0的解集，
∴x＜－1或x＞1．故选D．
5、D
【解析】
分析：根据主视图和俯视图之间的关系可以得出答案．
详解： ∵主视图和俯视图的长要相等， ∴只有D选项中的长和俯视图不相等，故选D．
点睛：本题主要考查的就是三视图的画法，属于基础题型．三视图的画法为：主视图和俯视图的长要相等；主视图和左视图的高要相等；左视图和俯视图的宽要相等．
6、D
【解析】
①错误．由题意a＞1．b＞1，c＜1，abc＜1；
②正确．因为y1=ax2+bx+c（a≠1）图象与直线y2=mx+n（m≠1）交于A，B两点，当ax2+bx+c＜mx+n时，-3＜x＜-1；即不等式ax2+（b-m）x+c-n＜1的解集为-3＜x＜-1；故②正确；
③错误．抛物线与x轴的另一个交点是（1，1）；
④正确．抛物线y1=ax2+bx+c（a≠1）图象与直线y=-3只有一个交点，方程ax2+bx+c+3=1有两个相等的实数根，故④正确．
【详解】
解：∵抛物线开口向上，∴a＞1，
∵抛物线交y轴于负半轴，∴c＜1，
∵对称轴在y轴左边，∴- ＜1，
∴b＞1，
∴abc＜1，故①错误．
∵y1=ax2+bx+c（a≠1）图象与直线y2=mx+n（m≠1）交于A，B两点，
当ax2+bx+c＜mx+n时，-3＜x＜-1；
即不等式ax2+（b-m）x+c-n＜1的解集为-3＜x＜-1；故②正确，
抛物线与x轴的另一个交点是（1，1），故③错误，
∵抛物线y1=ax2+bx+c（a≠1）图象与直线y=-3只有一个交点，
∴方程ax2+bx+c+3=1有两个相等的实数根，故④正确．
故选：D．
【点睛】
本题考查二次函数的性质、二次函数与不等式，二次函数与一元二次方程等知识，解题的关键是灵活运用所学知识解决问题，学会利用数形结合的思想解决问题．
7、B
【解析】
根据二次根式的性质，被开方数大于等于0，列不等式求解．
【详解】
根据题意得：x﹣1≥0，解得x≥1，
则自变量x的取值范围是x≥1．
故选B．
【点睛】
本题主要考查函数自变量的取值范围的知识点，注意：二次根式的被开方数是非负数．
8、C
【解析】
分析：根据轴对称图形与中心对称图形的概念求解．
详解：A、不是轴对称图形，也不是中心对称图形，故此选项错误；
B、是轴对称图形，也是中心对称图形，故此选项错误；
C、是轴对称图形，不是中心对称图形，故此选项正确；
D、不是轴对称图形，也不是中心对称图形，故此选项错误．
故选：C．
点睛：本题考查了中心对称图形与轴对称图形的概念：轴对称图形的关键是寻找对称轴，图形两部分沿对称轴折叠后可重合；中心对称图形是要寻找对称中心，旋转180度后与原图重合．
9、A
【解析】
由题意可知，当天最高温与最低温的温差为8-（-5）=13℃，故选A.
10、B
【解析】
在这组数据中出现次数最多的是1.1，得到这组数据的众数；把这组数据按照从小到大的顺序排列，第15、16个数的平均数是中位数．
【详解】
在这组数据中出现次数最多的是1.1，即众数是1.1．
要求一组数据的中位数，把这组数据按照从小到大的顺序排列，第15、16个两个数都是1.1，所以中位数是1.1．
故选B．
【点睛】
本题考查一组数据的中位数和众数，在求中位数时，首先要把这列数字按照从小到大或从的大到小排列，找出中间一个数字或中间两个数字的平均数即为所求．

二、填空题（本大题共6个小题，每小题3分，共18分）
11、x+1
【解析】
先通分，进行分式的加减法，再将分子进行因式分解，然后约分即可求出结果．
【详解】
解：
=


.
故答案是：x+1.
【点睛】
本题主要考查分式的混合运算，通分、因式分解和约分是解答的关键．
12、4﹣π
【解析】
由在等腰直角三角形ABC中，∠C=90°，AB=4，可求得直角边AC与BC的长，继而求得△ABC的面积，又由扇形的面积公式求得扇形EAD和扇形FBD的面积，继而求得答案．
【详解】
解：∵在等腰直角三角形ABC中，∠C=90°，AB=4，
∴AC=BC=AB•sin45°=AB=2，
∴S△ABC=AC•BC=4，
∵点D为AB的中点，
∴AD=BD=AB=2，
∴S扇形EAD=S扇形FBD=×π×22=π，
∴S阴影=S△ABC﹣S扇形EAD﹣S扇形FBD=4﹣π．
故答案为：4﹣π．
【点睛】
此题考查了等腰直角三角形的性质以及扇形的面积．注意S阴影=S△ABC﹣S扇形EAD﹣S扇形FBD．
13、-
【解析】
直接利用分式的混合运算法则即可得出.
【详解】
原式，
，
，
.
故答案为.
【点睛】
此题主要考查了分式的化简，正确掌握运算法则是解题关键.
14、;
【解析】
设第一天走了x里,则第二天走了里,第三天走了里…第六天走了里,根据总路程为378里列出方程可得答案.
【详解】
解：设第一天走了x里, 则第二天走了里,第三天走了里…第六天走了里,
依题意得:，
故答案：.
【点睛】
本题主要考查由实际问题抽象出一元一次方程.
15、﹣6 增大
【解析】
∵反比例函数的图象经过点（﹣3，2），
∴2=，即k=2×(﹣3)=﹣6，
∴k＜0，则y随x的增大而增大.
故答案为﹣6；增大.
【点睛】
本题考查用待定系数法求反函数解析式与反比例函数的性质：
（1）当k＞0时，函数图象在一，三象限，在每个象限内，y随x的增大而减小；
（2）当k＜0时，函数图象在二，四象限，在每个象限内，y随x的增大而增大.
16、1
【解析】
根据中位数的定义，结合图表信息解答即可．
【详解】
将这八位女生的体重重新排列为：35、36、38、38、40、42、42、45，
则这八位女生的体重的中位数为=1kg，
故答案为1．
【点睛】
本题考查了中位数，确定中位数的时候一定要先排好顺序，然后再根据个数是奇数或偶数来确定中位数，如果数据有奇数个，则正中间的数字即为所求，如果是偶数个则找中间两位数的平均数，中位数有时不一定是这组数据的数．

三、解答题（共8题，共72分）
17、（1）
（2）（0，-1）
（3）（1,0）（9,0）
【解析】
（1）将A（−1，0）、C（0，−3）两点坐标代入抛物线y＝ax2＋bx−3a中，列方程组求a、b的值即可；
（2）将点D（m，−m−1）代入（1）中的抛物线解析式，求m的值，再根据对称性求点D关于直线BC对称的点D'的坐标；
（3）分两种情形①过点C作CP∥BD，交x轴于P，则∠PCB＝∠CBD，②连接BD′，过点C作CP′∥BD′，交x轴于P′，分别求出直线CP和直线CP′的解析式即可解决问题．
【详解】
解：（1）将A（−1，0）、C（0，−3）代入抛物线y＝ax2＋bx−3a中，
得 ，
解得
∴y＝x2−2x−3；
（2）将点D（m，−m−1）代入y＝x2−2x−3中，得
m2−2m−3＝−m−1，
解得m＝2或−1，
∵点D（m，−m−1）在第四象限，
∴D（2，−3），
∵直线BC解析式为y＝x−3，
∴∠BCD＝∠BCO＝45°，CD′＝CD＝2，OD′＝3−2＝1，
∴点D关于直线BC对称的点D'（0，−1）；
（3）存在．满足条件的点P有两个．
①过点C作CP∥BD，交x轴于P，则∠PCB＝∠CBD，
∵直线BD解析式为y＝3x−9，
∵直线CP过点C，
∴直线CP的解析式为y＝3x−3，
∴点P坐标（1，0），
②连接BD′，过点C作CP′∥BD′，交x轴于P′，
∴∠P′CB＝∠D′BC，
根据对称性可知∠D′BC＝∠CBD，
∴∠P′CB＝∠CBD，
∵直线BD′的解析式为
∵直线CP′过点C，
∴直线CP′解析式为，
∴P′坐标为（9，0），

综上所述，满足条件的点P坐标为（1，0）或（9，0）．
【点睛】
本题考查了二次函数的综合运用．关键是由已知条件求抛物线解析式，根据抛物线的对称性，直线BC的特殊性求点的坐标，学会分类讨论，不能漏解．
18、（1）1；（3）；（3）理由见解析，店家一次应卖45只，最低售价为16.5元，此时利润最大．
【解析】
试题分析：（1）设一次购买x只，由于凡是一次买10只以上的，每多买一只，所买的全部计算器每只就降低0.10元，而最低价为每只16元，因此得到30﹣0.1（x﹣10）=16，解方程即可求解；
（3）由于根据（1）得到x≤1，又一次销售x（x＞10）只，因此得到自变量x的取值范围，然后根据已知条件可以得到y与x的函数关系式；
（3）首先把函数变为y==，然后可以得到函数的增减性，再结合已知条件即可解决问题．
试题解析：（1）设一次购买x只，则30﹣0.1（x﹣10）=16，解得：x=1．
答：一次至少买1只，才能以最低价购买；
（3）当10＜x≤1时，y=[30﹣0.1（x﹣10）﹣13]x=，当x＞1时，y=（16﹣13）x=4x；
综上所述：；
（3）y==，①当10＜x≤45时，y随x的增大而增大，即当卖的只数越多时，利润更大．
②当45＜x≤1时，y随x的增大而减小，即当卖的只数越多时，利润变小．
且当x=46时，y1=303.4，当x=1时，y3=3．∴y1＞y3．
即出现了卖46只赚的钱比卖1只赚的钱多的现象．
当x=45时，最低售价为30﹣0.1（45﹣10）=16.5（元），此时利润最大．故店家一次应卖45只，最低售价为16.5元，此时利润最大．
考点：二次函数的应用；二次函数的最值；最值问题；分段函数；分类讨论．
19、（1）；（2）（9﹣t）；（3）①S =﹣t2+t﹣；②S=﹣t2+1．③S=（9﹣t）2;（3）3或或4或．
【解析】
（1）根据题意点R与点B重合时t+t=3，即可求出t的值；
（2）根据题意运用t表示出PQ即可；
（3）当点R落在□ABCD的外部时可得出t的取值范围，再根据等量关系列出函数关系式；
（3）根据等腰三角形的性质即可得出结论.
【详解】
解：（1）∵将线段PQ绕点P顺时针旋转90°，得到线段PR，
∴PQ=PR，∠QPR=90°，
∴△QPR为等腰直角三角形．
当运动时间为t秒时，AP=t，PQ=PQ=AP•tanA=t．
∵点R与点B重合，
∴AP+PR=t+t=AB=3，
解得：t=．
（2）当点P在BC边上时，3≤t≤9，CP=9﹣t，
∵tanA=，
∴tanC=，sinC=，
∴PQ=CP•sinC=（9﹣t）．
（3）①如图1中，当＜t≤3时，重叠部分是四边形PQKB．作KM⊥AR于M．

∵△KBR∽△QAR，
∴ =，
∴ =，
∴KM=（t﹣3）=t﹣，
∴S=S△PQR﹣S△KBR=×（t）2﹣×（t﹣3）（t﹣）=﹣t2+t﹣．
②如图2中，当3＜t≤3时，重叠部分是四边形PQKB．

S=S△PQR﹣S△KBR=×3×3﹣×t×t=﹣t2+1．
③如图3中，当3＜t＜9时，重叠部分是△PQK．

S=•S△PQC=××（9﹣t）•（9﹣t）=（9﹣t）2．
（3）如图3中，

①当DC=DP1=3时，易知AP1=3，t=3．
②当DC=DP2时，CP2=2•CD•，
∴BP2=，
∴t=3+．
③当CD=CP3时，t=4．
④当CP3=DP3时，CP3=2÷，
∴t=9﹣=．
综上所述，满足条件的t的值为3或或4或．
【点睛】
本题考查四边形综合题、动点问题、平行四边形的性质、多边形的面积、等腰三角形的判定和性质等知识，解题的关键是学会用分类讨论的思想解决问题，学会利用参数构建方程解决问题，属于中考压轴题．
20、（1）y=﹣x2+2x+3；（2）y=﹣x﹣1；（3）P（）或P（﹣4.5，0）；当t=时，S△MDN的最大值为．
【解析】
（1）把A（-1，0），C（0，3）代入y=ax2+2x+c即可得到结果；
（2）在y=-x2+2x+3中，令y=0，则-x2+2x+3=0，得到B（3，0），由已知条件得直线BC的解析式为y=-x+3，由于AD∥BC，设直线AD的解析式为y=-x+b，即可得到结论；
（3）①由BC∥AD，得到∠DAB=∠CBA，全等只要当或时，△PBC∽△ABD，解方程组得D(4,−5)，求得
设P的坐标为（x，0），代入比例式解得或x=−4.5,即可得到或P(−4.5,0)；
②过点B作BF⊥AD于F，过点N作NE⊥AD于E，在Rt△AFB中，∠BAF=45°，于是得到sin∠BAF 求得求得 由于于是得到即可得到结果．
【详解】
(1)由题意知：
解得
∴二次函数的表达式为
(2)在 中,令y=0,则
解得：
∴B(3,0)，
由已知条件得直线BC的解析式为y=−x+3，
∵AD∥BC，
∴设直线AD的解析式为y=−x+b，
∴0=1+b，
∴b=−1，
∴直线AD的解析式为y=−x−1；
(3)①∵BC∥AD，
∴∠DAB=∠CBA，
∴只要当：或时,△PBC∽△ABD，
解得D(4,−5)，
∴
设P的坐标为(x,0)，
即或
解得或x=−4.5,
∴或P(−4.5,0)，
②过点B作BF⊥AD于F，过点N作NE⊥AD于E，

在Rt△AFB中,
∴sin∠BAF
∴
∴
∵
又∵
∴




∴当时,的最大值为
【点睛】
属于二次函数的综合题，考查待定系数法求二次函数解析式，锐角三角形函数，相似三角形的判定与性质，二次函数的最值等，综合性比较强，难度较大.
21、 (1)见解析；（2）DF＝
【解析】
（1）直接利用等腰三角形的定义结合勾股定理得出答案；
（2）利用直角三角的定义结合勾股定理得出符合题意的答案．
【详解】
（1）如图（1）所示：△ABE，即为所求；
（2）如图（2）所示：△CDF即为所求，DF=．

【点睛】
此题主要考查了等腰三角形的定义以及三角形面积求法，正确应用网格分析是解题关键．
22、（1）证明见解析；（2）能；BE=1或；（3）
【解析】
（1）证明：∵AB＝AC，
∴∠B＝∠C，
∵△ABC≌△DEF，
∴∠AEF＝∠B，
又∵∠AEF＋∠CEM＝∠AEC＝∠B＋∠BAE，
∴∠CEM＝∠BAE，
∴△ABE∽△ECM；
（2）能．
∵∠AEF＝∠B＝∠C，且∠AME＞∠C，
∴∠AME＞∠AEF，
∴AE≠AM；
当AE＝EM时，则△ABE≌△ECM，
∴CE＝AB＝5，
∴BE＝BC−EC＝6−5＝1，
当AM＝EM时，则∠MAE＝∠MEA，
∴∠MAE＋∠BAE＝∠MEA＋∠CEM，即∠CAB＝∠CEA，
又∵∠C＝∠C，
∴△CAE∽△CBA，
∴，
∴CE＝，
∴BE＝6−＝；
∴BE＝1或；
（3）解：设BE＝x，
又∵△ABE∽△ECM，
∴，即：，
∴CM＝，
∴AM＝5−CM，
∴当x＝3时，AM最短为，
又∵当BE＝x＝3＝BC时，
∴点E为BC的中点，
∴AE⊥BC，
∴AE＝，
此时，EF⊥AC，
∴EM＝，
S△AEM＝．
23、（1）；（2）；（3）．
【解析】
（1）将点代入二次函数解析式即可；
（2）过点作轴，证明即可得到即可得出点 A，B 的坐标；
（3）设点的坐标为，解方程得出四边形为平行四边形，求出AC，AB的值，通过扫过区域的面积=代入计算即可．
【详解】
解：(1)∵点在二次函数的图象上，
．
解方程，得
∴二次函数的表达式为．
(2)如图1，过点作轴，垂足为．


．
，

．
在和中，
∵，
．
∵点的坐标为 ，
．
．
(3)如图2，把沿轴正方向平移，

当点落在抛物线上点处时，设点的坐标为．
解方程得：(舍去)或
由平移的性质知，且，
∴四边形为平行四边形，

．
扫过区域的面积== ．
【点睛】
本题考查了二次函数与几何综合问题，涉及全等三角形的判定与性质，平行四边形的性质与判定，勾股定理解直角三角形，解题的关键是灵活运用二次函数的性质与几何的性质．
24、（1）两人相遇时小明离家的距离为1500米；（2）小丽离距离图书馆500m时所用的时间为分．
【解析】
（1）根据题意得出小明的速度，进而得出得出小明离家的距离；
（2）由（1）的结论得出小丽步行的速度，再列方程解答即可．
【详解】
解：（1）根据题意可得小明的速度为：4500÷（10+5）＝300（米/分），
300×5＝1500（米），
∴两人相遇时小明离家的距离为1500米；
（2）小丽步行的速度为：（4500﹣1500）÷（35﹣10）＝120（米/分），
设小丽离距离图书馆500m时所用的时间为x分，根据题意得，
1500+120（x﹣10）＝4500﹣500，
解得x＝．
答：小丽离距离图书馆500m时所用的时间为分．
【点睛】
本题由函数图像获取信息，以及一元一次方程的应用，由函数图像正确获取信息是解答本题的关键．