上海市徐汇区重点达标名校2022年中考数学全真模拟试卷含解析

这是一份上海市徐汇区重点达标名校2022年中考数学全真模拟试卷含解析，共20页。试卷主要包含了考生要认真填写考场号和座位序号，分式方程=1的解为，若分式有意义，则a的取值范围为等内容，欢迎下载使用。

2021-2022中考数学模拟试卷
注意事项
1．考生要认真填写考场号和座位序号。
2．试题所有答案必须填涂或书写在答题卡上，在试卷上作答无效。第一部分必须用2B 铅笔作答；第二部分必须用黑色字迹的签字笔作答。
3．考试结束后，考生须将试卷和答题卡放在桌面上，待监考员收回。

一、选择题（每小题只有一个正确答案，每小题3分，满分30分）
1．某小组在“用频率估计概率”的试验中，统计了某种结果出现的频率，绘制了如图所示的折线图，那么符合这一结果的试验最有可能的是（　　）

A．在装有1个红球和2个白球（除颜色外完全相同）的不透明袋子里随机摸出一个球是“白球”
B．从一副扑克牌中任意抽取一张，这张牌是“红色的”
C．掷一枚质地均匀的硬币，落地时结果是“正面朝上”
D．掷一个质地均匀的正六面体骰子，落地时面朝上的点数是6
2．整数a、b在数轴上对应点的位置如图，实数c在数轴上且满足，如果数轴上有一实数d，始终满足，则实数d应满足（ ）.

A． B． C． D．
3．被誉为“中国天眼”的世界上最大的单口径球面射电望远镜FAST的反射面总面积约为250000m2，则250000用科学记数法表示为( )
A．25×104m2 B．0.25×106m2 C．2.5×105m2 D．2.5×106m2
4．分式方程=1的解为（　　）
A．x=1 B．x=0 C．x=﹣ D．x=﹣1
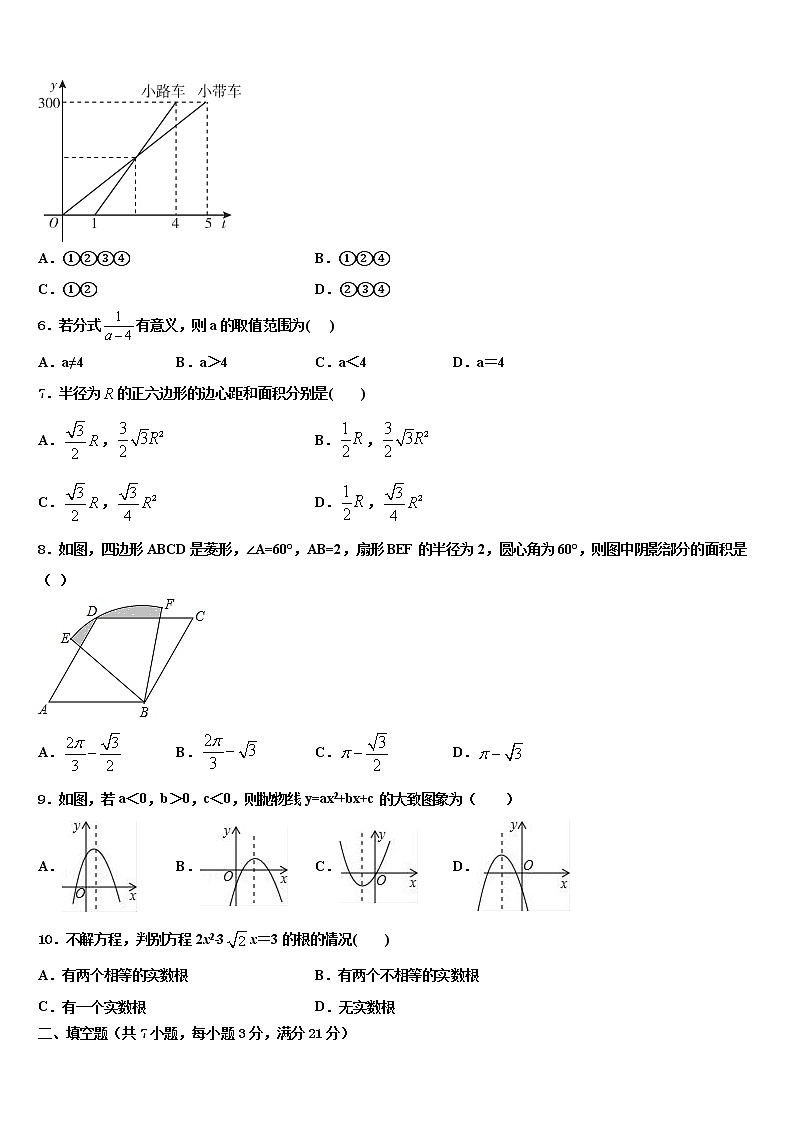
5．小带和小路两个人开车从A城出发匀速行驶至B城．在整个行驶过程中，小带和小路两人车离开A城的距离y(km)与行驶的时间t(h)之间的函数关系如图所示．有下列结论；①A，B两城相距300 km；②小路的车比小带的车晚出发1 h，却早到1 h；③小路的车出发后2.5 h追上小带的车；④当小带和小路的车相距50 km时，t＝或t＝.其中正确的结论有(　　)

A．①②③④ B．①②④
C．①② D．②③④
6．若分式有意义，则a的取值范围为( )
A．a≠4 B．a＞4 C．a＜4 D．a＝4
7．半径为的正六边形的边心距和面积分别是(　　)
A．， B．，
C．， D．，
8．如图，四边形ABCD是菱形，∠A=60°，AB=2，扇形BEF的半径为2，圆心角为60°，则图中阴影部分的面积是（ ）

A． B． C． D．
9．如图，若a＜0，b＞0，c＜0，则抛物线y=ax2+bx+c的大致图象为（　　）
A． B． C． D．
10．不解方程，判别方程2x2﹣3x＝3的根的情况(　　)
A．有两个相等的实数根 B．有两个不相等的实数根
C．有一个实数根 D．无实数根
二、填空题（共7小题，每小题3分，满分21分）
11．如果正比例函数的图像经过第一、三象限，那么的取值范围是 __．
12．在△ABC中，点D在边BC上，BD=2CD，，，那么= ．
13．从5张上面分别写着“加”“油”“向”“未”“来”这5个字的卡片（大小、形状完全相同）中随机抽取一张，则这张卡片上面恰好写着“加”字的概率是__________．
14．如图，某景区的两个景点A、B处于同一水平地面上、一架无人机在空中沿MN方向水平飞行进行航拍作业，MN与AB在同一铅直平面内，当无人机飞行至C处时、测得景点A的俯角为45°，景点B的俯角为30°，此时C到地面的距离CD为100米，则两景点A、B间的距离为__米（结果保留根号）．

15．小明把一副含45°，30°的直角三角板如图摆放，其中∠C＝∠F＝90°，∠A＝45°，∠D＝30°，则∠α+∠β等于_____．

16．如图，在正方形ABCD中，BC=2，E、F分别为射线BC，CD上两个动点，且满足BE=CF，设AE，BF交于点G，连接DG，则DG的最小值为_______．

17．请写出一个比2大且比4小的无理数：________.
三、解答题（共7小题，满分69分）
18．（10分）6月14日是“世界献血日”，某市采取自愿报名的方式组织市民义务献血．献血时要对献血者的血型进行检测，检测结果有“A型”、“B型”、“AB型”、“O型”4种类型．在献血者人群中，随机抽取了部分献血者的血型结果进行统计，并根据这个统计结果制作了两幅不完整的图表：
血型
A
B
AB
O
人数
　 　
10
5
　 　
（1）这次随机抽取的献血者人数为　 　人，m=　 　；补全上表中的数据；若这次活动中该市有3000人义务献血，请你根据抽样结果回答：
从献血者人群中任抽取一人，其血型是A型的概率是多少？并估计这3000人中大约有多少人是A型血？

19．（5分）如图，已知AB是⊙O的直径，CD与⊙O相切于C，BE∥CO．
（1）求证：BC是∠ABE的平分线；
（2）若DC=8，⊙O的半径OA=6，求CE的长．
20．（8分）在某市组织的大型商业演出活动中，对团体购买门票实行优惠，决定在原定票价基础上每张降价80元，这样按原定票价需花费6000元购买的门票张数，现在只花费了4800元．求每张门票原定的票价；根据实际情况，活动组织单位决定对于个人购票也采取优惠措施，原定票价经过连续二次降价后降为324元，求平均每次降价的百分率．
21．（10分）如图1，在直角梯形ABCD中，动点P从B点出发，沿B→C→D→A匀速运动，设点P运动的路程为x，△ABP的面积为y，图象如图2所示．
（1）在这个变化中，自变量、因变量分别是　 　、　 　；
（2）当点P运动的路程x＝4时，△ABP的面积为y＝　 　；
（3）求AB的长和梯形ABCD的面积．

22．（10分）已知C为线段上一点，关于x的两个方程与的解分别为线段的长，当时，求线段的长；若C为线段的三等分点，求m的值.
23．（12分）某中学九（1）班为了了解全班学生喜欢球类活动的情况，采取全面调查的方法，从足球、乒乓球、篮球、排球等四个方面调查了全班学生的兴趣爱好，根据调查的结果组建了4个兴趣小组，并绘制成如图所示的两幅不完整的统计图（如图①，②，要求每位学生只能选择一种自己喜欢的球类），请你根据图中提供的信息解答下列问题：

（1）九（1）班的学生人数为　 　，并把条形统计图补充完整；
（2）扇形统计图中m=　 　，n=　 　，表示“足球”的扇形的圆心角是　 　度；
（3）排球兴趣小组4名学生中有3男1女，现在打算从中随机选出2名学生参加学校的排球队，请用列表或画树状图的方法求选出的2名学生恰好是1男1女的概率．
24．（14分）如图，抛物线y=ax2+bx+c与x轴交于点A（﹣1，0），B（4，0），与y轴交于点C（0，2）
(1)求抛物线的表达式；
(2)抛物线的对称轴与x轴交于点M，点D与点C关于点M对称，试问在该抛物线的对称轴上是否存在点P，使△BMP与△ABD相似？若存在，请求出所有满足条件的P点的坐标；若不存在，请说明理由．




参考答案

一、选择题（每小题只有一个正确答案，每小题3分，满分30分）
1、D
【解析】
根据统计图可知，试验结果在0.16附近波动，即其概率P≈0.16，计算四个选项的概率，约为0.16者即为正确答案．
【详解】
根据图中信息，某种结果出现的频率约为0.16，
在装有1个红球和2个白球（除颜色外完全相同）的不透明袋子里随机摸出一个球是“白球”的概率为≈0.67>0.16，故A选项不符合题意，
从一副扑克牌中任意抽取一张，这张牌是“红色的”概率为≈0.48>0.16，故B选项不符合题意，
掷一枚质地均匀的硬币，落地时结果是“正面朝上”的概率是=0.5>0.16，故C选项不符合题意，
掷一个质地均匀的正六面体骰子，落地时面朝上的点数是6的概率是≈0.16，故D选项符合题意，
故选D.
【点睛】
本题考查了利用频率估计概率，大量反复试验下频率稳定值即概率．用到的知识点为：频率=所求情况数与总情况数之比．熟练掌握概率公式是解题关键.
2、D
【解析】
根据a≤c≤b，可得c的最小值是﹣1，根据有理数的加法，可得答案．
【详解】
由a≤c≤b，得：c最小值是﹣1，当c=﹣1时，c+d=﹣1+d，﹣1+d≥0，解得：d≥1，∴d≥b．
故选D．
【点睛】
本题考查了实数与数轴，利用a≤c≤b得出c的最小值是﹣1是解题的关键．
3、C
【解析】
科学记数法的表示形式为a×10n，其中1≤|a|＜10，n为整数．
【详解】
解：由科学记数法可知：250000 m2=2.5×105m2，
故选C．
【点睛】
此题考查科学记数法表示较大的数的方法，准确确定a与n值是关键．
4、C
【解析】
首先找出分式的最简公分母，进而去分母，再解分式方程即可．
【详解】
解：去分母得：
x2-x-1=（x+1）2，
整理得：-3x-2=0，
解得：x=-，
检验：当x=-时，（x+1）2≠0，
故x=-是原方程的根．
故选C．
【点睛】
此题主要考查了解分式方程的解法，正确掌握解题方法是解题关键．
5、C
【解析】
观察图象可判断①②，由图象所给数据可求得小带、小路两车离开A城的距离y与时间t的关系式，可求得两函数图象的交点，可判断③，再令两函数解析式的差为50，可求得t，可判断④，可得出答案．
【详解】
由图象可知A，B两城市之间的距离为300 km，小带行驶的时间为5 h，而小路是在小带出发1 h后出发的，且用时3 h，即比小带早到1 h，
∴①②都正确；
设小带车离开A城的距离y与t的关系式为y小带＝kt，
把(5，300)代入可求得k＝60，
∴y小带＝60t，
设小路车离开A城的距离y与t的关系式为y小路＝mt＋n，
把(1，0)和(4，300)代入可得
解得
∴y小路＝100t－100，
令y小带＝y小路，可得60t＝100t－100，
解得t＝2.5，
即小带和小路两直线的交点横坐标为t＝2.5，
此时小路出发时间为1.5 h，即小路车出发1.5 h后追上甲车，
∴③不正确；
令|y小带－y小路|＝50，
可得|60t－100t＋100|＝50，即|100－40t|＝50，
当100－40t＝50时，
可解得t＝，
当100－40t＝－50时，
可解得t＝，
又当t＝时，y小带＝50，此时小路还没出发，
当t＝时，小路到达B城，y小带＝250.
综上可知当t的值为或或或时，两车相距50 km，
∴④不正确．
故选C.
【点睛】
本题主要考查一次函数的应用，掌握一次函数图象的意义是解题的关键，特别注意t是甲车所用的时间．
6、A
【解析】
分式有意义时，分母a-4≠0
【详解】
依题意得：a−4≠0，
解得a≠4.
故选：A
【点睛】
此题考查分式有意义的条件，难度不大
7、A
【解析】
首先根据题意画出图形，易得△OBC是等边三角形，继而可得正六边形的边长为R，然后利用解直角三角形求得边心距，又由S正六边形=求得正六边形的面积．
【详解】
解：如图，O为正六边形外接圆的圆心，连接OB，OC，过点O作OH⊥BC于H，

∵六边形ABCDEF是正六边形，半径为，
∴∠BOC=，
∵OB=OC=R，
∴△OBC是等边三角形，
∴BC=OB=OC=R，
∵OH⊥BC，
∴在中，，
即，
∴，即边心距为；
∵，
∴S正六边形=，
故选：A．
【点睛】
本题考查了正多边形和圆的知识；求得正六边形的中心角为60°，得到等边三角形是正确解答本题的关键．
8、B
【解析】
根据菱形的性质得出△DAB是等边三角形，进而利用全等三角形的判定得出△ABG≌△DBH，得出四边形GBHD的面积等于△ABD的面积，进而求出即可．
【详解】
连接BD，

∵四边形ABCD是菱形，∠A=60°，
∴∠ADC=120°，
∴∠1=∠2=60°，
∴△DAB是等边三角形，
∵AB=2，
∴△ABD的高为，
∵扇形BEF的半径为2，圆心角为60°，
∴∠4+∠5=60°，∠3+∠5=60°，
∴∠3=∠4，
设AD、BE相交于点G，设BF、DC相交于点H，
在△ABG和△DBH中，
，
∴△ABG≌△DBH（ASA），
∴四边形GBHD的面积等于△ABD的面积，
∴图中阴影部分的面积是：S扇形EBF-S△ABD=
=．
故选B．
9、B
【解析】
由抛物线的开口方向判断a的符号，由抛物线与y轴的交点判断c的符号，然后根据对称轴及抛物线与x轴交点情况进行推理，进而对所得结论进行判断．
【详解】
∵a＜0，
∴抛物线的开口方向向下，
故第三个选项错误；
∵c＜0，
∴抛物线与y轴的交点为在y轴的负半轴上，
故第一个选项错误；
∵a＜0、b＞0，对称轴为x=＞0，
∴对称轴在y轴右侧，
故第四个选项错误．
故选B．
10、B
【解析】
一元二次方程的根的情况与根的判别式有关，
，方程有两个不相等的实数根，故选B

二、填空题（共7小题，每小题3分，满分21分）
11、k>1
【解析】
根据正比例函数y=（k-1）x的图象经过第一、三象限得出k的取值范围即可．
【详解】
因为正比例函数y=（k-1）x的图象经过第一、三象限，
所以k-1＞0，
解得：k＞1，
故答案为：k＞1．
【点睛】
此题考查一次函数问题，关键是根据正比例函数y=（k-1）x的图象经过第一、三象限解答．
12、
【解析】
首先利用平行四边形法则，求得的值，再由BD=2CD，求得的值，即可求得的值．
【详解】
∵，，
∴=-=-，
∵BD=2CD，
∴==，
∴=+==．

故答案为．
13、
【解析】
根据概率的公式进行计算即可.
【详解】
从5张上面分别写着“加”“油”“向”“未”“来”这5个字的卡片中随机抽取一张，则这张卡片上面恰好写着“加”字的概率是.
故答案为：.
【点睛】
考查概率的计算，明确概率的意义是解题的关键，概率等于所求情况数与总情况数的比.
14、100+100
【解析】
【分析】由已知可得∠ACD=∠MCA=45°，∠B=∠NCB=30°，继而可得∠DCB=60°，从而可得AD=CD=100米，DB= 100米，再根据AB=AD+DB计算即可得.
【详解】∵MN//AB，∠MCA=45°，∠NCB=30°，
∴∠ACD=∠MCA=45°，∠B=∠NCB=30°，
∵CD⊥AB，∴∠CDA=∠CDB=90°，∠DCB=60°，
∵CD=100米，∴AD=CD=100米，DB=CD•tan60°=CD=100米，
∴AB=AD+DB=100+100（米），
故答案为：100+100．
【点睛】本题考查了解直角三角形的应用﹣﹣仰角俯角问题，解题的关键是借助俯角构造直角三角形并解直角三角形．注意方程思想与数形结合思想的应用．
15、210°
【解析】
根据三角形内角和定理得到∠B＝45°，∠E＝60°，根据三角形的外角的性质计算即可．
【详解】
解：如图：

∵∠C＝∠F＝90°，∠A＝45°，∠D＝30°，
∴∠B＝45°，∠E＝60°，
∴∠2+∠3＝120°，
∴∠α+∠β＝∠A+∠1+∠4+∠B＝∠A+∠B+∠2+∠3＝90°+120°＝210°，
故答案为：210°．
【点睛】
本题考查的是三角形的外角的性质、三角形内角和定理，掌握三角形的一个外角等于和它不相邻的两个内角的和是解题的关键．
16、﹣1
【解析】
先由图形确定：当O、G、D共线时，DG最小；根据正方形的性质证明△ABE≌△BCF（SAS），可得∠AGB=90°，利用勾股定理可得OD的长，从而得DG的最小值．
【详解】

在正方形ABCD中，AB=BC，∠ABC=∠BCD，
在△ABE和△BCF中，
，
∴△ABE≌△BCF(SAS)，
∴∠BAE=∠CBF，
∵∠CBF+∠ABF=90°
∴∠BAE+∠ABF=90°
∴∠AGB=90°
∴点G在以AB为直径的圆上，
由图形可知：当O、G、D在同一直线上时，DG有最小值，如图所示：
∵正方形ABCD，BC=2，
∴AO=1=OG
∴OD=，
∴DG=−1，
故答案为−1.
【点睛】
本题考查了正方形的性质与全等三角形的判定与性质，解题的关键是熟练的掌握正方形的性质与全等三角形的判定与性质.
17、（或）
【解析】
利用完全平方数和算术平方根对无理数的大小进行估算，然后找出无理数即可
【详解】
设无理数为，，所以x的取值在4~16之间都可，故可填
【点睛】
本题考查估算无理数的大小，能够判断出中间数的取值范围是解题关键

三、解答题（共7小题，满分69分）
18、（1）50，20；（2）12，23；见图；（3）大约有720人是A型血．
【解析】
【分析】（1）用AB型的人数除以它所占的百分比得到随机抽取的献血者的总人数，然后用B型的人数除以抽取的总人数即可求得m的值；
（2）先计算出O型的人数，再计算出A型人数，从而可补全上表中的数据；
（3）用样本中A型的人数除以50得到血型是A型的概率，然后用3000乘以此概率可估计这3000人中是A型血的人数．
【详解】（1）这次随机抽取的献血者人数为5÷10%=50（人），
所以m=×100=20，
故答案为50，20；
（2）O型献血的人数为46%×50=23（人），
A型献血的人数为50﹣10﹣5﹣23=12（人），
补全表格中的数据如下：
血型
A
B
AB
O
人数
12
10
5
23
故答案为12，23；
（3）从献血者人群中任抽取一人，其血型是A型的概率=，
3000×=720，
估计这3000人中大约有720人是A型血．
【点睛】本题考查了扇形统计图、统计表、概率公式、用样本估计总体等，读懂统计图、统计表，从中找到必要的信息是解题的关键；随机事件A的概率P（A）=事件A可能出现的结果数除以所有可能出现的结果数．
19、（1）证明见解析；（2）4.1．
【解析】
试题分析：（1）由BE∥CO，推出∠OCB=∠CBE，由OC=OB，推出∠OCB=∠OBC，可得∠CBE=∠CBO；
（2）在Rt△CDO中，求出OD，由OC∥BE，可得，由此即可解决问题；
试题解析：（1）证明：∵DE是切线，∴OC⊥DE，∵BE∥CO，∴∠OCB=∠CBE，∵OC=OB，∴∠OCB=∠OBC，∴∠CBE=∠CBO，∴BC平分∠ABE．
（2）在Rt△CDO中，∵DC=1，OC=0A=6，∴OD==10，∵OC∥BE，∴，∴，∴EC=4.1．
考点：切线的性质．
20、（1）1（2）10%．
【解析】
试题分析：（1）设每张门票的原定票价为x元，则现在每张门票的票价为（x-80）元，根据“按原定票价需花费6000元购买的门票张数，现在只花费了4800元”建立方程，解方程即可；
（2）设平均每次降价的百分率为y，根据“原定票价经过连续二次降价后降为324元”建立方程，解方程即可．
试题解析：（1）设每张门票的原定票价为x元，则现在每张门票的票价为（x-80）元，根据题意得
，
解得x=1．
经检验，x=1是原方程的根．
答：每张门票的原定票价为1元；
（2）设平均每次降价的百分率为y，根据题意得
1（1-y）2=324，
解得：y1=0.1，y2=1.9（不合题意，舍去）．
答：平均每次降价10%．
考点：1.一元二次方程的应用；2.分式方程的应用．
21、（1）x，y；（2）2；（3）AB=8，梯形ABCD的面积=1．
【解析】
（1）依据点P运动的路程为x，△ABP的面积为y，即可得到自变量和因变量；
（2）依据函数图象，即可得到点P运动的路程x=4时，△ABP的面积；
（3）根据图象得出BC的长，以及此时三角形ABP面积，利用三角形面积公式求出AB的长即可；由函数图象得出DC的长，利用梯形面积公式求出梯形ABCD面积即可．
【详解】
（1）∵点P运动的路程为x，△ABP的面积为y，∴自变量为x，因变量为y．
故答案为x，y；
（2）由图可得：当点P运动的路程x=4时，△ABP的面积为y=2．
故答案为2；
（3）根据图象得：BC=4，此时△ABP为2，∴AB•BC=2，即×AB×4=2，解得：AB=8；
由图象得：DC=9﹣4=5，则S梯形ABCD=×BC×（DC+AB）=×4×（5+8）=1．
【点睛】
本题考查了动点问题的函数图象，弄清函数图象上的信息是解答本题的关键．
22、（1）；（2）或1.
【解析】
（1）把m=2代入两个方程，解方程即可求出AC、BC的长，由C为线段上一点即可得AB的长；（2）分别解两个方程可得，，根据为线段的三等分点分别讨论为线段靠近点的三等分点和为线段靠近点的三等分点两种情况，列关于m的方程即可求出m的值.
【详解】
（1）当时，有，，
由方程，解得，即.
由方程，解得，即.
因为为线段上一点，
所以.
（2）解方程，得，
即.
解方程，得，
即.
①当为线段靠近点的三等分点时，
则，即，解得.
②当为线段靠近点的三等分点时，
则，即，解得.
综上可得，或1.
【点睛】
本题考查一元一次方程的几何应用，注意讨论C点的位置，避免漏解是解题关键.
23、（1）4，补全统计图见详解.（2）10；20；72.（3）见详解.
【解析】
（1）根据喜欢篮球的人数与所占的百分比列式计算即可求出学生的总人数，再求出喜欢足球的人数，然后补全统计图即可；
（2）分别求出喜欢排球、喜欢足球的百分比即可得到m、n的值，用喜欢足球的人数所占的百分比乘以360°即可；
（3）画出树状图，然后根据概率公式列式计算即可得解．
【详解】
解： (1)九(1)班的学生人数为：12÷30%=40(人)，
喜欢足球的人数为：40−4−12−16=40−32=8(人)，
补全统计图如图所示；

(2)∵×100%=10%，
×100%=20%，
∴m=10，n=20，
表示“足球”的扇形的圆心角是20%×360°=72°；
故答案为(1)40;(2)10；20；72；
(3)根据题意画出树状图如下：

一共有12种情况，恰好是1男1女的情况有6种，
∴P(恰好是1男1女)==.
24、 (1)y=﹣x2+x+2；(2)满足条件的点P的坐标为（，）或（，﹣）或（，5）或（，﹣5）．
【解析】
（1）利用待定系数法求抛物线的表达式；
（2）使△BMP与△ABD相似的有三种情况，分别求出这三个点的坐标.
【详解】
(1)∵抛物线与x轴交于点A（﹣1，0），B（4，0），
∴设抛物线的解析式为y=a（x+1）（x﹣4），
∵抛物线与y轴交于点C（0，2），
∴a×1×（﹣4）=2，
∴a=﹣，
∴抛物线的解析式为y=﹣（x+1）（x﹣4）=﹣x2+x+2；
(2)如图1，连接CD，∵抛物线的解析式为y=﹣x2+x+2，
∴抛物线的对称轴为直线x=，
∴M（，0），∵点D与点C关于点M对称，且C（0，2），
∴D（3，﹣2），
∵MA=MB，MC=MD，
∴四边形ACBD是平行四边形，
∵A（﹣1，0），B（4，0），C（3，﹣22），
∴AB2=25，BD2=（4﹣1）2+22=5，AD2=（3+1）2+22=20，
∴AD2+BD2=AB2，
∴△ABD是直角三角形，
∴∠ADB=90°，
设点P（，m），
∴MP=|m|，
∵M（，0），B（4，0），
∴BM=，
∵△BMP与△ABD相似，
∴①当△BMP∽ADB时，
∴，
∴，
∴m=±，
∴P（，）或（，﹣），
②当△BMP∽△BDA时，
，
∴，
∴m=±5，
∴P（，5）或（，﹣5），
即：满足条件的点P的坐标为P（，）或（，﹣）或（，5）或（，﹣5）．
【点睛】
本题考查了二次函数的应用，解题的关键是熟练的掌握二次函数的应用.