






初中数学人教版九年级上册24.2.2 直线和圆的位置关系教学课件ppt
展开1.理解直线和圆的三种位置关系时圆心到直线的距离d和圆的半径r之间的数量关系. (难点)2.会运用直线和圆的三种位置关系的性质与判定进行有关计算. (重点)
定理:过不在同一直线上的三个点确定一个圆
一个三角形的外接圆是唯一的
反证法的证明思想:反设、归谬、结论
如果我们把太阳看成一个圆,地平线看成一条直线,那你能根据直线和圆的公共点个数想象一下,直线和圆有几种位置关系吗?
知识点1 直线与圆的位置关系的判定
如图,在纸上画一条直线 l,把钥匙环看作一个圆.在纸上移动钥匙环,你能发现在移动钥匙环的过程中,它与直线 l 的公共点个数的变化情况吗?
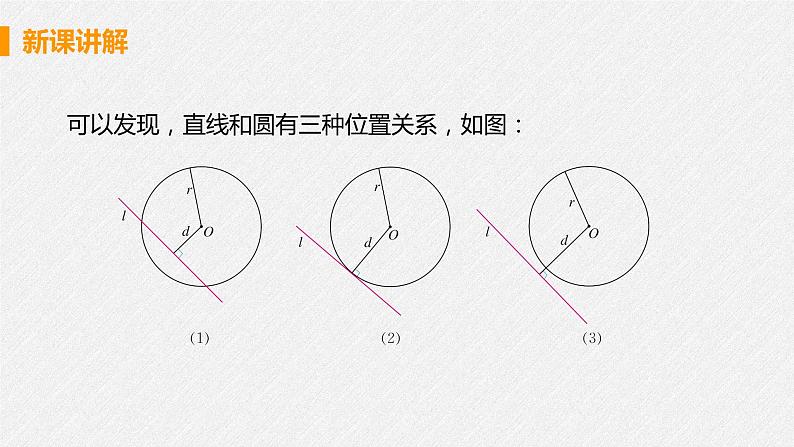
可以发现,直线和圆有三种位置关系,如图:
如图(1),直线和圆有两个公共点,这时我们说这条直线和圆相交,这条直线叫做圆的割线.
如图(2),直线和圆只有一个公共点,这时我们说这条直线和圆相切,这条直线叫做圆的切线,这个点叫做切点.
如图(3),直线和圆没有公共点,这时我们说这条直线和圆相离.
怎样用d (圆心与直线的距离)来判别直线与圆的位置关系呢?
用圆心O到直线的距离d与圆的半径r的关系来区分直线与圆的位置关系:
1.判断直线和圆的位置关系有两种方法: ①将圆心到直线的距离与圆的半径相比较; ②根据直线与圆的交点的个数判定.
2.直线与圆相切是一种特殊的位置关系,此时直线与圆只有一个交点.一个圆有无数条切线,每一条切线与圆都只有一个切点.
1 已知圆的直径为13 cm,设直线和圆心的距离为d.(1) 若d =4.5 cm,则直线与圆 ,直线与圆有 个公共点;(2) 若d =6.5 cm,则直线与圆 ,直线与圆有 个公共点;(3) 若d = 8 cm,则直线与圆 ,直线与圆有 个公共点.
1. 已知⊙O的半径为5 cm,圆心O到直线 l 的距离为5cm,则直线 l 与⊙O的位置关系为( )
A.相交B.相切C.相离D.无法确定
2. 如图,Rt△ABC中,∠C=90°,AC=3 cm,BC=4 cm,判断以点C为圆心,下列 r 为半径的⊙C与AB的位置关系:(1) r =2 cm; (2) r=2.4 cm; (3) r =3 cm.
相离:d>r相切:d=r相交:d
d>r:相离d=r:相切d
1.已知⊙O的半径是6,点O到直线l的距离为5,则直线l与⊙O的位置关系是( )A.相离 B.相切 C.相交 D.无法判断2.直线l与半径为r的⊙O相离,且点O到直线l的距离为6,则r的取值范围是( )A.r<6 B.r=6 C.r>6 D.r≥6
3.⊙O的半径为4cm,圆心O到直线l的距离为4cm,则直线l与⊙O的位置关系为 . 4.如图,在Rt△ABC中,∠C=90°,∠A=60°,BC=4cm,以点C为圆心,3cm长为半径作圆,则⊙C与AB的位置关系是 .
如图,在平面直角坐标系中有一矩形OABC,点B的坐标为(4,2),现有一圆同时和这个矩形的三边都相切,则此圆的圆心D的坐标为 .分析:若与OA,AB,BC三条边相切,D的坐标为(3,1);若与OA,BC,CO三条边相切,D的坐标为(1,1);若与OA,AB,CO三条边相切,D的坐标为(2,2);若与AB,BC,CO三条边相切,D的坐标为(2,0).
(1,1),(3,1)(2,2)和(2,0)
初中数学人教版九年级上册第二十四章 圆24.2 点和圆、直线和圆的位置关系24.2.2 直线和圆的位置关系评课ppt课件: 这是一份初中数学人教版九年级上册第二十四章 圆24.2 点和圆、直线和圆的位置关系24.2.2 直线和圆的位置关系评课ppt课件
人教版九年级上册24.2.2 直线和圆的位置关系课文配套课件ppt: 这是一份人教版九年级上册24.2.2 直线和圆的位置关系课文配套课件ppt,共22页。PPT课件主要包含了●学习目标,针对训练,BC⊥AB等内容,欢迎下载使用。
九年级上册24.2.2 直线和圆的位置关系图片课件ppt: 这是一份九年级上册24.2.2 直线和圆的位置关系图片课件ppt,共18页。PPT课件主要包含了CONTENTS,切线长,切线长定理,巩固应用等内容,欢迎下载使用。













