2020-2021学年22.3 实际问题与二次函数教案配套ppt课件

这是一份2020-2021学年22.3 实际问题与二次函数教案配套ppt课件，共17页。PPT课件主要包含了学习目标，新课导入，新课讲解，课堂小结，当堂小练，拓展与延伸，布置作业，几何面积最值问题，一个关键，一个注意等内容，欢迎下载使用。

1.能够从实际问题中抽象出二次函数关系. （难点） 2.会运用二次函数求实际问题中的最大值或最小值. 3.能应用二次函数的性质解决图形中最大面积问题. （重点）
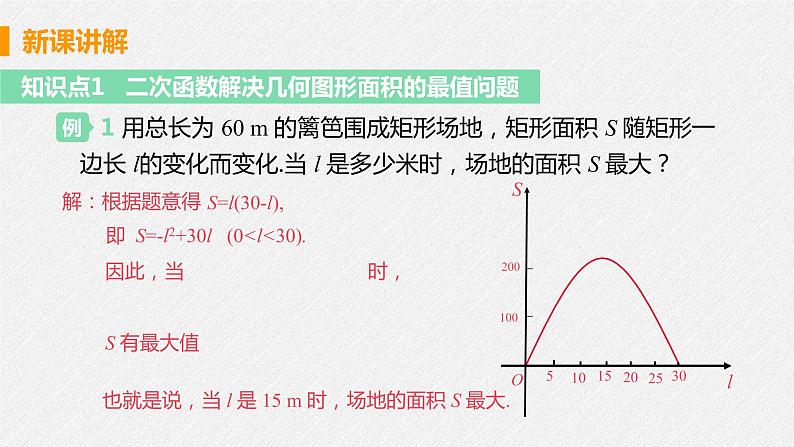
用总长为60m的篱笆围成矩形场地，矩形面积S随矩形一边长l的变化而变化.当l是多少米时，场地的面积S最大？
写出下列抛物线的开口方向、对称轴和顶点坐标，并写出其最值.（1）y= x2-2x-3；（公式法）（2）y=-x2-3x+4.（配方法）
知识点1 二次函数解决几何图形面积的最值问题
1 用总长为 60 m 的篱笆围成矩形场地，矩形面积 S 随矩形一边长 l的变化而变化.当 l 是多少米时，场地的面积 S 最大？
即 S=-l2+30l (0也就是说，当 l 是 15 m 时，场地的面积 S 最大.
2 变式，如图，用一段长为60 m的篱笆围成一个一边靠墙的矩形菜园，墙长18 m，这个矩形的长、宽各为多少时，菜园的面积最大？最大面积是多少?
解：根据题意设矩形菜园平行于墙的一边长为l m，菜园的面积为S m2 ，
但因为0原本当 l=30 时，S取得最大值，
当 l<30 时，S 随 l 的增大而增大，当 l>30 时，S 随 l 的增大而减小，
注意 实际问题中求解二次函数最值问题时，函数的最值要考虑自变量的取值范围：（1）当自变量的取值包含顶点时，函数的最值在函数的顶点处取得；（2）当自变量的取值不包含顶点时，函数的最值一般在端点处取得，此时要考虑函数的增减性.
用二次函数解决实际问题的一般步骤：
1.审：仔细审题，厘清题意；2.设：找出题中的变量和常量，分析它们之间的关系，与图形相关的问题要结合图形具体分析，设出适当的未知数；3.列：用二次函数表示出变量和常量之间的关系，建立二次函数模型，写出二次函数的解析式；4.解：依据已知条件，借助二次函数的解析式、图象和性质等求解实际问题；5.检：检验结果，进行合理取舍，得出符合实际意义的结论.
二次函数解决几何面积最值问题的方法
1.求出函数解析式和自变量的取值范围；2.配方变形，或利用公式求它的最大值或最小值,3.检查求得的最大值或最小值对应的自变量的值是否在自变量的取值范围内.
在美化校园的活动中，某兴趣小组想借助如图所示的直角墙角(两边足够长)，用 28 m 长的篱笆围成一个矩形花园 ABCD (篱笆只围 AB，BC 两边)，设 AB=x m，花园面积为 S m2.(1)求 S 与 x 之间的函数关系式；(2)当 x 为何值时，S 有最大值？请求出最大值.
解：(1)由题意得 AD=(28-x) m，则 S=x(28-x)=-x2+28x(0常见几何图形的面积公式
最值有时不在顶点处，则要利用函数的增减性来确定
1.如图，四边形的两条对角线AC、BD互相垂直，AC+BD=10，当AC、BD的长是多少时，四边形ABCD的面积最大？
解：设AC=x,四边形ABCD面积为y,则BD=(10-x).即当AC、BD的长均为5时，四边形ABCD的面积最大.
2.如图，点E、F、G、H分别位于正方形ABCD的四条边上，四边形EFGH也是正方形，当点E位于何处时，正方形EFGH的面积最小？
解：令AB长为1，设DH=x，正方形EFGH的面积为y，则DG=1-x.即当E位于AB中点时，正方形EFGH面积最小.
已知矩形的周长为36 cm，矩形绕它的一条边旋转形成一个圆柱，矩形的长、宽各为多少时，圆柱的侧面积最大？
解：设矩形的长为xcm，圆柱的侧面积为ycm2，则矩形的宽为(18-x)cm，绕矩形的长或宽旋转，圆柱的侧面积相等.有y=2πx(18-x)＝-2π(x-9)2+162π(0＜x＜18).当x=9时，y有最大值为162π.即当矩形的长、宽各为9cm时，圆柱的侧面积最大。