专题04 二次函数系数之间的关系-备战2023年中考数学压轴题满分突破之二次函数篇（无答案）

这是一份专题04 二次函数系数之间的关系-备战2023年中考数学压轴题满分突破之二次函数篇（无答案），共7页。试卷主要包含了二次函数各系数之间的关系等内容，欢迎下载使用。
第四讲 二次函数系数之间的关系目录必备知识点考点一 二次函数各系数之间的关系  必备知识点知识点1  二次函数图像和系数的关系
1.二次项系数a决定抛物线的开口方向和大小．
当a＞0时，抛物线向上开口；当a＜0时，抛物线向下开口；IaI还可以决定开口大小，IaI越大开口就越小．
2.一次项系数b和二次项系数a共同决定对称轴的位置．
当a与b同号时（即ab＞0），对称轴在y轴左； 当a与b异号时（即ab＜0），对称轴在y轴右．（简称：左同右异）
3.常数项c决定抛物线与y轴交点． 抛物线与y轴交于（0，c）．
4.抛物线与x轴交点个数．
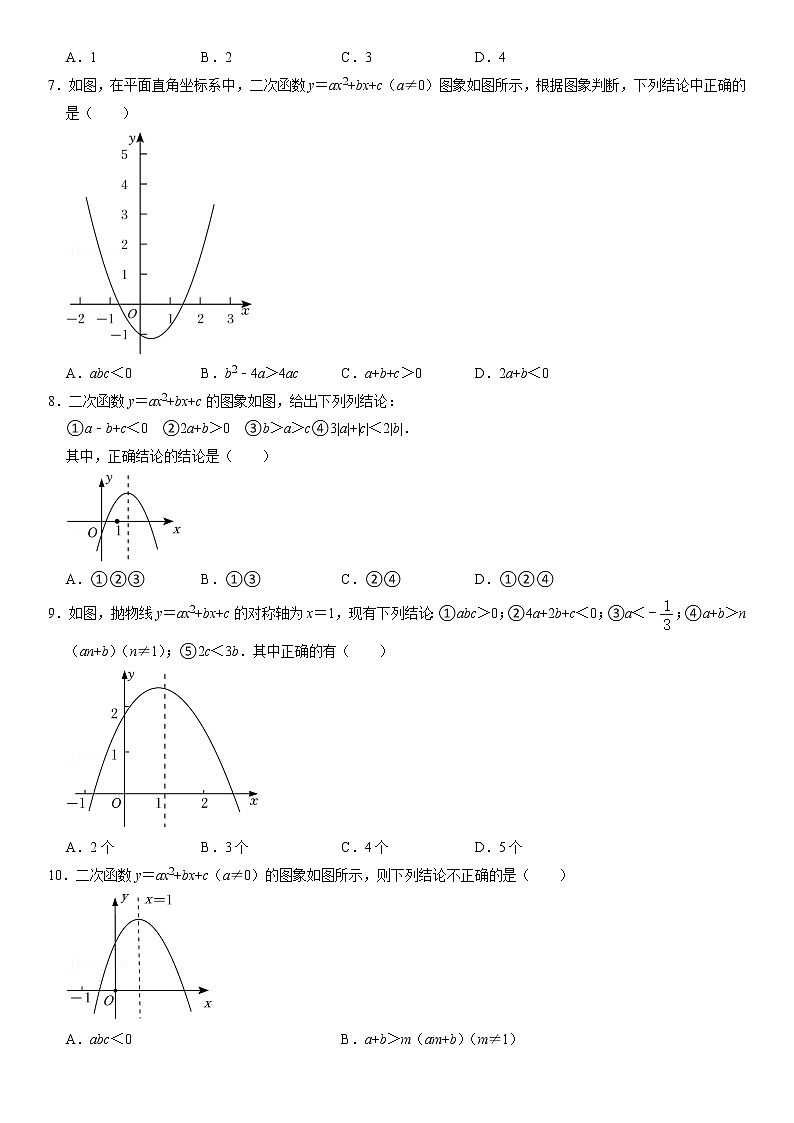
（1）△=b2-4ac＞0时，抛物线与x轴有2个交点（2）△=b2-4ac=0时，抛物线与x轴有1个交点（3）△=b2-4ac＜0时，抛物线与x轴没有交点  考点一 二次函数各系数之间的关系 1．在平面直角坐标系中，已知二次函数y＝ax2+bx+c（a≠0）的图象如图所示，有下列5个结论：①abc＞0；②2a﹣b＝0；③9a+3b+c＞0；④b2＞4ac；⑤a+c＜b．其中正确的有（　　）A．1个 B．2个 C．3个 D．4个2．二次函数y＝ax2+bx+c（a≠0）的图象如图所示，现有下列结论：①abc＞0；②3a+c＝0；③4a﹣2b+c＜0；④a+b＞m（am+b）其中m是不等于1的实数．则其中结论正确的个数是多少个（　　）A．1 B．2 C．3 D．43．二次函数y＝ax2+bx+c（a≠0）的图象如图所示，有下列结论：①abc＞0；②2c＜3b；③a+2b＞m（am+b）（m≠1）；④若方程|ax2+bx+c|＝1有四个根，则这四个根的和为2．其中，正确结论的个数是（　　）A．1 B．2 C．3 D．44．二次函数y＝ax2+bx+c（a≠0）的图象如图所示，已知其对称轴为x＝1，则下列结论正确的是（　　）A．abc＜0 B．2a﹣b＝0 C．5a+3b+2c＜0 D．4ac﹣b2＞05．如图，抛物线y＝ax2+bx+c与x轴相交于点A（﹣2，0）、B（6，0），与y轴相交于点C，小红同学得出了以下结论：①b2﹣4ac＞0；②4a+b＝0；③当y＞0时，﹣2＜x＜6；④a+b+c＜0．其中正确的个数为（　　）A．4 B．3 C．2 D．16．已知二次函数y＝ax2+bx+c（a≠0）的图象如图所示，其顶点为（，1），有下列结论：①ac＜0；②函数最大值为1；③b2﹣4ac＜0；④2a+b＝0．其中，正确结论的个数是（　　）A．1 B．2 C．3 D．47．如图，在平面直角坐标系中，二次函数y＝ax2+bx+c（a≠0）图象如图所示，根据图象判断，下列结论中正确的是（　　）A．abc＜0 B．b2﹣4a＞4ac C．a+b+c＞0 D．2a+b＜08．二次函数y＝ax2+bx+c的图象如图，给出下列列结论：①a﹣b+c＜0  ②2a+b＞0  ③b＞a＞c④3|a|+|c|＜2|b|．其中，正确结论的结论是（　　）A．①②③ B．①③ C．②④ D．①②④9．如图，抛物线y＝ax2+bx+c的对称轴为x＝1，现有下列结论：①abc＞0；②4a+2b+c＜0；③a＜﹣；④a+b＞n（an+b）（n≠1）；⑤2c＜3b．其中正确的有（　　）A．2个 B．3个 C．4个 D．5个10．二次函数y＝ax2+bx+c（a≠0）的图象如图所示，则下列结论不正确的是（　　）A．abc＜0 B．a+b＞m（am+b）（m≠1） C．4a﹣2b+c＜0 D．3a+c＝111．二次函数y＝ax2+bx+c的图象如图所示，其对称轴为x＝﹣1，有下列结论：①abc＞0；②a+b＜﹣c；③4a﹣2b+c＞0；④3b+2c＜0；⑤a﹣b＜m（am+b）（其中m为任意实数），其中正确结论的个数有（　　）A．2个 B．3个 C．4个 D．5个12．二次函数y＝ax2+bx+c（a≠0）的图象如图所示．下列结论：①abc＞0；②a﹣b+c＞0；③m为任意实数，则a+b＞am2+bm；④3a+c＜0；⑤若ax12+bx1＝ax22+bx2且x1≠x2，则x1+x2＝2．其中正确结论的个数有（　　）A．1个 B．2个 C．3个 D．4个13．二次函数y＝ax2+bx+c的图象如图所示，对称轴是直线x＝1，下列结论：①abc＞0；②2a+b＜0；③a﹣b+c＞0；④9a+3b+c＜0．其中正确的是（　　）A．①③④ B．①②③ C．①③ D．②③14．二次函数y＝ax2+bx+c（a≠0）的图象如图所示，下列结论：①abc＞0；②b2＞4ac；③a﹣b+c＜0；④a+c＜1；正确的个数是（　　）A．1个 B．2个 C．3个 D．4个15．如图，抛物线y＝ax2+bx+c的对称轴为x＝1，现有下列结论：①abc＞0；②a＜﹣；③4a+2b+c＜0；④a+b＞n（an+b）（n≠1）；⑤2c＜3b．正确的个数是（　　）A．2个 B．3个 C．4个 D．5个16．如图，已知二次函数y＝ax2+bx+c给出下列结论：①abc＜0，②4a+2b+c＜0，③a+c＞b，④a+b≤t（at+b）（t是任意一个实数），⑤当x＜﹣1时，y随x的增大而减少．其中结论正确的个数是（　　）A．2个 B．3个 C．4个 D．5个17．已知抛物线y＝ax2+bx+c（a、b、c是常数，a＜0）经过点（﹣2，0），其对称轴为直线x＝1，有下列结论：①c＞0；②9a+3b+c＞0；③若方程ax2+bx+c+1＝0有解x1、x2，满足x1＜x2，则x1＜﹣2，x2＞4；④抛物线与直线y＝x交于P、Q两点，若PQ＝，则a＝﹣1；其中，正确结论的个数是（　　）个．A．4 B．3 C．2 D．118．二次函数y＝ax2+bx+c的图象如图所示，给出下列说法：①abc＜0；②方程ax2+bx+c＝0的根为x1＝﹣1、x2＝3；③若直线y＝2与y＝ax2+bx+c的图象相交于A（x3，y1），B（x4，y2），（x3＜x4）两点则x1、x2、x3、x4的大小关系是x1＜x2＜x3＜x4；④当y＞0时，﹣1＜x＜3；⑤a﹣b+c＞0，其中正确的说法有（　　）A．1个 B．2个 C．3个 D．4个19．如图，二次函数y＝ax2+bx+c（a≠0）的图象与x轴负半轴交于（﹣，0），对称轴为直线x＝1．有以下结论：①abc＞0；②3a+c＞0；③若点（﹣3，y1），（3，y2），（0，y3）均在函数图象上，则y1＞y3＞y2；④若方程a（2x+1）（2x﹣5）＝1的两根为x1，x2且x1＜x2，则x1＜﹣＜＜x2；⑤点M，N是抛物线与x轴的两个交点，若在x轴下方的抛物线上存在一点P，使得PM⊥PN，则a的范围为a≥﹣4．其中结论正确的有（　　）A．2个 B．3个 C．4个 D．5个20．二次函数y＝ax2+bx+c（a≠0）的大致图象如图所示，顶点坐标为（1，﹣4a），点A（4，y1）是该抛物线上一点，若点D（x2，y2）是抛物线上任意一点，有下列结论：①4a﹣2b+c＞0；②若y2＞y1，则x2＞4；③若0≤x2≤4，则0≤y2≤5a；④若方程a（x+1）（x﹣3）＝﹣1有两个实数根x1和x2，且x1＜x2，则﹣1＜x1＜x2＜3．其中正确结论的个数是（　　）A．1个 B．2个 C．3个 D．4个21．如图，二次函数y＝ax2+bx+c（a＞0）的图象与x轴交于A，B两点，与y轴的正半轴交于点C，它的对称轴为直线x＝﹣1，有下列结论：①abc＜0；②4ac﹣b2＜0；③c﹣a＞0；④当x＝﹣n2﹣2时，y≥c；⑤若x1，x2（x1＜x2）是方程ax2+bx+c＝0的两根，则方程a（x﹣x1）（x﹣x2）﹣1＝0的两根m，n（m＜n）满足m＜x1且n＞x2；其中，正确结论的个数是（　　）A．1 B．2 C．3 D．422．如图，二次函数y＝ax2+bx+c（a≠0）的图象过点（﹣2，0），对称轴为直线x＝1．有以下结论：①abc＞0；②8a+c＞0；③若A（x1，m），B（x2，m）是抛物线上的两点，当x＝x1+x2时，y＝c；④点M，N是抛物线与x轴的两个交点，若在x轴下方的抛物线上存在一点P，使得PM⊥PN，则a的取值范围为a≥；⑤若方程a（x+2）（4﹣x）＝﹣2的两根为x1，x2，且x1＜x2，则﹣2≤x1＜x2＜4．其中正确结论的序号是（　　）A．①②④ B．①③④ C．①③⑤ D．①②③⑤