2020-2021学年1 两数和乘以这两数的差示范课课件ppt

这是一份2020-2021学年1 两数和乘以这两数的差示范课课件ppt，共16页。

整式乘法中多项式与多项式相乘:1.多项式与多项式相乘，先用一个多项式的每一项乘另一个多项式的每一项，再把所得的积相加.符号表示：（m+b)(n+a)=mn+ma+bn+ba.2.两项式乘以两项式，结果可能是两项吗？
1.计算下列各式：(1)(x+2)(x-2) (2)(1+3a)(1-3a)(3)(x+5y)(x-5y) (4)(2y+z)(2y-z)（5）(a+b)(a-b)2.观察等号两边的代数式，它们在系数和字母方面各有什么特点？
【归纳结论】平方差公式：(a+b)(a-b)=a2-b2. 两数和与两数差的积，等于它们的平方差.
3.应用平方差公式的注意应注意些什么？（1）注意平方差公式的适用范围（2）字母a、b可以是数，也可以是整式（3）注意计算过程中的符号和括号
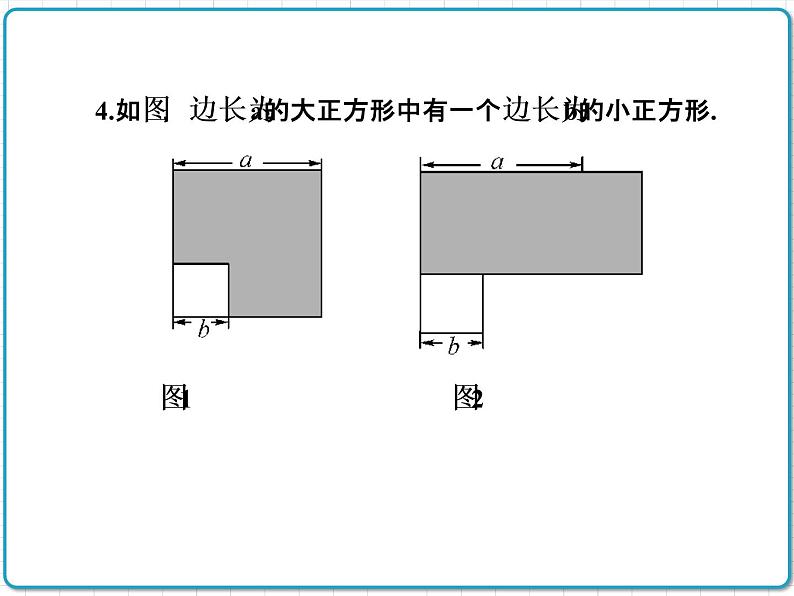
4.如图，边长为a的大正方形中有一个边长为b的小正方形.
图1 图2
表示图1中阴影部分的面积.②小颖将阴影部分拼成了一个长方形（如图2），这个长方形的长和宽分别是多少？你能表示出它的面积吗？③比较①，②的结果，你能验证平方差公式吗?④叙述平方差公式的数学表达式及文字表达式.⑤试比较公式的两种表达式在应用上的差异.
【归纳结论】(a+b)(a-b)=a2-b2
1.填空题(x+6)(6-x)= ，(-x+ )(-x- )= ，
(-2a2-5b)( )=4a2-25b2.
2.下列式中能用平方差公式计算的有( )
①(x- y)(x+ y)，
②(3a-bc)(-bc-3a)，③(3-x+y)(3+x+y)，④(100+1)(100-1).A.1个 B.2个 C.3个 D.4个
3.下列式中，运算正确的是( )①(22a)2=4a2；②(- x+1)(1+ x)=1- x2； ③(m-1)2(1-m)3=(m-1)5；④2a×4b×8=2a+2b+3.A.①② B.②③ C.②④ D.③④
4.乘法等式中的字母a、b表示( )A.只能是数B.只能是单项式C.只能是多项式D.数、单项式、多项式都可以
5.计算(a+1)(a-1)(a2+1)(a4+1)(a8+1).解：原式=(a2-1)(a2+1)(a4+1)(a8+1)=(a4-1)(a4+1)(a8+1)=(a8-1)(a8+1)=a16-1
6.计算：（1）（2a-b）（2a+b）（4a2+b2）；解：原式=（4a2-b2）（4a2+b2）=（4a2）2-（b2）2=16a4-b4.
（2）403×397解：原式=（400+3）（400-3）=4002-32=159991
通过这节课的学习活动，你有什么收获？