2020-2021学年5 边边边背景图课件ppt

这是一份2020-2021学年5 边边边背景图课件ppt，共17页。PPT课件主要包含了复习导入，推进新课，SSS，应用表达式如图，练习提升，随堂演练，证明连结AC，公共边，想一想，这节课你有什么收获等内容，欢迎下载使用。

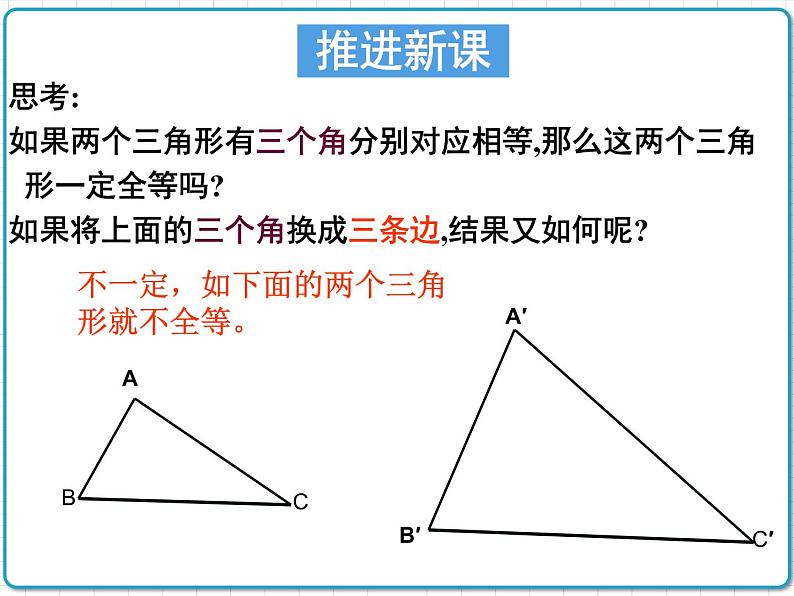
思考:如果两个三角形有三个角分别对应相等,那么这两个三角形一定全等吗?如果将上面的三个角换成三条边,结果又如何呢?
不一定，如下面的两个三角形就不全等。
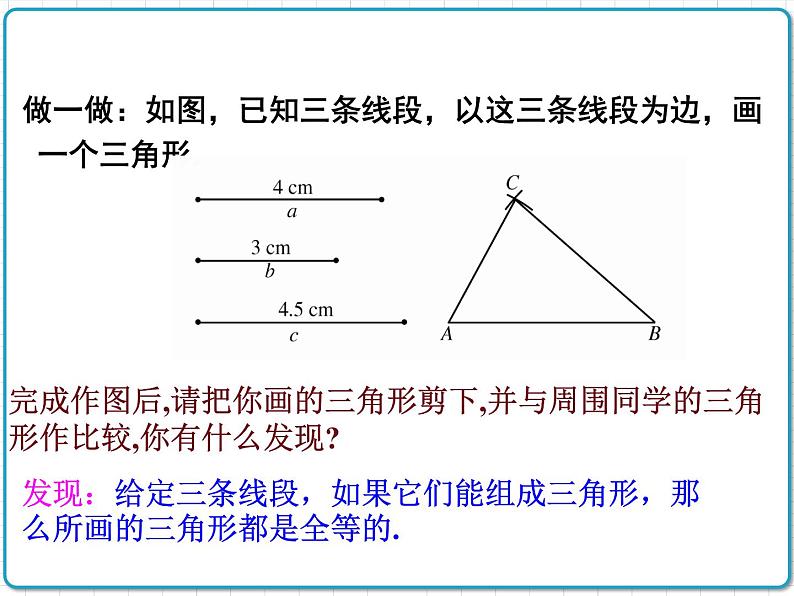
做一做：如图，已知三条线段，以这三条线段为边，画一个三角形．
完成作图后,请把你画的三角形剪下,并与周围同学的三角形作比较,你有什么发现?
发现：给定三条线段，如果它们能组成三角形，那么所画的三角形都是全等的.
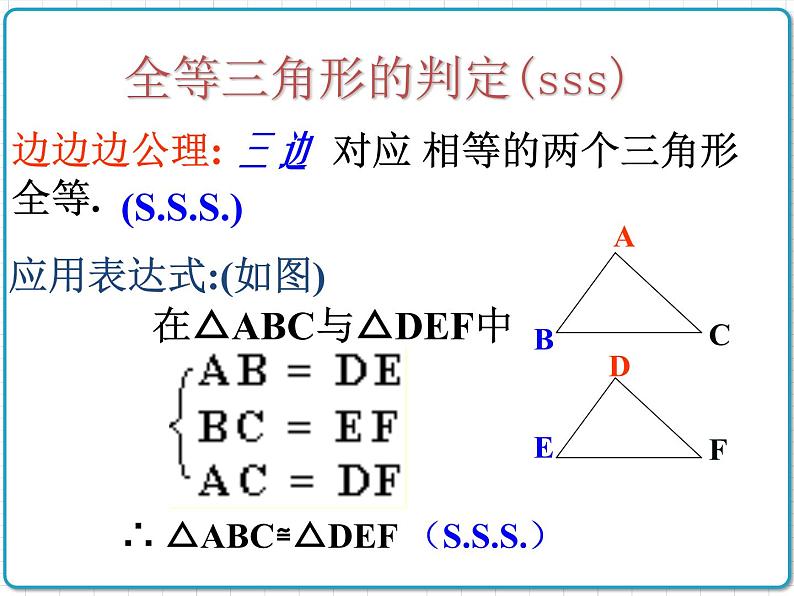
全等三角形的判定(sss)
边边边公理: 三边 对应 相等的两个三角形全等.
在△ABC与△DEF中
∴ △ABC≌△DEF （）
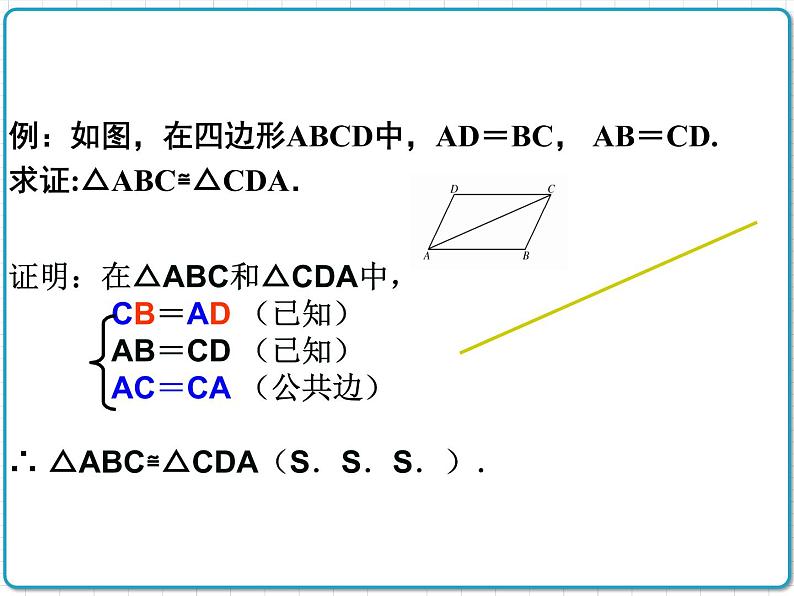
例：如图，在四边形ABCD中，AD＝BC， AB＝CD.求证:△ABC≌△CDA．
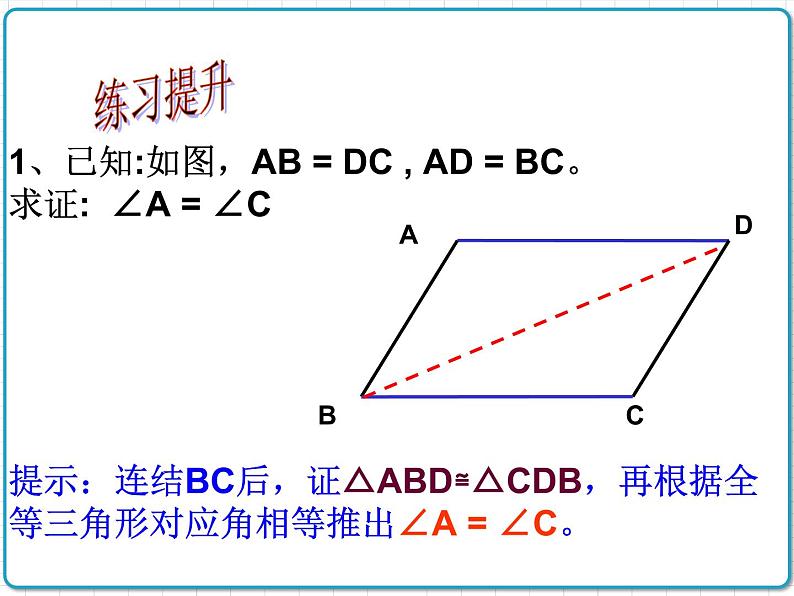
1、已知:如图，AB = DC , AD = BC。求证: ∠A = ∠C
提示：连结BC后，证△ABD≌△CDB，再根据全等三角形对应角相等推出∠A = ∠C。
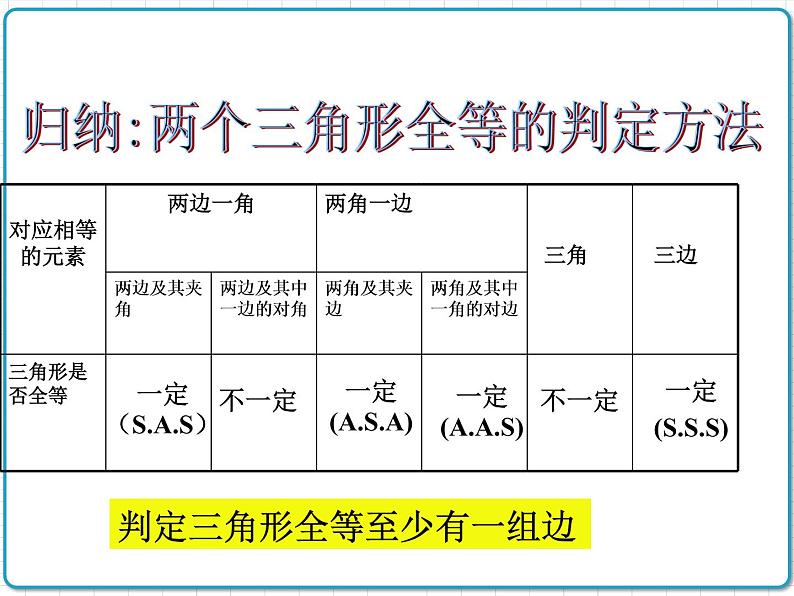
判定三角形全等至少有一组边
练习：1． 根据条件分别判定下面的三角形是否全等．（1） 线段AD与BC相交于点O，AO＝DO， BO＝CO. △ABO与△BCO；（2AC＝AD， BC＝BD. △ABC与△ABD；（3）∠A＝∠C， ∠B＝∠D. △ABO与△CDO（4） 线段AD与BC相交于点E，AE＝BE， CE＝DE， AC＝BD. △ABC与△BAD？
2． 如图，四边形ABCD是平行四边形，△ABC和△CDA是否全等？若四边形是菱形、矩形、梯形，是否还有相同的结论？
解：①全等（用或或或都能证得）
②因为菱形和矩形都是平行四边形，所以有相同的结论；而梯形不是平行四边形，所以没有相同的结论。
1、已知:如图.AB = DC , AC = DB求证: ∠A = ∠D
提示：BC为公共边，由可得两三角形全等，全等三角形对应角相等。
2、已知:如图.AB = AD ,BC = DC求证:∠B= ∠D
在△ABC与△ADC中
∴ △ABC≌△ADC （）
∴∠B=∠D（全等三角形对应角相等）
3、已知:如图.点B、 E、 C、 F在同一条直线上, AB = DE , AC = DF,BE = CF 求证: ∠A = ∠D
提示：因为BE+CE＝CF+CE，即BC＝EF，所以由得⊿ABC≌⊿DEF，所以∠A = ∠D（全等三角形对应角相等）
4、已知:如图.AB = DC , AC = DB，OA = OD求证:∠A = ∠D
证明：∵AC＝BD，OA＝OD，∴BD－OD＝AC－OA，即 OB＝OC.∵AB＝DC，OA＝OD，∴⊿OAB≌⊿ODC（）∴ ∠A = ∠D（全等三角形对应角相等）
5、已知：如图，△ABC是一个钢架，AB=AC， AD是连结A与BC中点D的支架. 求证：AD⊥BC
证明:在△ABD与△ACD中
∴ △ABD≌ △ACD ()
∴AD⊥BC (垂直定义)
∴∠1 = ∠2 (全等三角形的对应角相等)
请说出目前判定三角形全等的4种方法：