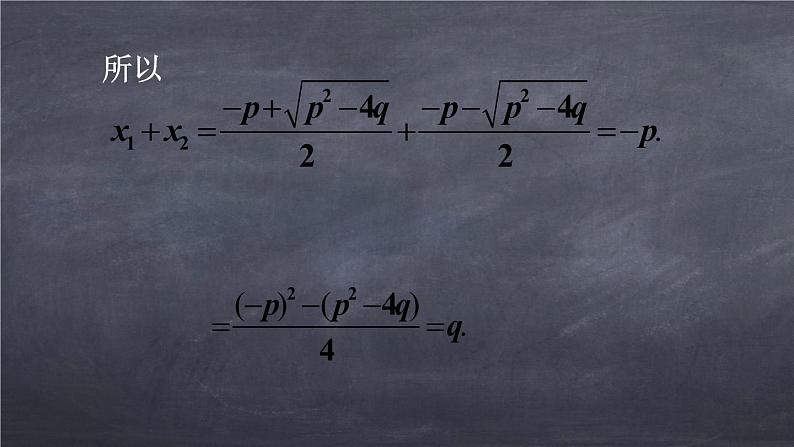
华师大版九年级上册5.一元二次方程的根与系数的关系评课课件ppt

这是一份华师大版九年级上册5.一元二次方程的根与系数的关系评课课件ppt，共17页。PPT课件主要包含了新课导入，二次项系数为1，一次项系数，常数项，相反数，推进新课，随堂演练，课堂小结，课后作业等内容，欢迎下载使用。
学习目标：1. 能运用根的判别式，判断方程根的情况和进行有关的推理论证；2. 会运用根的判别式求一元二次方程中字母系数的取值范围.
学习重点： 根的判别式的正确理解与运用.
学习难点： 含字母系数的一元二次方程根的判别式的应用.
求出一元二次方程 x2 + 3x – 4 = 0的两根 x1 和 x2，计算 x1 + x2 和 x1·x2 的值. 它们与方程的系数有什么关系？
x2 + 3x – 4 = 0 的两根为 x1 = 1 和 x2 = – 4，于是 x1 + x2 = – 3， x1·x2 = – 4.
x2 + 3x – 4 = 0
我们来考察方程 x2 + px + q = 0（p2 – 4q ≥ 0）.由一元二次方程的求根公式，得到方程的两根分别为
二次项系数为 1 的一元二次方程根与系数的关系：设一元二次方程 x2 + px + q = 0 的两根为x1、x2，那么x1 + x2 = – p ，x1·x2 = q.
不解方程，求出方程的两根之和和两根之积：（1）x2 + 3x – 5 = 0；（2）2x2 – 3x – 5 = 0；
（1）设两根为 x1、x2，由上述二次项系数为 1 的一元二次方程根与系数的关系，可得x1 + x2 = – 3 ，x1·x2 = – 5 .
（2）方程两边同除以 2 ，得
设两根为 x1、x2 ，可得
试探索一元二次方程 ax2 + bx + c = 0 (a ≠ 0，b2 – 4ac ≥ 0)的根与系数的关系.
方程两边同除以 a ，得
由二次项系数为 1 的一元二次方程根与系数的关系，可得
这就是一般情形下一元二次方程的根与系数的关系.
前面概括的结论是它的特例（二次项系数为1）.
1. 不解方程，求下列方程的两根之和与两根之积：（1）(x + 1)(x – 2) = 0；（2）3x2 + 7x = 6.
（1）x1 + x2 = 1，x1·x2 = – 2 .
x2 – x – 2 = 0
3x2 + 7x – 6 = 0
2. 两根均为负数的一元二次方程是（ ）A. 7x2 – 12x + 5 = 0B. 6x2 – 13x – 5 = 0C. 4x2 + 21x + 5 = 0D. x2 + 15x – 8 = 0
x1 + x2 < 0，x1·x2 > 0.
3.已知 α，β 是方程 x2 – 3x – 5 = 0的两根，不解方程，求下列代数式的值.
（2） α2 + β2 （3） α – β
（2）α2 + β2 = (α + β)2 – 2αβ = 32 – 2× (–5) = 19；（3）(α – β)2 = (α + β)2 – 4αβ = 29，
一元二次方程 ax2 + bx + c = 0 (a ≠ 0，b2 – 4ac ≥ 0)的根与系数的关系：
1.从教材习题中选取，2.完成练习册本课时的习题.