初中数学冀教版八年级上册17.2 直角三角形背景图ppt课件

这是一份初中数学冀教版八年级上册17.2 直角三角形背景图ppt课件，共20页。PPT课件主要包含了直角边，直角三角形的定义，∴∠A+∠B90°，几何语言，在△ABC中，°或135°，∵∠B300，等边三角形，４cm，２cm等内容，欢迎下载使用。

1.进一步认识直角三角形；会用符号和字母表示直角三角形.
2.掌握直角三角形两个锐角互余的性质；会用”两个锐角互余的三角形是直角三角形”这个判定方法判定直角三角形.
有一个角是直角的三角形叫做直角三角形.
直角三角形表示： Rt△
直角三角形ABC表示为Rt△ABC,∠ACB为Rt∠.
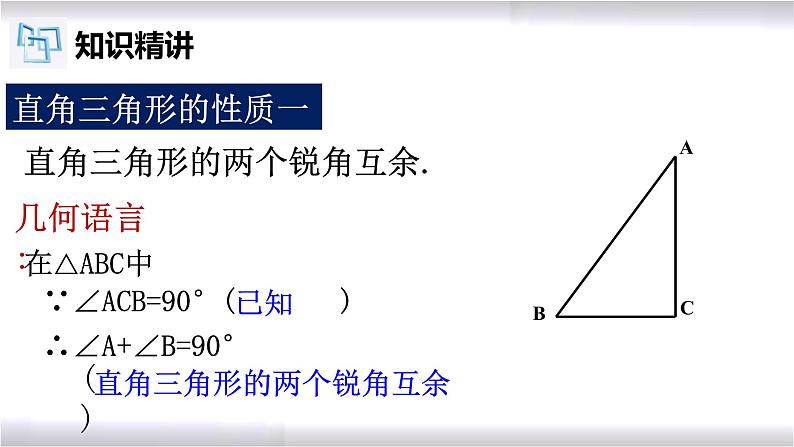
直角三角形的两个锐角互余.
∵∠ACB=90°( )
( )
直角三角形的两个锐角互余
1.△在ABC中,∠C=90°,∠A=30°,∠B= .
2.直角三角形两个锐角之差是10°，则较大的锐角是____度.
3.直角三角形的两个锐角的平分线所构成的角是 度.
4.一个三角形的三个内角之比是1：2：3 ,则这个三角形是 ______三角形.
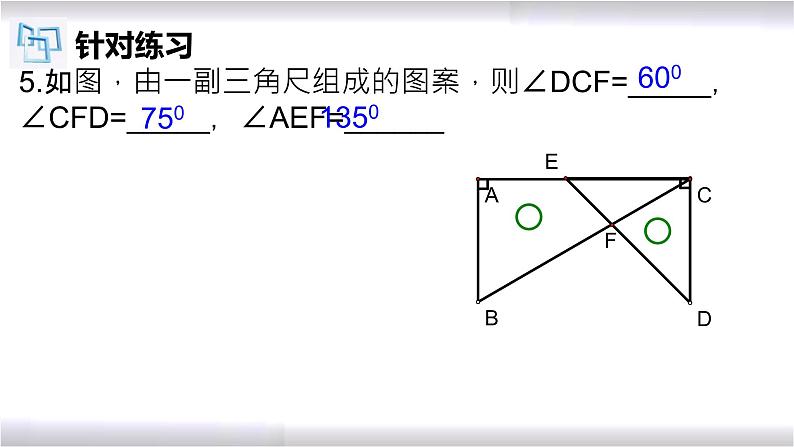
5.如图，由一副三角尺组成的图案，则∠DCF=_____，∠CFD=_____，∠AEF=______
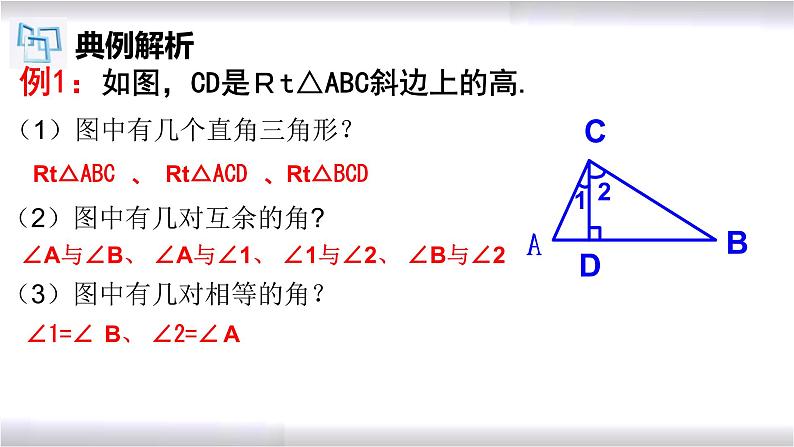
例1：如图，CD是Ｒt△ABC斜边上的高.
（1）图中有几个直角三角形？
Rt△ABC、 Rt△ACD、Rt△BCD
（2）图中有几对互余的角?
∠A与∠B、 ∠A与∠1、 ∠1与∠2、 ∠B与∠2
（3）图中有几对相等的角？
∠1=∠ B、 ∠2=∠A
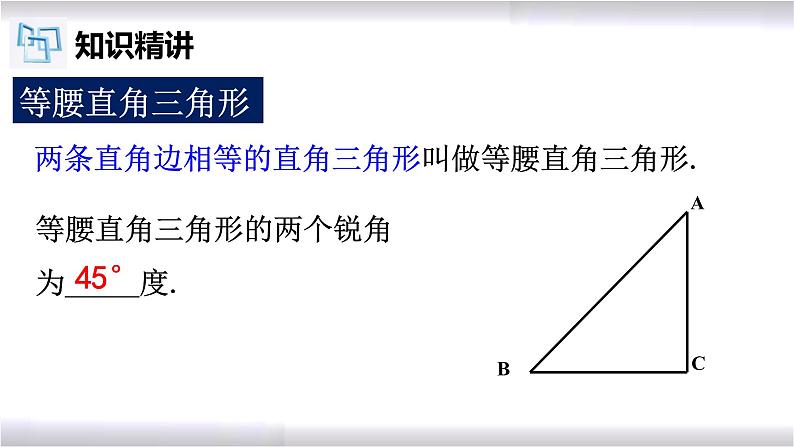
等腰直角三角形的两个锐角为_____度.
两条直角边相等的直角三角形叫做等腰直角三角形.
例2：如图，在等腰直角三角形ABC中，AD是斜边BC上的高，则AD=BD=CD.请说明理由.
证明：∵△ABC为等腰直角三角形∴∠B=∠C=45°，∠BAC=90°，AB=AC∵AD是斜边BC上的高∴∠ADB=∠ADC=90°，∠BAD=∠CAD=45°∴∠B=∠C=∠BAD=∠CAD∴AD=BD=CD.
证明:延长CD至E，使DE=CD，连结BE.∵CD是Rt △ ABC斜边AB上的中线∴AD=BD∵∠ADC=∠BDE∴△ADC≌△BDE(SAS)∴AC=BE,∠ACD=∠BED∴AC∥BE∴∠ACB+∠CBE=180°
直角三角形斜边上的中线等于斜边的一半.
∵ ∠ ACB=900 ，CD是AB边上的中线
∴CD= AB
例3 一名滑雪运动员沿着倾斜角为30°的斜坡，从A滑行至B.已知AB＝200m，问这名滑雪运动员的高度下降了多少m？
解：如图，作Rt△ABC的斜边上的中线CD，则
CD=AD=0.5AB=0.5×200=100m
（直角三角形斜边上的中线等于斜边的一半）
∴∠A=900－∠B=900－300=600
(直角三角形的两个锐角互余)
∴△ADC是等边三角形
(有一个角是600的等腰三角形是等边三角形)
∴AC=AD=100(m)
答:这名滑雪运动员的高度下降了100m.
1.已知Rt△ABC中，斜边AB=10cm，则斜边上的中线的长为______.
3.在Rt△ABC中,BD是斜边AC上的中线,∠A=30°.
(1)∠C=______∠ABD=_____ ∠BDC=______ ∠CBD=_____
(2) △BDC是什么三角形？
(3) 此时BC与AC有什么关系？
1.如图：在Rt△ABC中∠A=300,AB+BC=12cm，则AB=_____cm
2.如图:△ABC是等边三角形，AD⊥BC,DE⊥AB,若AB=8cm,BD=＿___，　BE=____.
3.如图，在△ABC,∠ACB=90°,CD⊥AB于D,∠A=30 °,则AD等于（ ）
A.4BD B.3BD C.2BD D.BD
4.如图，已知AD⊥BD，AC⊥BC，E为AB的中点，试判断DE与CE是否相等，并说明理由.
5.如图，已知AD、BE分别是△ABC的BC、AC边上的高，F是DE的中点，G是AB的中点，则FG⊥DE，请说明理由.