初中数学冀教版九年级上册25.5 相似三角形的性质课文配套课件ppt

这是一份初中数学冀教版九年级上册25.5 相似三角形的性质课文配套课件ppt，共22页。PPT课件主要包含了角平分线，以高为例，对应中线，对应角平分线，由前面的结论我们有，又∵∠D∠A，相似三角形的性质，相似三角形性质的运用等内容，欢迎下载使用。
1.理解并掌握相似三角形中对应线段的比和周长的比等于相似比，并运用其解决问题.
2.理解相似三角形面积的比等于相似比的平方，并运用其解决问题.
1. 相似三角形的判定方法有哪几种？
◑定义：对应边成比例，对应角相等的两个三角形相似.
◑平行于三角形一边，与另外两边相交所构成的三角形与原三角形相似.
◑三边成比例的两个三角形相似.
◑两边成比例且夹角相等的两个三角形相似.
◑两角分别相等的两个三角形相似.
◑一组直角边和斜边成比例的两个直角三角形相似.
2. 三角形除了三个角，三条边外，还有哪些要素?
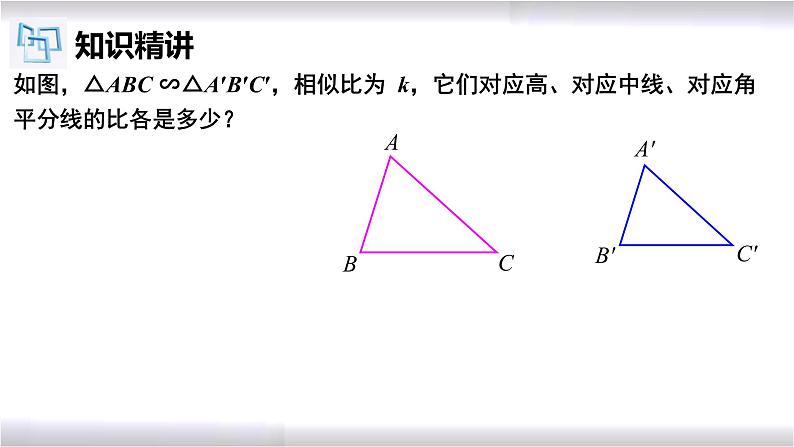
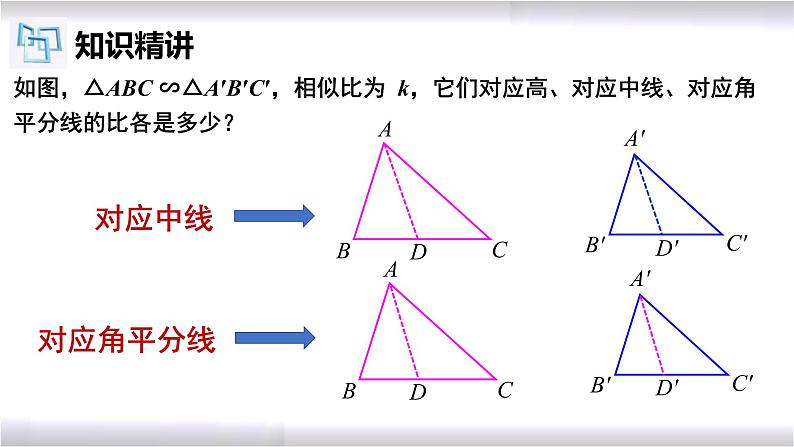
如图，△ABC ∽△A′B′C′，相似比为 k，它们对应高、对应中线、对应角平分线的比各是多少？
∵△ABC ∽△A′B′C′∴∠B＝∠B'
解：如图，分别作出 △ABC 和 △A' B' C' 的高 AD 和 A' D'
则∠ADB =∠A' D' B'=90°
∴△ABD ∽△A' B' D'
相似三角形对应线段的比
由此我们可以得到：
相似三角形对应高的比、对应中线与对应角平分线的比都等于相似比.
一般地，我们有：相似三角形对应线段的比等于相似比.
解：∵ △ABC ∽△DEF 　
例1 已知 △ABC∽△DEF，BG、EH 分别是 △ABC和 △DEF 的角平分线，BC = 6 cm，EF = 4cm，BG= 4.8 cm. 求 EH 的长.
∴ (相似三角形对应角平分线的比等于相似比)
∴ 故 EH 的长为 3.2 cm.
1. 如果两个相似三角形的对应高的比为 2 : 3，那么对应角平分线的比是 ，对应边上的中线的比是 ______.2. △ABC 与 △A’B’C’ 的相似比为3 : 4，若 BC 边上的高 AD＝12 cm，则 B’C’ 边上的高 A’D’ ＝_______ .
相似三角形的周长比也等于相似比吗？为什么？
解：如果 △ABC ∽△A'B'C'，相似比为 k，那么
如图，△ABC ∽△A′B′C′，相似比为 k，它们的面积比是多少？
相似三角形周长、面积的比
◑相似三角形面积的比等于相似比的平方.
◑相似三角形周长的比等于相似比.
解：在 △ABC 和 △DEF 中∵ AB=2DE，AC=2DF
∴ △DEF ∽ △ABC ，相似比为 1 : 2
△ABC 中，DE∥BC，EF∥AB，已知 △ADE 和△EFC 的面积分别为 4 和 9，求 △ABC 的面积.
解：∵ DE∥BC，EF∥AB∴ △ADE ∽△ABC,∠AED=∠C，∠A =∠CEF∴△ADE ∽△EFC又∵S△ADE : S△EFC = 4 : 9
∴ AE : EC=2:3则 AE : AC =2 : 5
∴ S△ADE : S△ABC = 4 : 25∴ S△ABC = 25
1. 判断： (1) 一个三角形的各边长扩大为原来的 5 倍，这个三角形的周长也扩大为原来的 5 倍 ( ) (2) 一个四边形的各边长扩大为原来的 9 倍，这个四边形的面积也扩大为原来的 9 倍 ( )
3. 连接三角形两边中点的线段把三角形截成的一个小三角形与原三角形的周长比等于______，面积比等于_____.
2. 在 △ABC 和 △DEF 中，AB＝2 DE，AC＝2 DF，∠A＝∠D，AP，DQ 是中线，若 AP＝2，则 DQ的值为( ) A．2 B．4 C．1 D.
4. 两个相似三角形对应的中线长分别是 6 cm 和 18 cm，若较大三角形的周长是 42 cm，面积是 12 cm2，则较小三角形的周长____cm，面积为____cm2.
5. 如图，这是圆桌正上方的灯泡 (点A) 发出的光线照 射桌面形成阴影的示意图，已知桌面的直径为 1.2 米，桌面距离地面为 1 米，若灯泡距离地面 3 米，则地面上阴影部分的面积约为多少 (结果保留两位小数)？
解：∵ FH = 1 米，AH = 3 米， 桌面的直径为 1.2 米， ∴ AF = AH－FH = 2 (米)， DF = 1.2÷2 = 0.6 (米). ∵DF∥CH， ∴△ADF ∽△ACH，
解得 CH = 0.9米.∴ 阴影部分的面积为：
答：地面上阴影部分的面积为 2.54 平方米.
相似三角形对应线段的比等于相似比
相似三角形面积的比等于相似比的平方