



初中数学冀教版九年级上册第26章 解直角三角形26.4 解直角三角形的应用教课内容课件ppt
展开1.能运用解直角三角形知识解决仰角和俯角、方向角、坡度有关的实际问题?
2.在解题过程中进一步体会数形结合、转化、方程的数学思想,并从这些问题中归纳出常见的基本模型及解题思路?
某探险者某天到达如图所示的点A 处时,他准备估算出离他的目的地,海拔为3 500 m的山峰顶点B处的水平距离。他能想出一个可行的办法吗?通过这节课的学习,相信你也行。
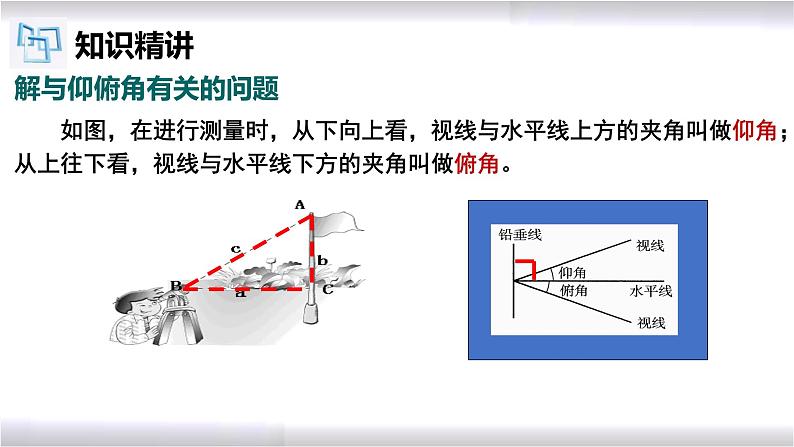
如图,在进行测量时,从下向上看,视线与水平线上方的夹角叫做仰角;从上往下看,视线与水平线下方的夹角叫做俯角。
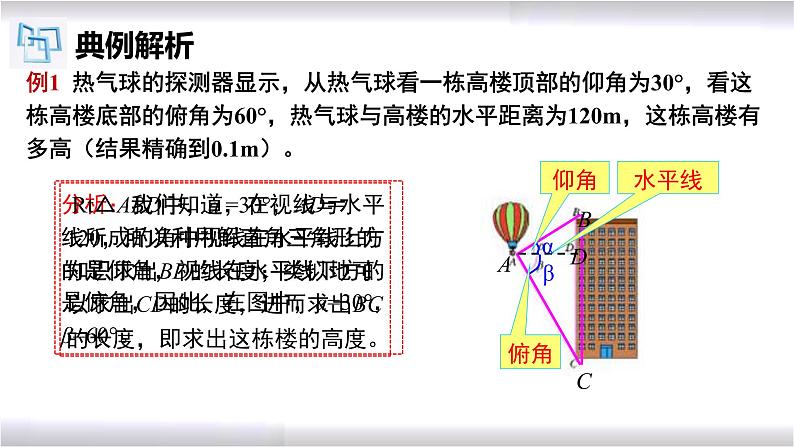
例1 热气球的探测器显示,从热气球看一栋高楼顶部的仰角为30°,看这栋高楼底部的俯角为60°,热气球与高楼的水平距离为120m,这栋高楼有多高(结果精确到0.1m)。
分析:我们知道,在视线与水平线所成的角中视线在水平线上方的是仰角,视线在水平线下方的是俯角,因此,在图中,a=30°,β=60°。
Rt△ABD中,a =30°,AD=120,所以利用解直角三角形的知识求出BD的长度;类似地可以求出CD的长度,进而求出BC的长度,即求出这栋楼的高度。
解:如图,a = 30°,β= 60°, AD=120。
答:这栋楼高约为277.1m。
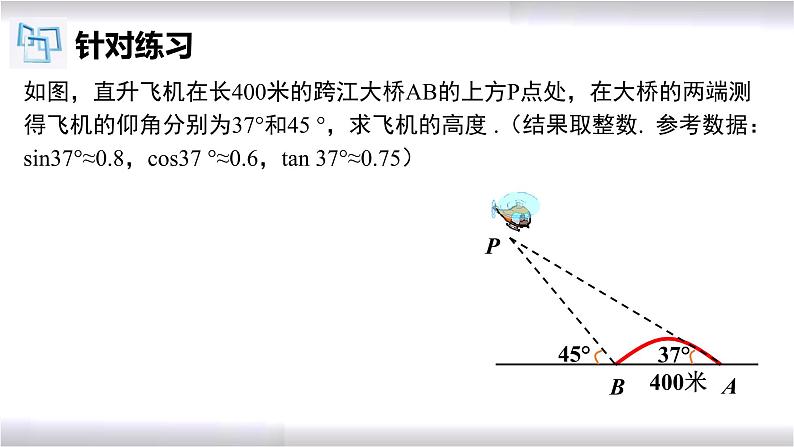
如图,直升飞机在长400米的跨江大桥AB的上方P点处,在大桥的两端测得飞机的仰角分别为37°和45 °,求飞机的高度 .(结果取整数. 参考数据:sin37°≈0.8,cs37 °≈0.6,tan 37°≈0.75)
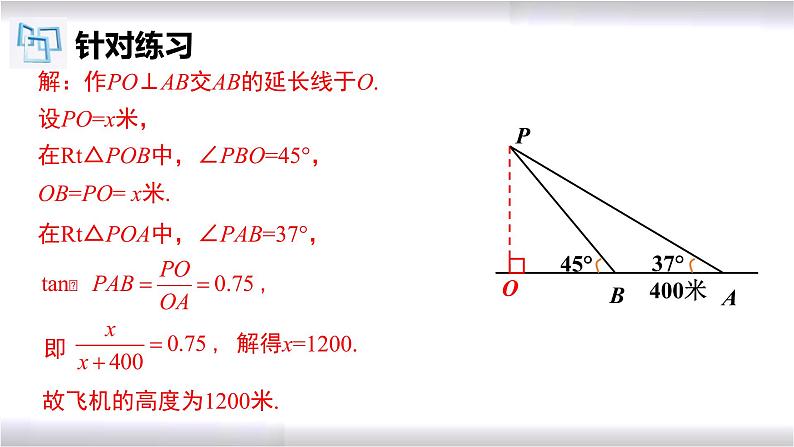
在Rt△POB中,∠PBO=45°,
在Rt△POA中,∠PAB=37°,
解:作PO⊥AB交AB的延长线于O.
故飞机的高度为1200米.
建筑物BC上有一旗杆AB,由距BC 40m的D处观察旗杆顶部A的仰角为54°,观察底部B的仰角为45°,求旗杆的高度(精确到0.1m)。
解:在等腰Rt△BCD中,∠ACD=90°,
∴AB=AC-BC=55.2-40=15.2 (m)
以正南或正北方向为准,正南或正北方向线与目标方向线构成的小于90°的角,叫做方位角。 如图所示:
例2 如图,一艘海轮位于灯塔P的北偏东65°方向,距离灯塔80 n mile的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东34°方向上的B处,这时,海轮所在的B处距离灯塔P有多远(精确到0.01 n mile)?
解:如图 ,在Rt△APC中,
PC=PA·cs(90°-65°)
在Rt△BPC中,∠B=34°,
因此,当海轮到达位于灯塔P的南偏东34°方向时,它距离灯塔P大约130n mile。
解:过A作AF⊥BC于点F, 则AF的长是A到BC的 最短距离. ∵BD∥CE∥AF, ∴∠DBA=∠BAF=60°, ∠ACE=∠CAF=30°, ∴∠BAC=∠BAF-∠CAF=60°-30°=30°.
例2 如图,海岛A的周围8海里内有暗礁,鱼船跟踪鱼群由西向东航行,在点B处测得海岛A位于北偏东60°,航行12海里到达点C处,又测得海岛A位于北偏东30°,如果鱼船不改变航向继续向东航行.有没有触礁的危险?
又∵∠ABC =∠DBF-∠DBA = 90°-60°=30°=∠BAC,∴BC=AC=12海里,∴AF=AC · cs30°=6 (海里),6 ≈10.392>8,故渔船继续向正东方向行驶,没有触礁的危险.
解:过点P作PC⊥AB,C是垂足. 则∠APC=30°,∠BPC=45°, AC=PC·tan30°,BC=PC·tan45°. ∵AC+BC=AB, ∴PC · tan30°+PC · tan45°=200, 即 PC+PC=200, 解得 PC≈126.8km>100km. 答:计划修筑的这条高速公 路不会穿越保护区.
如图,从山脚到山顶有两条路AB与BC,问哪条路比较陡?
如何用数量来刻画哪条路陡呢?
坡面与水平面的夹角叫做坡角,记作 α 。
2. 坡度 (或坡比)
坡度通常写成 1∶m的形式,如i=1∶6。
如图所示,坡面的铅垂高度 (h) 和水平长度 (l) 的比叫做坡面的坡度 (或坡比),记作i, 即 i = h : l 。
3. 坡度与坡角的关系
即坡度等于坡角的正切值。
1. 斜坡的坡度是 ,则坡角α =___度.2. 斜坡的坡角是45° ,则坡比是 _____.3. 斜坡长是12米,坡高6米,则坡比是_______.
解:作DE⊥AB,CF⊥AB,垂足分别为E、F。 由题意可知 DE=CF=4 (米),CD=EF=12 (米)。
一段路基的横断面是梯形,高为4米,上底的宽是12米,路基的坡面与地面的倾角分别是45°和30°,求路基下底的宽 (精确到0.1米, , )。
在Rt△ADE中,
在Rt△BCF中,同理可得因此 AB=AE+EF+BF≈4+12+6.93≈22.93 (米)。答: 路基下底的宽约为22.93米。
水库大坝的横断面是梯形,坝顶宽6m,坝高23m,斜坡AB的坡度i=1∶3,斜坡CD的坡度i=1∶2.5,求:(1) 斜坡CD的坡角α (精确到 1°);
解: 斜坡CD的坡度i = tanα = 1 : 2.5=0.4,由计算器可算得α≈22°.故斜坡CD的坡角α 为22°.
解:分别过点B、C作BE⊥AD,CF⊥AD,垂足分别为点E、 F,由题意可知BE=CF=23m, EF=BC=6m.
(2) 坝底AD与斜坡AB的长度 (精确到0.1m).
在Rt△ABE中,由勾股定理可得
故坝底AD的长度为132.5m,斜坡AB的长度为72.7m.
利用仰俯角解直角三角形
运用解直角三角形解决仰角、俯角问题
冀教版九年级上册26.4 解直角三角形的应用教学ppt课件: 这是一份冀教版九年级上册26.4 解直角三角形的应用教学ppt课件,文件包含教学课件九上·河北教育版·264解直角三角形的应用第2课时与坡度坡角有关的问题pptx、2642docx等2份课件配套教学资源,其中PPT共22页, 欢迎下载使用。
数学九年级上册第26章 解直角三角形26.4 解直角三角形的应用教学ppt课件: 这是一份数学九年级上册第26章 解直角三角形26.4 解直角三角形的应用教学ppt课件,文件包含教学课件九上·河北教育版·264解直角三角形的应用第1课时与仰角俯角及方向角有关的问题pptx、2641docx等2份课件配套教学资源,其中PPT共29页, 欢迎下载使用。
2021学年26.4 解直角三角形的应用教学演示ppt课件: 这是一份2021学年26.4 解直角三角形的应用教学演示ppt课件,共18页。PPT课件主要包含了解直角三角形,sinA=,cosA=,最远点等内容,欢迎下载使用。













