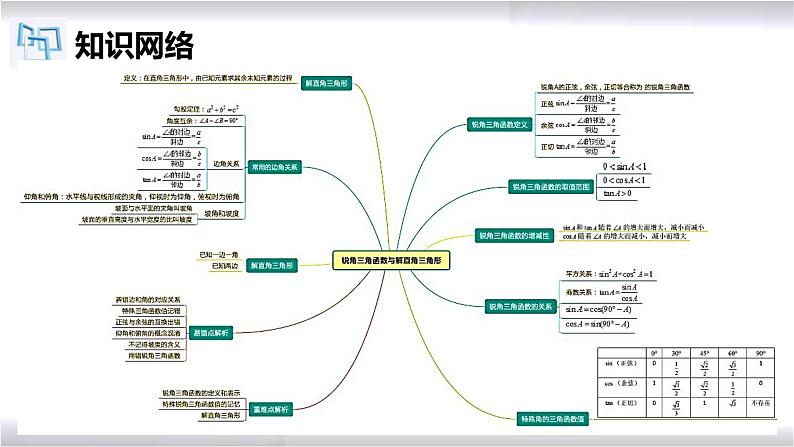
2021学年26.3 解直角三角形复习课件ppt

这是一份2021学年26.3 解直角三角形复习课件ppt，共34页。PPT课件主要包含了锐角三角函数，a2＋b2＝c2，∠A＝90°－∠B，解直角三角形，cos90°－α，sin90°－α，第二步输入角度值，屏幕显示结果，第二步输入函数值，方法①等内容，欢迎下载使用。

(2)∠A的余弦：csA＝　　　　　　＝　　　；(3)∠A的正切：tanA＝　　　　　　＝　　　.
如图所示，在Rt△ABC中，∠C＝90°，a，b，c分别是∠A，∠B，∠C的对边．
sin30°＝　　，sin45°＝　　，sin60°＝　　；cs30°＝　　，cs45°＝　　，cs60°＝　　；tan30°＝　　，tan45°＝　　，tan60°＝　　.
2. 特殊角的三角函数
(1) 在Rt△ABC中，∠C＝90°，a，b，c分别是∠A，∠B，∠C的对边．
三边关系：　 　；三角关系：　 ；边角关系：sinA＝csB＝　　　，csA＝sinB ＝ ，tanA＝　　　　　　，tanB＝　　　　　　.
(2) 直角三角形可解的条件和解法◑条件：解直角三角形时知道其中的2个元素(至少有一个是边)，就可以求出其余的3个未知元素．
◑解法：①一边一锐角，先由两锐角互余关系求出另一锐角；知斜边，再用正弦(或余弦)求另两边;知直角边用正切求另一直角边，再用正弦或勾股定理求斜边；②知两边：先用勾股定理求另一边，再用边角关系求锐角；③斜三角形问题可通过添加适当的辅助线转化为解直角三角形问题．
(3) 互余两角的三角函数间的关系
sinα = ，csα = ，sin2α + cs2α = .tanα · tan(90°－α) = .
对于sinα与tanα，角度越大，函数值越 ；对于csα，角度越大，函数值越 .
(4) 锐角三角函数的增减性
(1) 利用计算器求三角函数值
(也有的计算器是先输入角度再按函数名称键)
4. 借助计算器求锐角三角函数值及锐角
(2) 利用计算器求锐角的度数
还可以利用 键，进一步得到角的度数.
屏幕显示答案 (按实际需要进行精确)
第二步：输入锐角函数值
屏幕显示答案 (按实际需要选取精确值).
在进行测量时，从下向上看，视线与水平线的夹角叫做仰角；从上往下看，视线与水平线的夹角叫做俯角.
以正南或正北方向为准，正南或正北方向线与目标方向线构成的小于90°的角，叫做方位角. 如图所示：
坡面与水平面的夹角叫做坡角，记作α，有 i = tan α. 坡度通常写成1∶m的形式，如i=1∶6.显然，坡度越大，坡角α就越大，坡面就越陡.
如图：坡面的铅垂高度（h）和水平长度（l）的比叫做坡面坡度.记作i，即i = .
(4) 利用解直角三角形的知识解决实际问题的一般过程是： ① 将实际问题抽象为数学问题（画出平面图形，转化为解直角三角形的问题）； ② 根据条件的特点，适当选用锐角三角函数等去解直角三角形； ③ 得到数学问题的答案； ④ 得到实际问题的答案．
①在测点A安置测倾器，测得M的仰角∠MCE=α；
②量出测点A到物体底部N的水平距离AN=l；
③量出测倾器的高度AC=a，可求出 MN=ME+EN=l · tanα+a.
(1) 测量底部可以到达的物体的高度步骤：
6. 利用三角函数测高
考点一 求三角函数的值
【例1】在△ABC中，∠C＝90°，sinA＝ ，则tanB的值为 ( ) A.　　 B.　 　 C.　 　D.
【点睛】求三角函数值方法较多，解法灵活，在具体的解题中要根据已知条件采取灵活的计算方法，常用的方法主要有：(1)根据特殊角的三角函数值求值；(2)直接运用三角函数的定义求值；(3)借助边的数量关系求值；(4)借助等角求值；(5)根据三角函数关系求值；(6)构造直角三角形求值．
1. 在△ABC中， ∠A、 ∠B都是锐角，且sinA=csB，那么△ABC一定是______三角形．
2. 如图，在网格中，小正方形的边长均为1，点A，B，C都在格点上，则∠ABC的正切值是____.
【例2】矩形ABCD中AB=10，BC=8，E为AD边上一点，沿CE将△CDE对折，使点D正好落在AB边上，求tan∠AFE．
分析：根据题意，结合折叠的性质，易得∠AFE=∠BCF，进而在Rt△BFC中，有BC=8，CF=10，由勾股定理易得BF的长，根据三角函数的定义，易得 tan∠BCF的值，借助∠AFE=∠BCF，可得tan∠AFE的值．
解：由折叠的性质可得，CF=CD，∠EFC=∠EDC=90°.∵∠AFE+∠EFC+∠BFC=180°，∴∠AFE+∠BFC=90°.∵∠BCF+∠BFC=90°，∴∠AFE=∠BCF.在Rt△BFC中，BC=8，CF=CD=10，由勾股定理易得BF=6.
解：∵在直角△ABD中，tan∠BAD = ∴BD = AD·tan∠BAD=12× =9，∴CD=BC－BD=14－9=5，∴∴sinC =
考点二 特殊角的三角函数值
(1) tan30°＋cs45°＋tan60°；
(2) tan30°· tan60°＋ cs230°.
考点三 解直角三角形
【例4】 如图，在△ABC中，∠C＝90°，点D在BC上，BD＝4，AD＝BC，cs∠ADC = ，求：(1) DC的长；
分析：题中给出了两个直角三角形，DC和sinB可分别在Rt△ACD和Rt△ABC中求得，由AD＝BC，图中CD＝BC－BD，由此可列方程求出CD．
又 BC－CD＝BD，
解得x =6，∴CD=6.
(2) sinB的值．
解：BC=BD+CD=4+6=10=AD，
【点睛】本考点主要考查已知三角形中的边与角求其他的边与角.解决这类问题一般是结合方程思想与勾股定理，利用锐角三角函数进行求解.
如图所示，在Rt△ABC中，∠C＝90°，AC＝3. 点D为BC边上一点，且BD＝2AD，∠ADC＝60°.求△ABC的周长 (结果保留根号).
解：在Rt△ADC中，
∴BC＝BD＋DC＝5.
∴△ABC的周长为AB＋BC＋AC
【例5】已知：如图，Rt△AOB中，∠O＝90°，以OA为半径作⊙O，BC切⊙O于点C，连接AC交OB于点P.(1) 求证：BP＝BC；
解：连接OC.∵BC是⊙O的切线，∴∠OCB＝90°，∴∠OCA＋∠BCA＝90°.∵OA＝OC，∴∠OCA＝∠OAC，∴∠OAC＋∠BCA＝90°，∵∠BOA＝90°，∴∠OAC＋∠APO＝90°，∵∠APO＝∠BPC，∴∠BPC＝∠BCA，∴BC＝BP.
解：延长AO交⊙O于点E，连接CE，在Rt△AOP中，∵sin∠PAO＝ ，设OP＝x，AP＝3x，∴AO＝ x.∵AO＝OE，∴OE＝ x，∴AE＝ x.∵sin∠PAO＝ ，∴在Rt△ACE中 ，∴ ，解得x＝3，∴AO＝ x＝ ，即⊙O的半径为 .
如图，AB为⊙O的直径，且弦CD⊥AB于E，过点 B的切线与AD的延长线交于点F．若cs∠C = ，DF=3，求⊙O的半径．
在⊙O中，∠C=∠A，
∵BF是⊙O的切线，∴∠ABF=90°．
设AB=4x，则AF=5x，
由勾股定理得，BF=3x．
∵AB是⊙O的直径，∴BD⊥AD，
∴△ABF∽△BDF，
考点四 三角函数的应用
【例6】如图，防洪大堤的横截面是梯形 ABCD，其中AD∥BC，α=60°，汛期来临前对其进行了加固，改造后的背水面坡角β=45°．若原坡长AB=20m，求改造后的坡长AE．(结果保留根号)
解：过点A作AF⊥BC于点F，在Rt△ABF中，∠ABF =∠α=60°，则AF=AB·sin60°= (m)，在Rt△AEF中，∠E=∠β=45°，则 (m).
故改造后的坡长 AE 为 m.
如图，某防洪指挥部发现长江边一处防洪大堤 (横断面为梯形ABCD) 急需加固，背水坡的坡角为45°，高10米．经调查论证，防洪指挥部专家组制定的加固方案是：沿背水坡面用土石进行加固，并使上底加宽 2米，加固后背水坡EF的坡比i =1:　 ．求加固后坝底增加的宽度AF. (结果保留根号)
解：作DG⊥AB于G，EH⊥AB于G，则GH=DE=2米，EH=DG=10米.
又∵AG=DG=10米，
【例7】 如图所示，某数学活动小组选定测量小河对岸大树BC的高度，他们在斜坡上D处测得大树顶端B的仰角是30°，朝大树方向下坡走6米到达坡底A处，在A处测得大树顶端B的仰角是48°，若坡角∠FAE=30°，求大树的高度（结果保留整数，参考数据：sin48°≈0.74，cs48°≈0.67，tan48°≈1.11， ≈1.73）
解：如图，过点 D 作DG⊥BC于G，DH⊥CE于H，则四边形DHCG为矩形．故DG=CH，CG=DH，DG∥HC，∴∠DAH=∠FAE=30°，在直角三角形AHD中，∵∠DAH=30°，AD=6，∴DH=3，AH= ，∴CG=3，设BC为x，在直角三角形ABC中，
在Rt△BDG中，∵ BG=DG · tan30°，解得：x ≈13，∴大树的高度为：13米.
如图，为了测出某塔CD的高度，在塔前的平地上选择一点A，用测角仪测得塔顶D的仰角为30°，在A、C之间选择一点B（A、B、C三点在同一直线上）．用测角仪测得塔顶D的仰角为75°，且AB间的距离为40m． (1) 求点B到AD的距离；
答案：点B到AD的距离为20m.
(2) 求塔高CD（结果用根号表示）．
解：在Rt△ABE中，∵∠A=30°，∴∠ABE=60°，∵∠DBC=75°，∴∠EBD=180°－60°－75°=45°，∴DE=EB=20m，则AD=AE+EB= (m)，在Rt△ADC中，∠A=30°，答：塔高CD为 m.