数学八年级上册17.1 等腰三角形课文内容ppt课件

这是一份数学八年级上册17.1 等腰三角形课文内容ppt课件，共17页。PPT课件主要包含了三个角都相等，对称轴3条，等边三角形，对称轴1条，两个底角相等，且都是60º，两条边相等，三条边都相等，类比探究，不一定是等内容，欢迎下载使用。

1.探索等边三角形的判定.
2.能运用等边三角形的判定和性质进行计算和证明.
每一边上的中线、高和这一边所对的角的平分线互相重合
底边上的中线、高和顶角的平分线互相重合
三个角都相等的三角形是等边三角形
从角看：两个角相等的三角形是等腰三角形
从边看：两条边相等的三角形是等腰三角形
三条边都相等的三角形是等边三角形
小明认为还有第三种方法“两条边相等且有一个角是60°的三角形也是等边三角形”，你同意吗？
等边三角形的判定方法： 有一个角是60°的等腰三角形是等边三角形.
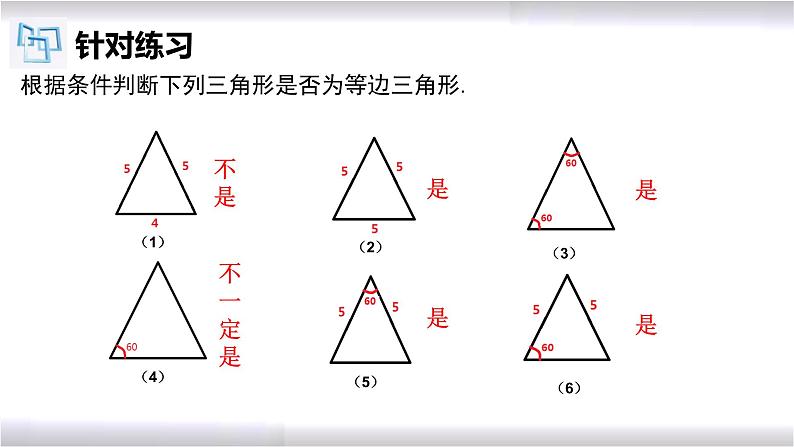
根据条件判断下列三角形是否为等边三角形.
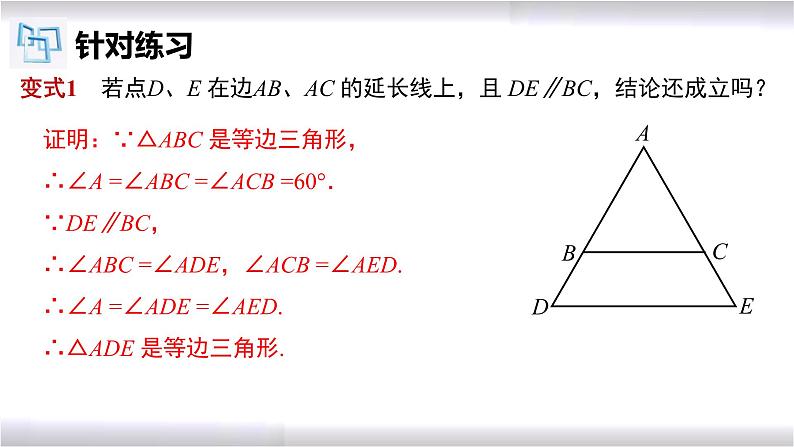
例1 如图,在等边三角形ABC中，DE∥BC, 求证：△ADE是等边三角形.
∵ △ABC是等边三角形，
∴ ∠A= ∠B= ∠C.
∴ ∠ADE= ∠B, ∠ AED= ∠C.
∴ ∠A= ∠ADE= ∠ AED.
∴ △ADE是等边三角形.
　证明：∵△ABC 是等边三角形， ∴∠A =∠ABC =∠ACB =60°． ∵DE∥BC， ∴∠ABC =∠ADE，∠ACB =∠AED. ∴∠A =∠ADE =∠AED. ∴△ADE 是等边三角形.
变式1　若点D、E 在边AB、AC 的延长线上，且 DE∥BC，结论还成立吗？
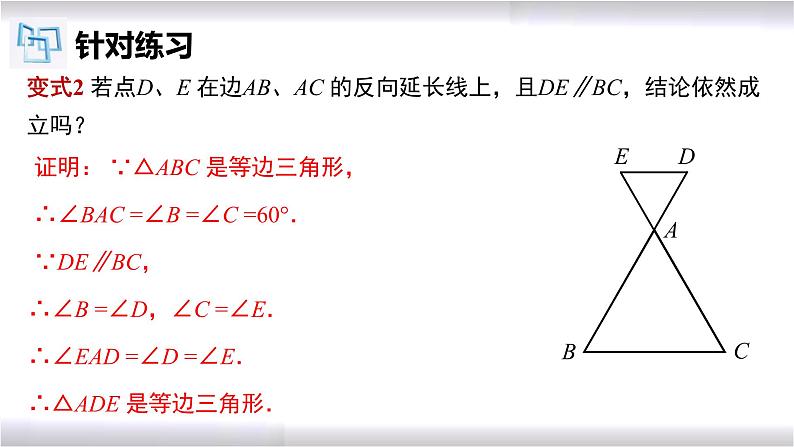
变式2 若点D、E 在边AB、AC 的反向延长线上，且DE∥BC，结论依然成立吗？
　　证明： ∵△ABC 是等边三角形， ∴∠BAC =∠B =∠C =60°． ∵DE∥BC， ∴∠B =∠D，∠C =∠E． ∴∠EAD =∠D =∠E． ∴△ADE 是等边三角形．
变式3 上题中,若将条件DE∥BC改为AD=AE, △ADE还是等边三角形吗?试说明理由.
例2 等边△ABC中，点P在△ABC内，点Q在△ABC外，且∠ABP＝∠ACQ，BP＝CQ，问△APQ是什么形状的三角形？试证明你的结论．
解：△APQ为等边三角形．证明如下：∵△ABC为等边三角形， ∴AB＝AC.∵BP＝CQ，∠ABP＝∠ACQ， ∴△ABP≌△ACQ(SAS)，∴AP＝AQ，∠BAP＝∠CAQ.∵∠BAC＝∠BAP＋∠PAC＝60°∴∠PAQ＝∠CAQ＋∠PAC＝60°∴△APQ是等边三角形．
【点睛】判定一个三角形是等边三角形有以下方法：一是证明三角形三条边相等；二是证明三角形三个内角相等；三是先证明三角形是等腰三角形，再证明有一个内角等于60°.
如图，等边△ABC中，D、E、F分别是各边上的一点，且AD=BE=CF．求证：△DEF是等边三角形．
证明：∵△ABC为等边三角形，且AD=BE=CF∴AF=BD=CE，∠A=∠B=∠C=60°，∴△ADF≌△BED≌△CFE（SAS），∴DF=ED=EF，∴△DEF是等边三角形．
如图，A、O、D三点共线，△OAB和△OCD是两个全等的等边三角形，求∠AEB的大小.
∵△OAB和△OCD是两个全等的等边三角形.
∴AO=BO,CO=DO, ∠AOB=∠COD=60°.
∵ A、O、D三点共线，
∴ ∠DOB=∠COA=120°，
∴ △COA≌△DOB(SAS).
∴ ∠DBO=∠CAO.
设OB与EA相交于点F,
∵ ∠EFB=∠AFO，
∴ ∠AEB=∠AOB=60°.
图①、图②中，点C为线段AB上一点，△ACM与△CBN都是等边三角形．(1)如图①，线段AN与线段BM是否相等？请说明理由；(2)如图②，AN与MC交于点E，BM与CN交于点F，探究△CEF的形状，并证明你的结论．
解：(1)AN＝BM.理由：∵△ACM与△CBN都是等边三角形，∴AC＝MC，CN＝CB，∠ACM＝∠BCN＝60°.∴∠ACN＝∠MCB.∴△ACN≌△MCB(SAS)．∴AN＝BM.
(1)如图①，线段AN与线段BM是否相等？请说明理由；
(2)△CEF是等边三角形．证明：∵∠ACE＝∠FCM=60°，∴∠ECF=60°.∵△ACN≌△MCB，∴∠CAE＝∠CMB.∵AC＝MC，∴△ACE≌△MCF(ASA)，∴CE＝CF. ∴△CEF是等边三角形．
(2)如图②，AN与MC交于点E，BM与CN交于点F，探究△CEF的形状，并证明你的结论．