






2021学年24.2 解一元二次方程授课ppt课件
展开1.了解配方的概念;掌握用配方法解一元二次方程及解决有关问题.
2.探索直接开平方法和配方法之间的区别和联系.
(1) 9x2=1 ;
(2) (x-2)2=2.
1.用直接开平方法解下列方程:
2.下列方程能用直接开平方法来解吗?
(1) x2+6x+9 =5;
(2)x2+4x+4=0.
把两题转化成(x+n)2=p(p≥0)的形式,再利用开平方
问题1:你还记得吗?填一填下列完全平方公式.
(1) a2+2ab+b2=( )2;
(2) a2-2ab+b2=( )2.
问题2:填上适当的数或式,使下列各等式成立.
(1)x2+4x+ = ( x + )2
(2)x2-6x+ = ( x- )2
(3)x2+8x+ = ( x+ )2
x2- x+ = ( x- )2
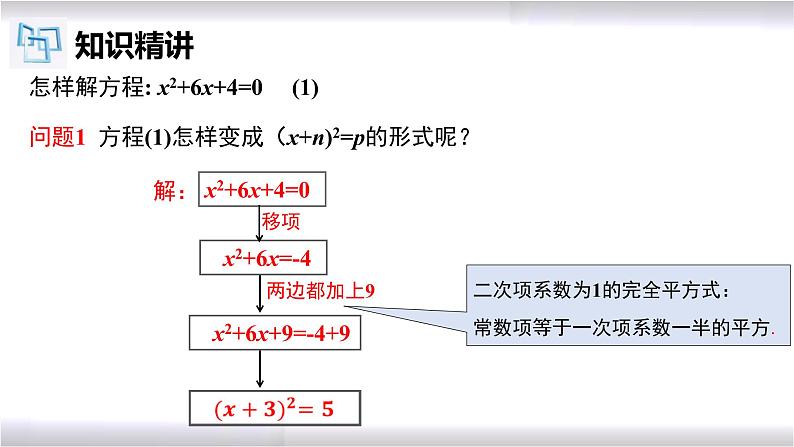
怎样解方程: x2+6x+4=0 (1)
问题1 方程(1)怎样变成(x+n)2=p的形式呢?
x2+6x=-4
x2+6x+9=-4+9
二次项系数为1的完全平方式: 常数项等于一次项系数一半的平方.
在方程两边都加上一次项系数一半的平方.注意是在二次项系数为1的前提下进行的.
问题2 为什么在方程x2+6x=-4的两边加上9?加其他数行吗?
不行,只有在方程两边加上一次项系数一半的平方,方程左边才能变成完成平方x2+2ax+a2的形式.
像上面这样通过配成完全平方式来解一元二次方程,叫做配方法.
※配方法解方程的基本思路
把方程化为(x+n)2=p的形式,将一元二次方程降次,转化为一元一次方程求解.
x2-8x+42=-1+42 ,
因为实数的平方不会是负数,所以x取任何实数时,上式都不成立,所以原方程无实数根.
思考1:用配方法解一元二次方程时,移项时要注意些什么?
思考2:用配方法解一元二次方程的一般步骤.
移项时需注意改变符号.
①移项,二次项系数化为1;②左边配成完全平方式;③左边写成完全平方形式;④降次;⑤解一次方程.
一般地,如果一个一元二次方程通过配方转化成 (x+n)2=p.
①当p>0时,则 ,方程的两个根为②当p=0时,则(x+n)2=0,x+n=0,开平方得方程的两个根为 x1=x2=-n.③当p<0时,则方程(x+n)2=p无实数根.
(1)x2+4x-9=2x-11; (2)x(x+4)=8x+12;(3)4x2-6x-3=0; (4) 3x2+6x-9=0.
解:x2+2x+2=0,
解:x2-4x-12=0,
x1=6,x2=-2;
解:x2+2x-3=0,
x1=-3,x2=1.
4.如图,在一块长35m、宽26m的矩形地面上,修建同样宽的两条互相垂直的道路,剩余部分栽种花草,要使剩余部分的面积为850m2,道路的宽应为多少?
解:设道路的宽为xm, 根据题意得
(35-x)(26-x)=850,
x2-61x+60=0.
x1=60(不合题意,舍去), x2=1.
把一元二次方程通过配成完全平方式来解一元二次方程,叫做配方法.
特别提醒:在使用配方法解方程之前先把方程化为x2+px+q=0的形式.
数学24.2 解一元二次方程多媒体教学课件ppt: 这是一份数学24.2 解一元二次方程多媒体教学课件ppt,共16页。PPT课件主要包含了解下列方程,解移项得,x2-8x-1,配方得,x-4215,由此可得,二次项系数化为1得,x2-3x-1,k-22+1,※配方法的应用等内容,欢迎下载使用。
初中数学冀教版九年级上册24.2 解一元二次方程图文课件ppt: 这是一份初中数学冀教版九年级上册24.2 解一元二次方程图文课件ppt,共20页。PPT课件主要包含了分解因式法,直接开平方法,配方法,公式法,mx2-nx0,xmx-n0,反过来,深入解析,b的和,b的积等内容,欢迎下载使用。
初中数学冀教版九年级上册24.2 解一元二次方程示范课ppt课件: 这是一份初中数学冀教版九年级上册24.2 解一元二次方程示范课ppt课件,共21页。PPT课件主要包含了因式分解,-49x0,因式分解法的概念,因式分解法的基本步骤,4x2x,例1解下列方程,于是得,解法选择基本思路,解化为一般式为,因式分解得等内容,欢迎下载使用。













