数学九年级上册28.3 圆心角和圆周角授课课件ppt

这是一份数学九年级上册28.3 圆心角和圆周角授课课件ppt，共20页。PPT课件主要包含了圆内接多边形，探究性质，延长BC到点E有，∴∠A＝∠DCE，∴x225°，∴∠ADB90°，∴AD⊥BC等内容，欢迎下载使用。

1.理解并掌握圆内接四边形的定义及性质.
2.能灵活运用圆内接四边形的性质解决相关问题.
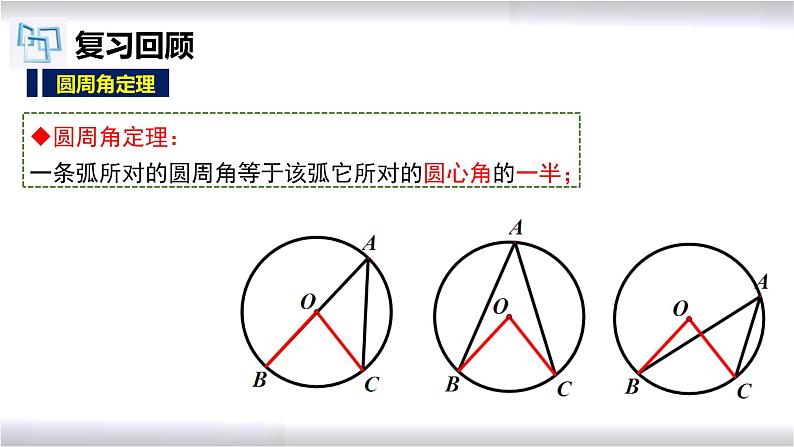
圆周角定理：一条弧所对的圆周角等于该弧它所对的圆心角的一半；
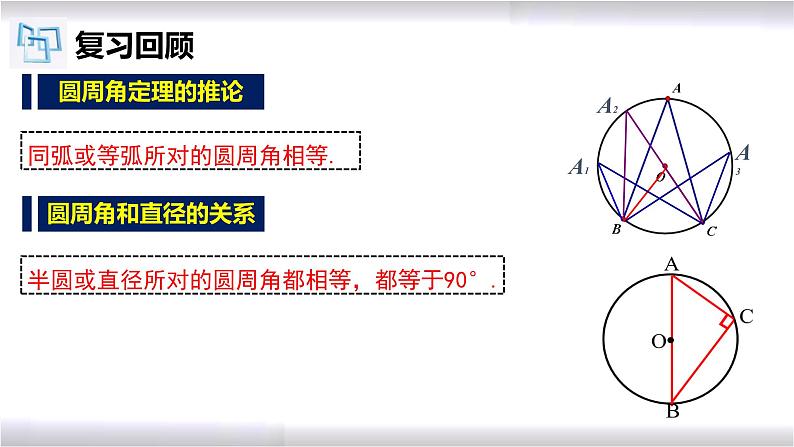
同弧或等弧所对的圆周角相等.
半圆或直径所对的圆周角都相等，都等于90°.
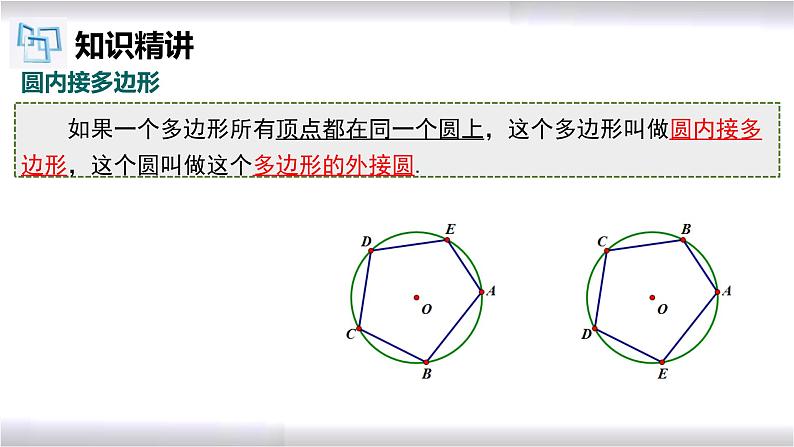
如果一个多边形所有顶点都在同一个圆上，这个多边形叫做圆内接多边形，这个圆叫做这个多边形的外接圆.
如图，四边形ABCD为⊙O的内接四边形，⊙O为四边形ABCD的外接圆.
猜想：∠A与∠C, ∠B与∠D之间的关系为：
∠A+ ∠C=180º，∠B+ ∠D=180º
思考：如何证明你的猜想呢？
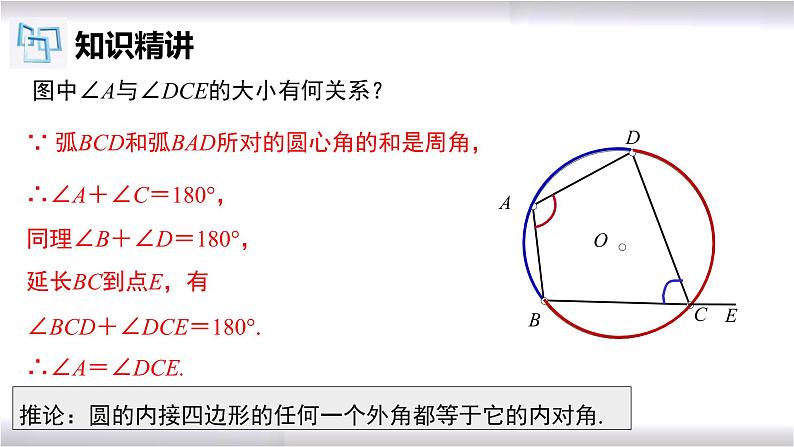
∵ 弧BCD和弧BAD所对的圆心角的和是周角，
∴∠A＋∠C＝180°，
同理∠B＋∠D＝180°.
推论：圆的内接四边形的对角互补.
同理∠B＋∠D＝180°，
∠BCD＋∠DCE＝180°.
图中∠A与∠DCE的大小有何关系？
推论：圆的内接四边形的任何一个外角都等于它的内对角.
1．四边形ABCD是⊙O的内接四边形，且∠A=110°，∠B=80°，则∠C= ，∠D= .2．⊙O的内接四边形ABCD中，∠A∶∠B∶∠C=1∶2∶3 ，则∠D= .
例1：如图，AB为⊙O的直径，CF⊥AB于E，交⊙O于D，AF交⊙O于G. 求证：∠FGD＝∠ADC.
证明：∵四边形ACDG内接于⊙O，∴∠FGD＝∠ACD.又∵AB为⊙O的直径，CF⊥AB于E，∴AB垂直平分CD，∴AC＝AD，∴∠ADC＝∠ACD，∴∠FGD＝∠ADC.
【点睛】圆内接四边形的性质是沟通角相等关系的重要依据．
如图，在⊙O的内接四边形ABCD中，∠BOD＝120°，那么∠BCD是(　　)A．120° B．100°C．80° D．60°
解析：∵∠BOD＝120°，∴∠A＝60°，∴∠C＝180°－60°＝120°，故选A.
解：设∠A，∠B，∠C的度数分别对于2x，3x，6x，
例2 在圆内接四边形ABCD中， ∠A，∠B，∠C的度数之比是2︰3︰6.求这个四边形各角的度数.
∵四边形ABCD内接于圆，
∴ ∠A+ ∠C=∠B+∠D=180°，
∵2x+6x=180°，
∴ ∠A=45°， ∠B=67.5°， ∠C =135°， ∠D=180°-67.5°=112.5°.
1.判断（1）同一个圆中等弧所对的圆周角相等 （ ）（2）相等的弦所对的圆周角也相等 （ ）（3）同弦所对的圆周角相等 （ ）
2.已知△ABC的三个顶点在⊙O上,∠BAC=50°,∠ABC=47°, 则∠AOB= ．
3.如图，已知BD是⊙O的直径，⊙O的弦AC⊥BD于点E，若∠AOD=60°，则∠DBC的度数为（ ） A.30° B.40° C.50° D.60°
4.如图，四边形ABCD内接于⊙O,如果∠BOD=130°,则∠BCD的度数是（ ） A 115° B 130° C 65° D 50°5.如图，等边三角形ABC内接于⊙O，P是AC上的一点，则∠APC= .
6.如图，已知圆心角∠AOB=100°,则圆周角∠ACB= ，∠ADB= .
7.如图，△ABC的顶点A、B、C都在⊙O上，∠C＝30 °，AB＝2，则⊙O的半径是 .
∵∠C=30 ° ，∴∠AOB=60 °
又∵OA=OB ，∴△AOB是等边三角形
∴OA=OB=AB=2，即半径为2.
∴∠ACB=2∠BAC
8. 如图，OA，OB，OC都是⊙O的半径，∠AOB=2∠BOC. 求证：∠ACB=2∠BAC.
∠AOB=2∠BOC，
∵AB是圆的直径，点D在圆上，
∵AB=AC， ∴BD=CD.
∵AD平分顶角∠BAC，即∠BAD=∠CAD，
（同圆或等圆中相等的圆周角所对弧相等）.
解:BD=CD.理由是:连接AD,
10.船在航行过程中，船长通过测定角数来确定是否遇到暗礁，如图，A、B表示灯塔，暗礁分布在经过A、B两点的一个圆形区域内，优弧AB上任一点C都是有触礁危险的临界点，∠ACB就是“危险角”，当船位于安全区域时，∠α与“危险角”有怎样的大小关系？
解：当船位于安全区域时，即船位于暗礁区域外（即⊙O外） ，与两个灯塔的夹角∠α小于“危险角”.
性质2：圆的内接四边形的任何一个外角都等于它的内对角.
性质1：圆的内接四边形的对角互补.