

华师大版八年级上册第14章 勾股定理综合与测试练习
展开2022-2023年华师大版数学八年级上册
第14章《勾股定理》单元检测卷
一 、选择题(本大题共12小题,每小题3分,共36分)
1.下列各组数为勾股数的是( )
A.6,12,13 B.3,4,7 C.4,7.5,8.5 D.8,15,16
2.已知一个直角三角形的两边长分别为3和4,则第三边长的平方是( )
A.25 B.14 C.7 D.7或25
3.已知Rt△ABC中,∠A,∠B,∠C的对边分别为a,b,c,若∠B=900,则( )
A.b2=a2+c2 ; B.c2=a2+b2; C.a2+b2=c2; D.a+b=c
4.如图,数轴上点A对应的数是0,点B对应的数是1,BC⊥AB,垂足为B,且BC=2,以A为圆心,AC为半径画弧,交数轴于点D,则点D表示的数为( )
A.2.2 B. C. D.
5.如图,点E在正方形ABCD内,满足∠AEB=90°,AE=6,BE=8,则阴影部分的面积是( )
A.48 B.60 C.74 D.80
6.如图,在边长为1个单位长度的小正方形组成的网格中,点A,B都是格点,则以AB为边的正方形的面积为( )
A.10 B.9 C.100 D.25
7.△ABC中,∠A,∠B,∠C的对边分别记为a,b,c,由下列条件不能判定△ABC为直角三角形的是( )
A.∠A:∠B:∠C=l:2:3
B.三边长为a,b,c的值为1,2,
C.三边长为a,b,c的值为,2,4
D.a2=(c+b)(c﹣b)
8.如图,在高为3米,斜坡长为5米的楼梯台阶上铺地毯,则地毯的长度至少要( )
A.4米 B.5米 C.6米 D.7米
9.如图,有两棵树,一棵高10米,另一棵高4米,两树相距8米,一只小鸟从一棵树的树梢飞到另一棵树的树梢,问小鸟至少飞行( )
A.8米 B.10米 C.12米 D.14米
10.如图一只蚂蚁从长宽都是3cm,高是8cm的长方体纸箱的A点沿纸箱爬到B点,那么它所行的最短路线的长是( )
A.13cm B.10cm C.14cm D.无法确定
11.在《算法统宗》中有一道“荡秋千”的问题:“平地秋千未起,踏板一尺离地.送行二步与人齐,五尺人高曾记.仕女佳人争蹴,终朝笑语欢嬉.良工高士素好奇,算出索长有几?”译文:“有一架秋千,当它静止时,踏板离地1尺,将它往前推送10尺(水平距离)时,秋千的踏板就和人一样高,这个人的身高为5尺,秋千的绳索始终拉得很直,试问绳索有多长?”.设这个人的身高是5尺,秋千的绳索始终拉的很直,则绳索长为( )
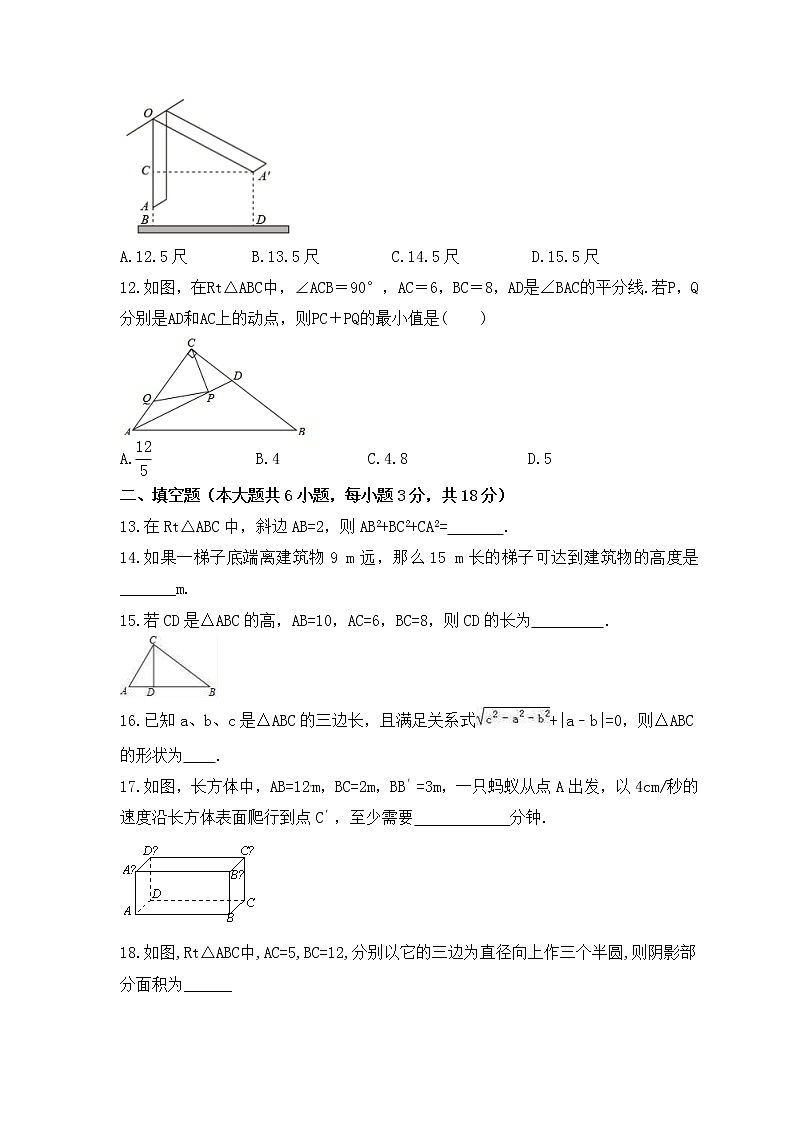
A.12.5尺 B.13.5尺 C.14.5尺 D.15.5尺
12.如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AD是∠BAC的平分线.若P,Q分别是AD和AC上的动点,则PC+PQ的最小值是( )
A. B.4 C.4.8 D.5
二 、填空题(本大题共6小题,每小题3分,共18分)
13.在Rt△ABC中,斜边AB=2,则AB2+BC2+CA2= .
14.如果一梯子底端离建筑物9 m远,那么15 m长的梯子可达到建筑物的高度是_______m.
15.若CD是△ABC的高,AB=10,AC=6,BC=8,则CD的长为 .
16.已知a、b、c是△ABC的三边长,且满足关系式+|a﹣b|=0,则△ABC的形状为 .
17.如图,长方体中,AB=12m,BC=2m,BB′=3m,一只蚂蚁从点A出发,以4cm/秒的速度沿长方体表面爬行到点C′,至少需要 分钟.
18.如图,Rt△ABC中,AC=5,BC=12,分别以它的三边为直径向上作三个半圆,则阴影部分面积为______
三 、作图题(本大题共1小题,共6分)
19.如图,正方形网格中的每个小正方形的边长都是1,每个小格的顶点叫作格点,以格点为顶点分别按下列要求画图形.
(1) 在图1中,画一个三角形,使它的三边长都是有理数;
(2) 在图2中,画一个直角三角形,使它们的三边长都是无理数;
(3) 在图3中,画一个正方形,使它的面积是10.
四 、解答题(本大题共6小题,共60分)
20.如图,已知△ABC中,∠C=90°,AB=10,BC=6,
(1)计算AC的长度;
(2)计算AB边上的中线CD的长度.
(3)计算AB边上的高CE的长度.
21.如图,方格纸中小正方形的边长为1,△ABC的三个顶点都在小正方形的格点上.
求:
(1)边AC,AB,BC的长;
(2)点C到AB边的距离;
(3)求△ABC的面积。
22.如图,在4×4的正方形网格中,每个小正方形的边长都是1.线段AB,AE分别是图中两个1×3的长方形的对角线,请你说明:AB⊥AE.
23.如图,已知∠ADC=90°,AD=8,CD=6,AB=26,BC=24.
(1)证明:△ABC是直角三角形.
(2)请求图中阴影部分的面积.
24.《中华人民共和国道路交通管理条例》规定:小汽车在城市道路上行驶速度不得超过70千米/时.如图,一辆小汽车在一条城市道路上直道行驶,某一时刻刚好行驶到车速检测仪正前方30米C处,过了2秒后,测得小汽车与车速检测仪间的距离为50米.
请问:这辆小汽车超速了吗?
25.如图,有5个边长为1的小正方形组成的纸片,可以把它剪拼成一个正方形.
(1) 拼成的正方形的面积是 ,边长是 ;
(2) 在数轴上作出表示、的点;
(3) 你能把这十个小正方形组成的图形纸,剪开并拼成一个大正方形吗?若能,在图中画出拼接后的正方形,并求边长,若不能,请说明理由.
参考答案
1.D
2.C
3.A
4.D.
5.C
6.A
7.C.
8.D
9.B
10.B.
11.C.
12.C
13.答案为:8 cm
14.答案为:12.
15.答案为:4.8.
16.答案为:等腰直角三角形.
17.答案为:3.25
18.答案为:30;
19.(1) 三边长分别为3,4,5 (如图1) (2) 三边长分别为,2, (如图2) (3) 画一个边长为的正方形(如图3)
20.解:
21.解:(1)AC=,AB=,BC=;
(2)点C到AB的距离是;
(3)3.5.
22.解:如图,连接BE.
因为AE2=12+32=10,AB2=12+32=10,
BE2=22+42=20,所以AE2+AB2=BE2.
所以△ABE是直角三角形,且∠BAE=90°,即AB⊥AE.
23.解:(1)证明:∵在Rt△ADC中,∠ADC=90°,AD=8,CD=6,
∴AC2=AD2+CD2=82+62=100,
∴AC=10(取正值).
在△ABC中,∵AC2+BC2=102+242=676,AB2=262=676,
∴AC2+BC2=AB2,
∴△ABC为直角三角形;
(2)解:S阴影=SRt△ABC﹣SRt△ACD
=×10×24﹣×8×6=96.
24.解:∵AC=30米,AB=50米,
在Rt△ABC中,由勾股定理得BC=40米,
∴小汽车速度为20米/秒=72千米/时>70千米/时,
∴小汽车超速了
25.解:(1)5 ,;(2)图略;(3)能.如图所示:变成为.
初中苏科版第三章 勾股定理综合与测试随堂练习题: 这是一份初中苏科版第三章 勾股定理综合与测试随堂练习题,共8页。试卷主要包含了选择题,填空题,作图题,解答题等内容,欢迎下载使用。
2021学年第12章 整式的乘除综合与测试课时训练: 这是一份2021学年第12章 整式的乘除综合与测试课时训练,共7页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
初中数学华师大版八年级上册第11章 数的开方综合与测试达标测试: 这是一份初中数学华师大版八年级上册第11章 数的开方综合与测试达标测试,共6页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。













