
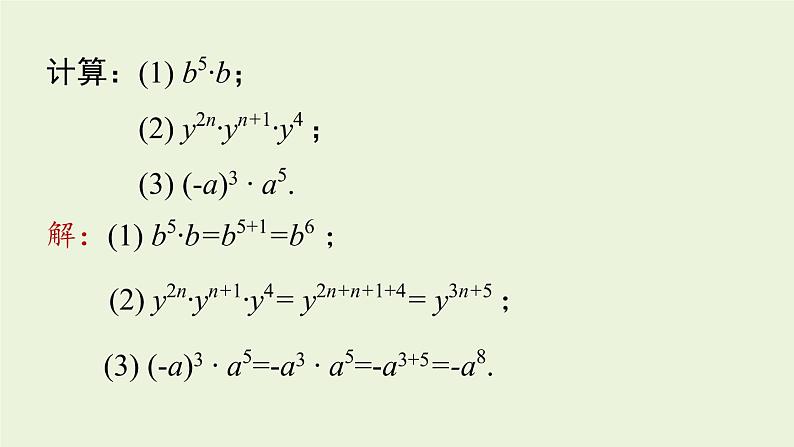



还剩14页未读,
继续阅读
14.1 整式的乘法课时2 初中数学人教版八年级上册实用课件
展开
这是一份14.1 整式的乘法课时2 初中数学人教版八年级上册实用课件,共22页。
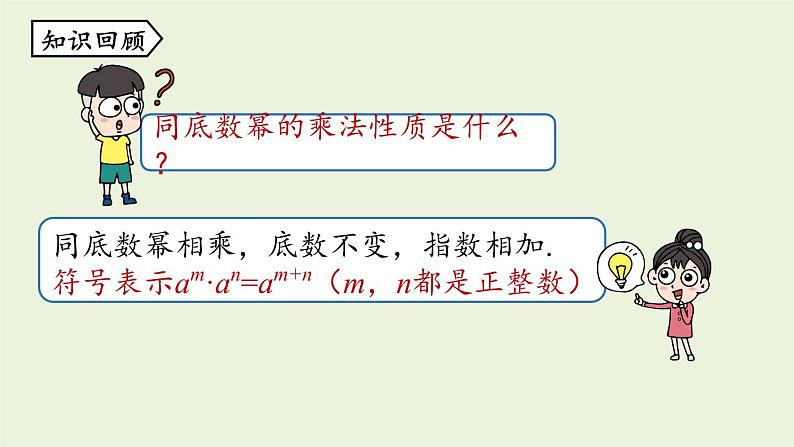
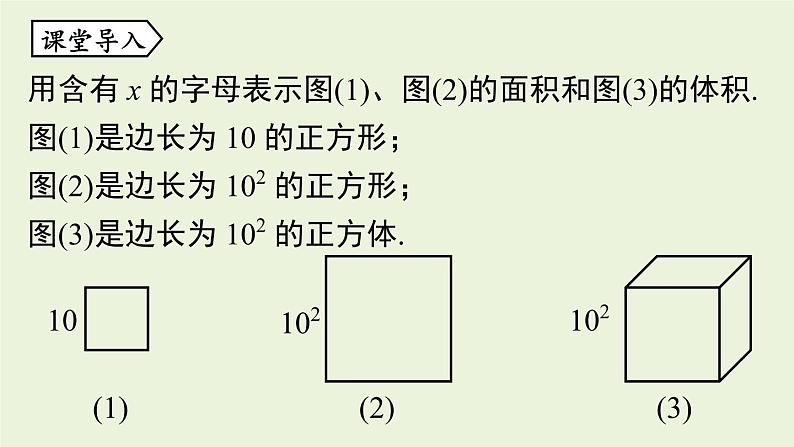
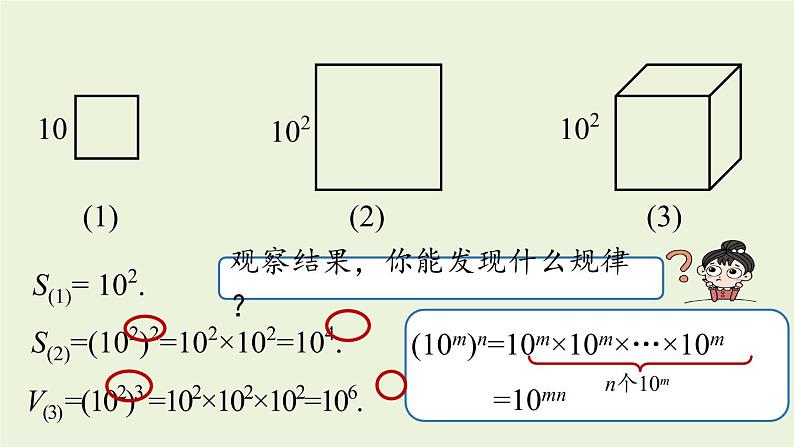
14.1.2 幂的乘方整式的乘法八年级上册 RJ初中数学知识回顾计算:(1) b5∙b; (2) y2n∙yn+1∙y4 ; (3) (-a)3 ∙ a5. 解:(1) b5∙b=b5+1=b6 ; (2) y2n∙yn+1∙y4= y2n+n+1+4= y3n+5 ; (3) (-a)3 ∙ a5=-a3 ∙ a5=-a3+5=-a8. 1.理解幂的乘方的性质,会利用这一性质进行幂的乘方运算.2.掌握幂的乘方的运算性质的推导.3.体会数式通性和从具体到抽象的思想方法在研究数学问题中的作用.学习目标用含有 x 的字母表示图(1)、图(2)的面积和图(3)的体积.图(1)是边长为 10 的正方形;图(2)是边长为 102 的正方形;图(3)是边长为 102 的正方体.课堂导入S(1)= 102.S(2)=(102)2=102×102=104.V(3) =(102)3 =102×102×102=106.根据乘方的意义及同底数幂的乘法填空(其中m,n为正整数):(1) (32)3=___________=3( );(2) (a2)3=________=a( );(3) (am)3=_________=a( );新知探究32×32×326 a2·a2·a26 am·am·am3m知识点 幂的乘方以上式子都是幂的乘方的形式,幂的乘方的结果中底数不变,指数相乘.一般地,对于任意底数a与任意正整数m,n,符号表示:(am)n=amn(m,n都是正整数).性质:幂的乘方,底数不变,指数相乘.幂的乘方=am·am·…·am=am+m+∙∙∙+m=amn. (am)n示例1: (a2)3=a2×3示例2: = (x+y) m×n[ (x+y) m]n 例 计算:(1) (103)5 ; (2) (a4)4 ; (3) (am)2 ; (4) -(x4)3 . 解:(1) (103)5=103×5=1015 ; (2) (a4)4 =a4×4=a16 ; (3) (am)2 = am×2= a2m ; (4) -(x4)3=-x4×3=-x12 . 跟踪训练新知探究底数不变底数不变指数相加指数相乘am·an=am+n(am)n=amn拓展: (1) 幂的乘方的性质也可以推广为三个及三个以上的幂的乘方,即 [(am)n]p=amnp(m,n,p都为正整数);(2) 幂的乘方的性质可以逆用,即 amn=(am)n (m,n为正整数). 随堂练习1.(2020·河北)若k为正整数,则(k+k+…+k)k=( )A. k2kB. k2k+1C. 2kkD. k2+kk个k(k·k)k(k2)kk2kA2.计算:(1) (103)3 ; (2) -(xm)5 ; (3) (a2)3·a5 ; (4) -[(a-b)7 ]2. 解:(1) (103)3=103×3=109 ; (2) -(xm)5=-xm×5=-x5m ; (3) (a2)3·a5=a2×3+5=a11 . (4) -[(a-b)7 ]2 = -(a-b)7×2= -(a-b)14 . 3.已知 a2n=3,求 a4n-a6n 的值.解:a4n-a6n = (a2n)2- (a2n)3= 32-33=-18 . 分析:把指数是积的形式的幂写成幂的乘方,如, amn=(am)n(m,n都是正整数),然后整体代入,求出式子的值.幂的乘方性质:幂的乘方,底数不变,指数相乘.(am)n=amn (m,n为正整数)课堂小结1.已知16m=4×22n-2,27n=9×3m+3 ,求 m,n 的值. 拓展提升1.已知16m=4×22n-2,27n=9×3m+3 ,求 m,n 的值. 拓展提升所以(24)m =22×22n-2 .所以4m=2n,即2m=n. ① 所以(33)n=32×3m+3 .所以3n=m+5. ② 2.比较 355,444 ,533 的大小.分析:观察可发现,这三个数的底数和指数均不相同,但指数都是11的整数倍,故可逆用幂的乘方的性质,将这三个数化成相同指数的幂,比较底数的大小,当指数、底数均大于0时,指数相同,底数越大则幂越大.2.比较 355 , 444 , 533 的大小.解: 355 = (35)11 = 24311 , 444 = (44)11 = 25611 , 533 = (53)11 = 12511 . 因为125<243<256, 所以12511<24311<25611 . 即 533<355< 444 .
14.1.2 幂的乘方整式的乘法八年级上册 RJ初中数学知识回顾计算:(1) b5∙b; (2) y2n∙yn+1∙y4 ; (3) (-a)3 ∙ a5. 解:(1) b5∙b=b5+1=b6 ; (2) y2n∙yn+1∙y4= y2n+n+1+4= y3n+5 ; (3) (-a)3 ∙ a5=-a3 ∙ a5=-a3+5=-a8. 1.理解幂的乘方的性质,会利用这一性质进行幂的乘方运算.2.掌握幂的乘方的运算性质的推导.3.体会数式通性和从具体到抽象的思想方法在研究数学问题中的作用.学习目标用含有 x 的字母表示图(1)、图(2)的面积和图(3)的体积.图(1)是边长为 10 的正方形;图(2)是边长为 102 的正方形;图(3)是边长为 102 的正方体.课堂导入S(1)= 102.S(2)=(102)2=102×102=104.V(3) =(102)3 =102×102×102=106.根据乘方的意义及同底数幂的乘法填空(其中m,n为正整数):(1) (32)3=___________=3( );(2) (a2)3=________=a( );(3) (am)3=_________=a( );新知探究32×32×326 a2·a2·a26 am·am·am3m知识点 幂的乘方以上式子都是幂的乘方的形式,幂的乘方的结果中底数不变,指数相乘.一般地,对于任意底数a与任意正整数m,n,符号表示:(am)n=amn(m,n都是正整数).性质:幂的乘方,底数不变,指数相乘.幂的乘方=am·am·…·am=am+m+∙∙∙+m=amn. (am)n示例1: (a2)3=a2×3示例2: = (x+y) m×n[ (x+y) m]n 例 计算:(1) (103)5 ; (2) (a4)4 ; (3) (am)2 ; (4) -(x4)3 . 解:(1) (103)5=103×5=1015 ; (2) (a4)4 =a4×4=a16 ; (3) (am)2 = am×2= a2m ; (4) -(x4)3=-x4×3=-x12 . 跟踪训练新知探究底数不变底数不变指数相加指数相乘am·an=am+n(am)n=amn拓展: (1) 幂的乘方的性质也可以推广为三个及三个以上的幂的乘方,即 [(am)n]p=amnp(m,n,p都为正整数);(2) 幂的乘方的性质可以逆用,即 amn=(am)n (m,n为正整数). 随堂练习1.(2020·河北)若k为正整数,则(k+k+…+k)k=( )A. k2kB. k2k+1C. 2kkD. k2+kk个k(k·k)k(k2)kk2kA2.计算:(1) (103)3 ; (2) -(xm)5 ; (3) (a2)3·a5 ; (4) -[(a-b)7 ]2. 解:(1) (103)3=103×3=109 ; (2) -(xm)5=-xm×5=-x5m ; (3) (a2)3·a5=a2×3+5=a11 . (4) -[(a-b)7 ]2 = -(a-b)7×2= -(a-b)14 . 3.已知 a2n=3,求 a4n-a6n 的值.解:a4n-a6n = (a2n)2- (a2n)3= 32-33=-18 . 分析:把指数是积的形式的幂写成幂的乘方,如, amn=(am)n(m,n都是正整数),然后整体代入,求出式子的值.幂的乘方性质:幂的乘方,底数不变,指数相乘.(am)n=amn (m,n为正整数)课堂小结1.已知16m=4×22n-2,27n=9×3m+3 ,求 m,n 的值. 拓展提升1.已知16m=4×22n-2,27n=9×3m+3 ,求 m,n 的值. 拓展提升所以(24)m =22×22n-2 .所以4m=2n,即2m=n. ① 所以(33)n=32×3m+3 .所以3n=m+5. ② 2.比较 355,444 ,533 的大小.分析:观察可发现,这三个数的底数和指数均不相同,但指数都是11的整数倍,故可逆用幂的乘方的性质,将这三个数化成相同指数的幂,比较底数的大小,当指数、底数均大于0时,指数相同,底数越大则幂越大.2.比较 355 , 444 , 533 的大小.解: 355 = (35)11 = 24311 , 444 = (44)11 = 25611 , 533 = (53)11 = 12511 . 因为125<243<256, 所以12511<24311<25611 . 即 533<355< 444 .
相关资料
更多









