14.2 乘法公式课时2 初中数学人教版八年级上册实用课件

这是一份14.2 乘法公式课时2 初中数学人教版八年级上册实用课件，共21页。

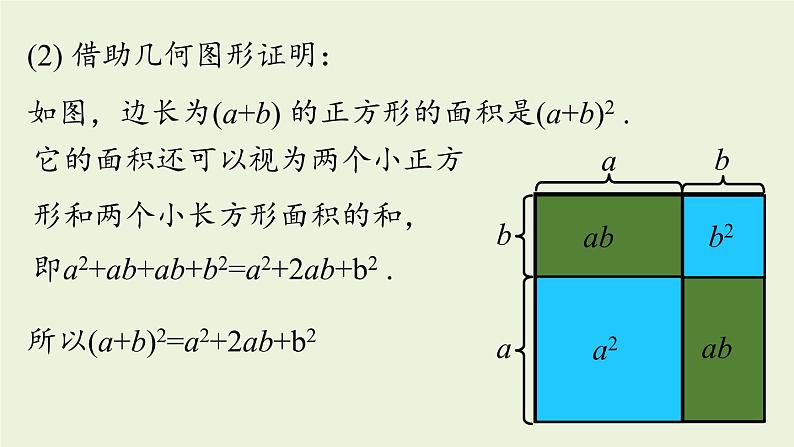
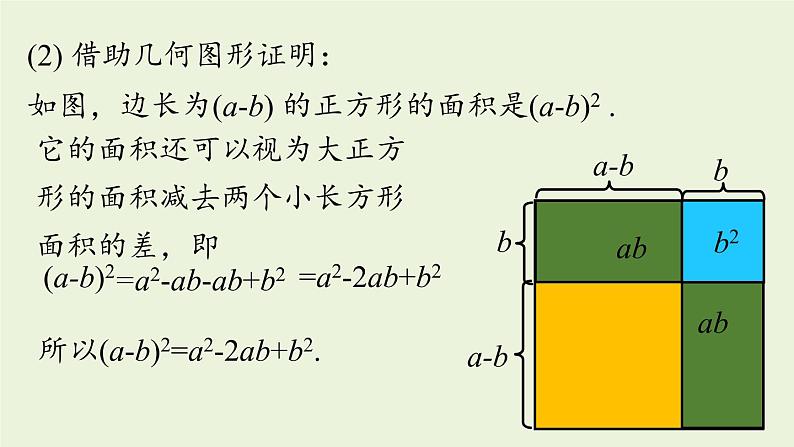
第1课时14.2.2　完全平方公式八年级上册 RJ初中数学平方差公式:(a+b)(a-b)=a2-b2.两个数的和两个数的差积平方差两个数的和与这两个数的差的积，等于这两个数的平方差.知识回顾1.了解并掌握完全平方公式.2.理解完全平方公式的推导过程，并会应用完全平方公式进行计算.学习目标课堂导入小明去市场买一种水果，价格为每公斤10.2元，现称出该水果为10.2斤，小明随即报出了要付现金104.04元.你知道小明为什么算得怎么快吗？计算下列多项式的积 (1) (p+1)2=__________=_________；p2+2p+1(2) (m+2)2=___________=_________；m2+4m+4(3) (p-1)2=__________=_________；p2-2p+1(4) (m-2)2=__________=_________；m2-4m+4知识点 完全平方公式新知探究(p+1)(p+1)(m+2)(m+2)(p-1)(p-1)(m-2)(m-2)猜想：(a+b)2=a2+2ab+b2；(a-b)2=a2-2ab+b2.m2+2×2m+22m2-2×2m+22p2+2p+12P2-2p+12(1)用多项式乘法证明：(a-b)2=(a-b)(a-b)(a+b)2=a2-ab-ab+b2=a2-2ab+b2=(a+b)(a+b)=a2+ab+ab+b2=a2+2ab+b2(2) 借助几何图形证明：如图，边长为(a+b) 的正方形的面积是(a+b)2 .它的面积还可以视为两个小正方形和两个小长方形面积的和，所以(a+b)2=a2+2ab+b2即a2+ab+ab+b2=a2+2ab+b2 . 它的面积还可以视为大正方形的面积减去两个小长方形面积的差，即如图，边长为(a-b) 的正方形的面积是(a-b)2 .所以(a-b)2=a2-2ab+b2.(2) 借助几何图形证明：(a-b)2a-b=a2-ab-ab+b2 =a2-2ab+b2 (a+b)2=a2+2ab+b2, (a-b)2=a2-2ab+b2. 两个数的和（或差）的平方，等于它们的平方和，加上（或减去）它们的积的2倍.完全平方公式特点：(1)两个公式的等号左边都是一个二项式的完全平方，两者仅有一个“符号”不同；(2)两个公式的等号右边都是二次三项式，其中首尾两项是等号左边二项式中每一项的平方，中间一项是左边二项式中两项乘积的2倍，两者也仅有一个“符号”不同. 解： (1) (4m+n)2 =(4m)2+2·4m·n+n2 =16m2+8mn+n2 ； 跟踪训练新知探究  (2) 992 =(100-1)2 =1002-2×100×1+12 =10 000-200+1 =9 801.完全平方公式的常见变形       (1)完全平方公式中的字母a，b可以是单项式，也可以是多项式，只要符合这个公式的结构特征就可以运用这个公式.(2)完全平方公式等号右边2ab的符号取决于等号左边二项式中两项的符号，若这两项同号，则2ab的符号为“+”；若这两项异号，则2ab的符号为“-”.(3)运用完全平方公式的时候要避免出现形如(a±b)2 = a2±b2 .随堂练习1.（2020·陕西）计算：(2x-y)2=（　　）A. 4x2-4xy+y2B. 4x2-2xy+y2C. 4x2-y2D. 4x2+y2(2x)2 -2·2x·y+y24x2 -4xy+y2A解：(1) (-2m-n)2 =(2m+n)2 =(2m)2+2·2m·n+n2 =4m2+4mn+n2 ；(2) (2x+3y)(-2x-3y) =-(2x+3y)2 =-[(2x)2+2·2x·3y+(3y)2] =-4x2-12xy-9y2 .2.计算下列式子：(1) (-2m-n)2 ； (2) (2x+3y)(-2x-3y) .解：(3) (-4a+5b)2 =(5b-4a)2 =(5b)2-2·5b·4a+(4a)2 =25b2-40ab+16a2 ；(4) (x+7y)2 =x2+2·x·7y+(7y)2 =x2+14xy+49y2 .2.计算下列式子：(3) (-4a+5b)2 ； (4) (x+7y)2 .3.（2020·枣庄）图1是一个长为2a，宽为2b(a＞b)的长方形，用剪刀沿图中虚线（对称轴）剪开，把它分成四块形状和大小都一样的小长方形，然后按图2那样拼成一个正方形，则中间空余的部分的面积是( )A. abB. (a+b)2C. (a-b)2D. a2-b2ab4ab(a+b)2C完全平方公式两个数的和（或差）的平方，等于它们的平方和，加上（或减去）它们的积的2倍(a+b)2=a2+2ab+b2,(a-b)2=a2-2ab+b2课堂小结1.将1052变形正确的是（ ）解： 1052=(100+5)2=1002+2×100×5+52.A. 1052=1002+52 B.1052=(100-5)(100+5)C. 1052=1002+2×100×5+52 D.1052=1002+100×5+52C拓展提升2.若(3x-a)2=9x2-bx+16，则a+b的值为（ ） A.28 B.-28 C.24或-24 D.28或-28D解：因为(3x-a)2=9x2-6ax+a2，所以9x2-6ax+a2=9x2-bx+16.则a2=16，6a=b,解得a=±4.当a=4时，b=24；当a=-4时，b=-24.所以a+b=28或-28. 3.已知m+n=8，mn=6，求m2+n2，(m-n)2 .分析：先将m2+n2，(m-n)2变形为用m+n, mn表示的式子，然后将已知整体代入求值.解：因为m+n=8，mn=6， 所以m2+n2=(m+n)2-2mn=82-2×6=52， m2-n2=(m+n)2-4mn=82-4×6=40.