(新高考)高考数学一轮复习学案8.3《直线、平面平行的判定与性质》(含详解)

这是一份(新高考)高考数学一轮复习学案8.3《直线、平面平行的判定与性质》(含详解)，共19页。学案主要包含了知识梳理，教材衍化等内容，欢迎下载使用。

第3讲　直线、平面平行的判定与性质


一、知识梳理
1．直线与平面平行的判定定理和性质定理

文字语言
图形语言
符号语言
判定
定理
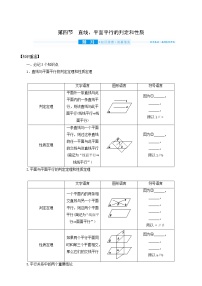
平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行(简记为“线线平行⇒线面平行”)

因为l∥a，
a⊂α，l⊄α，
所以l∥α
性质
定理
一条直线与一个平面平行，则过这条直线的任一平面与此平面的交线与该直线平行(简记为“线面平行⇒线线平行”)

因为l∥α，
l⊂β，
α∩β＝b，
所以l∥b
2.平面与平面平行的判定定理和性质定理

文字语言
图形语言
符号语言
判定
定理
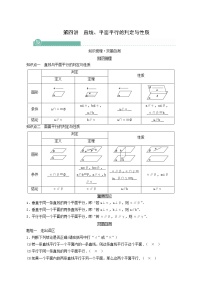
一个平面内的两条相交直线与另一个平面平行，则这两个平面平行(简记为“线面平行⇒面面平行”)

因为a∥β，
b∥β，a∩b＝P，
a⊂α，b⊂α，
所以α∥β
性质
定理
如果两个平行平面同时和第三个平面相交，那么它们的交线平行

因为α∥β，
α∩γ＝a，
β∩γ＝b，
所以a∥b
常用结论
1．三种平行关系的转化：
线线平行线面平行面面性质定理平行
线线平行、线面平行、面面平行的相互转化是解决与平行有关的证明题的指导思想．
2．平行关系中的三个重要结论
(1)垂直于同一条直线的两个平面平行，即若a⊥α，a⊥β，则α∥β.
(2)垂直于同一个平面的两条直线平行，即若a⊥α，b⊥α，则a∥b.
(3)平行于同一个平面的两个平面平行，即若α∥β，β∥γ，则α∥γ.
二、教材衍化
1．平面α∥平面β的一个充分条件是(　　)
A．存在一条直线a，a∥α，a∥β
B．存在一条直线a，a⊂α，a∥β
C．存在两条平行直线a，b，a⊂α，b⊂β，a∥β，b∥α
D．存在两条异面直线a，b，a⊂α，b⊂β，a∥β，b∥α
解析：选D．若α∩β＝l，a∥l，a⊄α，a⊄β，a∥α，a∥β，故排除A．若α∩β＝l，a⊂α，a∥l，则a∥β，故排除B．若α∩β＝l，a⊂α，a∥l，b⊂β，b∥l，则a∥β，b∥α，故排除C．
2．已知正方体ABCD­A1B1C1D1，下列结论中，正确的是________(只填序号)．
①AD1∥BC1；②平面AB1D1∥平面BDC1；③AD1∥DC1；④AD1∥平面BDC1.
解析：连接AD1，BC1，AB1，B1D1，C1D，BD，因为ABC1D1，所以四边形AD1C1B为平行四边形，

故AD1∥BC1，从而①正确；
易证BD∥B1D1，AB1∥DC1，
又AB1∩B1D1＝B1，BD∩DC1＝D，
故平面AB1D1∥平面BDC1，从而②正确；由图易知AD1与DC1异面．③错误；因为AD1∥BC1，AD1⊄平面BDC1，BC1⊂平面BDC1，故AD1∥平面BDC1，故④正确．
答案：①②④

一、思考辨析
判断正误(正确的打“√”，错误的打“×”)
(1)直线l平行于平面α内的无数条直线，则l∥α.(　　)
(2)若直线l在平面α外，则l∥α.(　　)
(3)若直线l∥b，直线b⊂α，则l∥α.(　　)
(4)若直线l∥b，直线b⊂α，那么直线l就平行于平面α内的无数条直线．(　　)
答案：(1)×　(2)×　(3)×　(4)√
二、易错纠偏
(1)对空间平行关系的相互转化条件理解不够；
(2)忽略线面平行、面面平行的条件．
1．如果直线a∥平面α，那么直线a与平面α内的(　　)
A．一条直线不相交　　　
B．两条直线不相交
C．无数条直线不相交
D．任意一条直线都不相交
解析：选D．因为a∥平面α，直线a与平面α无公共点，因此a和平面α内的任意一条直线都不相交，故选D．
2．如图是长方体被一平面所截得的几何体，四边形EFGH为截面，则四边形EFGH的形状为________．

解析：因为平面ABFE∥平面DCGH，又平面EFGH∩平面ABFE＝EF，平面EFGH∩平面DCGH＝HG，所以EF∥HG.同理EH∥FG，所以四边形EFGH是平行四边形．
答案：平行四边形

考点一　线面平行的判定与性质(基础型)
以立体几何的定义、公理和定理为出发点，认识和理解空间中直线与平面平行的有关性质与判定定理．
核心素养：直观想象、逻辑推理
角度一　线面平行的证明
在正方体ABCD­A1B1C1D1中，E，F，G，H分别是BC，CC1，C1D1，A1A的中点．求证：
(1)BF∥HD1；
(2)EG∥平面BB1D1D.
【证明】　(1)如图所示，取BB1的中点M，连接MH，MC1，易证四边形HMC1D1是平行四边形，

所以HD1∥MC1.
又因为在平面BCC1B1中，BMFC1，
所以四边形BMC1F为平行四边形，
所以MC1∥BF，
所以BF∥HD1.
(2)取BD的中点O，连接EO，D1O，
则OE∥DC且OE＝DC，
又D1G∥DC且D1G＝DC，
所以OED1G，
所以四边形OEGD1是平行四边形，
所以GE∥D1O.
又D1O⊂平面BB1D1D，GE⊄平面BB1D1D，
所以EG∥平面BB1D1D.

证明直线与平面平行的常用方法
(1)利用线面平行的定义．
(2)利用线面平行的判定定理：关键是找到平面内与已知直线平行的直线，可先直观判断题中是否存在这样的直线，若不存在，则需作出直线，常考虑利用三角形的中位线、平行四边形的对边平行或过已知直线作一平面，找其交线进行证明．　
角度二　线面平行性质的应用
如图，在五面体ABCDFE中，底面ABCD为矩形，EF∥AB，过BC的平面交棱FD于点P，交棱FA于点Q.
证明：PQ∥平面ABCD.

【证明】　因为底面ABCD为矩形，所以AD∥BC，
⇒BC∥平面ADF，
⇒BC∥PQ，
PQ∥平面ABCD.

应用线面平行的性质定理的关键是确定交线的位置，有时需要经过已知直线作辅助平面来确定交线．该定理的作用是由线面平行转化为线线平行．　

1．(2020·辽宁丹东质量测试(一))如图，直三棱柱ABC­A1B1C1中，∠BAC＝90°，AB＝AC＝2，D，E分别为AA1，B1C的中点．证明：DE∥平面ABC.

证明：取BC的中点F，
连接AF，EF，
则EF∥BB1，EF＝BB1，所以EF∥DA，EF＝DA，
则四边形ADEF为平行四边形，所以DE∥AF.
又因为DE⊄平面ABC，AF⊂平面ABC，所以DE∥平面ABC.
2．如图所示，已知四边形ABCD是正方形，四边形ACEF是矩形，AB＝2，AF＝1，M是线段EF的中点．

(1)求证：AM∥平面BDE；
(2)若平面ADM∩平面BDE＝l，平面ABM∩平面BDE＝m，试分析l与m的位置关系，并证明你的结论．
解：(1)证明：如图，记AC与BD的交点为O，连接OE.

因为O，M分别是AC，EF的中点，四边形ACEF是矩形，
所以四边形AOEM是平行四边形，所以AM∥OE.
又因为OE⊂平面BDE，AM⊄平面BDE，
所以AM∥平面BDE.
(2)l∥m，证明如下：由(1)知AM∥平面BDE，
又AM⊂平面ADM，平面ADM∩平面BDE＝l，
所以l∥AM，同理，AM∥平面BDE，
又AM⊂平面ABM，平面ABM∩平面BDE＝m，
所以m∥AM，所以l∥m.
考点二　面面平行的判定与性质
以立体几何的定义、公理和定理为出发点，认识和理解空间中平面与平面平行的有关性质与判定定理．
核心素养：逻辑推理、直观想象
如图所示，在三棱柱ABC­A1B1C1中，E，F，G，H分别是AB，AC，A1B1，A1C1的中点，求证：

(1)B，C，H，G四点共面；
(2)平面EFA1∥平面BCHG.
【证明】　(1)因为G，H分别是
A1B1，A1C1的中点，
所以GH∥B1C1，又B1C1∥BC，
所以GH∥BC，所以B，C，H，G四点共面．
(2)在△ABC中，E，F分别为AB，AC的中点，
所以EF∥BC，因为EF⊄平面BCHG，BC⊂平面BCHG，所以EF∥平面BCHG.
又因为G，E分别为A1B1，AB的中点，
所以A1GEB，所以四边形A1EBG是平行四边形，
所以A1E∥GB.
因为A1E⊄平面BCHG，GB⊂平面BCHG，
所以A1E∥平面BCHG.
又因为A1E∩EF＝E，所以平面EFA1∥平面BCHG.
【迁移探究1】　(变条件)在本例条件下，若D为BC1的中点，求证：HD∥平面A1B1BA.
证明：如图所示，连接HD，A1B，

因为D为BC1的中点，
H为A1C1的中点，所以HD∥A1B，
又HD⊄平面A1B1BA，
A1B⊂平面A1B1BA，
所以HD∥平面A1B1BA.
【迁移探究2】　(变条件)在本例条件下，若D1，D分别为B1C1，BC的中点，求证：平面A1BD1∥平面AC1D.
证明：如图所示，

连接A1C交AC1于点M，
因为四边形A1ACC1是平行四边形，
所以M是A1C的中点，连接MD，
因为D为BC的中点，
所以A1B∥DM.
因为A1B⊂平面A1BD1，DM⊄平面A1BD1，
所以DM∥平面A1BD1.
又由三棱柱的性质知，D1C1BD，
所以四边形BDC1D1为平行四边形，
所以DC1∥BD1.
又DC1⊄平面A1BD1，BD1⊂平面A1BD1，
所以DC1∥平面A1BD1，
又因为DC1∩DM＝D，DC1，DM⊂平面AC1D，
所以平面A1BD1∥平面AC1D.

　

1．如图，AB∥平面α∥平面β，过点A，B的直线m，n分别交α，β于点C，E和点D，F，若AC＝2，CE＝3，BF＝4，则BD的长为(　　)

A．　　　　　　　 B．
C． D．
解析：选C．由AB∥α∥β，易证 ＝.
即＝，所以BD＝＝＝.
2．(一题多解)如图，四边形ABCD是边长为3的正方形，ED⊥平面ABCD，AF⊥平面ABCD，DE＝3AF＝3.证明：平面ABF∥平面DCE.

证明：法一：因为DE⊥平面ABCD，AF⊥平面ABCD，
所以DE∥AF.
因为AF⊄平面DCE，DE⊂平面DCE，
所以AF∥平面DCE.
因为四边形ABCD是正方形，所以AB∥CD.
因为AB⊄平面DCE，
所以AB∥平面DCE.
因为AB∩AF＝A，AB⊂平面ABF，AF⊂平面ABF，
所以平面ABF∥平面DCE.
法二：因为DE⊥平面ABCD，AF⊥平面ABCD，
所以DE∥AF.
因为四边形ABCD为正方形，
所以AB∥CD.
又AF∩AB＝A，DE∩DC＝D，
所以平面ABF∥平面DCE.
法三：因为DE⊥平面ABCD，
所以DE⊥AD，在正方形ABCD中，AD⊥DC.
又DE∩DC＝D，
所以AD⊥平面DEC.
同理AD⊥平面ABF.
所以平面ABF∥平面DCE.
考点三　平行关系中的探索性问题
能运用公理、定理和已获得的结论证明一些有关空间图形的平行关系的简单命题．
核心素养：逻辑推理、直观想象
如图，已知斜三棱柱ABC­A1B1C1中，点D，D1分别为AC，A1C1上的点．

(1)当等于何值时，BC1∥平面AB1D1?
(2)若平面BC1D∥平面AB1D1，求的值．
【解】　(1)如图，取D1为线段A1C1的中点，此时＝1，

连接A1B交AB1于点O，连接OD1.
由棱柱的性质，知四边形A1ABB1为平行四边形，
所以点O为A1B的中点．
在△A1BC1中，点O，D1分别为A1B，A1C1的中点，
所以OD1∥BC1.
又因为OD1⊂平面AB1D1，BC1⊄平面AB1D1，
所以BC1∥平面AB1D1.
所以当＝1时，BC1∥平面AB1D1.
(2)由已知，平面BC1D∥平面AB1D1，
且平面A1BC1∩平面BDC1＝BC1，
平面A1BC1∩平面AB1D1＝D1O.
因此BC1∥D1O，同理AD1∥DC1.
因为＝，＝.
又因为＝1，所以＝1，即＝1.

解决探索性问题的方法
(1)根据探索性问题的设问，假设其存在并探索出结论，然后在这个假设下进行推理论证，若得到合乎情理的结论就肯定假设，若得到矛盾就否定假设．
(2)按类似于分析法的格式书写步骤：从结论出发“要使……成立”“只需使……成立”．　
　(一题多解)如图，四棱锥E­ABCD，平面ABCD⊥平面ABE，四边形ABCD为矩形，AD＝6，AB＝5，BE＝3，F为CE上的点，且BF⊥平面ACE.

(1)求证：AE⊥BE；
(2)设M在线段DE上，且满足EM＝2MD，试在线段AB上确定一点N，使得MN∥平面BCE，并求MN的长．
解：(1)证明：因为四边形ABCD为矩形，所以BC⊥AB.
因为平面ABCD⊥平面ABE，平面ABCD∩平面ABE＝AB，且BC⊂平面ABCD，
所以BC⊥平面ABE.
又AE⊂平面ABE，所以BC⊥AE.
因为BF⊥平面ACE，AE⊂平面ACE，
所以BF⊥AE.
又因为BC∩BF＝B，BC⊂平面BCE，BF⊂平面BCE，
所以AE⊥平面BCE，
因为BE⊂平面BCE，
所以AE⊥BE.
(2)法一：如图，在△ADE中过M点作MG∥AD交AE于G点，在△ABE中过G点作GN∥BE交AB于N点，连接MN，

因为NG∥BE，NG⊄平面BCE，BE⊂平面BCE，
所以NG∥平面BCE.
同理可证，GM∥平面BCE.
因为MG∩GN＝G，
所以平面MGN∥平面BCE，
又因为MN⊂平面MGN，
所以MN∥平面BCE，
因为N点为线段AB上靠近A点的一个三等分点，
AD＝6，AB＝5，BE＝3，
所以MG＝AD＝4，NG＝BE＝1，
所以MN＝＝＝.
法二：如图，过M点作MG∥CD交CE于G点，连接BG，在AB上取N点，使得BN＝MG，连接MN，
因为MG∥CD，EM＝2MD，
所以MG＝CD，
因为AB∥CD，BN＝MG，
所以四边形MGBN是平行四边形，
所以MN∥BG，
又因为MN⊄平面BCE，BG⊂平面BCE，

所以MN∥平面BCE，
又MG＝CD，MG＝BN，
所以BN＝AB，
所以N点为线段AB上靠近A点的一个三等分点．
在△CBG中，因为BC＝AD＝6，CG＝CE＝＝，cos∠BCG＝，
所以BG2＝36＋5－2×6××＝17，
所以MN＝BG＝.

[基础题组练]
1．若直线l不平行于平面α，且l⊄α，则(　　)
A．α内的所有直线与l异面
B．α内不存在与l平行的直线
C．α与直线l至少有两个公共点
D．α内的直线与l都相交
解析：选B．因为l⊄α，直线l不平行于平面α，所以直线l只能与平面α相交，于是直线l与平面α只有一个公共点，所以平面α内不存在与l平行的直线．
2．(2020·大连双基测试)已知直线l，m，平面α，β，γ，则下列条件能推出l∥m的是(　　)
A．l⊂α，m⊂β，α∥β B．α∥β，α∩γ＝l，β∩γ＝m
C．l∥α，m⊂α D．l⊂α，α∩β＝m
解析：选B．选项A中，直线l，m也可能异面；选项B中，根据面面平行的性质定理，可推出l∥m，B正确；选项C中，直线l，m也可能异面；选项D中，直线l，m也可能相交，故选B．
3．(2020·长沙市统一模拟考试)设a，b，c表示不同直线，α，β表示不同平面，下列命题：
①若a∥c，b∥c，则a∥b；②若a∥b，b∥α，则a∥α；③若a∥α，b∥α，则a∥b；④若a⊂α，b⊂β，α∥β，则a∥b.
真命题的个数是(　　)
A．1 B．2
C．3 D．4
解析：选A．由题意，对于①，根据线线平行的传递性可知①是真命题；对于②，根据a∥b，b∥α，可以推出a∥α或a⊂α，故②是假命题；对于③，根据a∥α，b∥α，可以推出a与b平行、相交或异面，故③是假命题；对于④，根据a⊂α，b⊂β.α∥β，可以推出a∥b或a与b异面，故④是假命题，所以真命题的个数是1，故选A．
4.如图所示，在空间四边形ABCD中，E，F分别为边AB，AD上的点，且AE∶EB＝AF∶FD＝1∶4，又H，G分别为BC，CD的中点，则(　　)

A．BD∥平面EFGH，且四边形EFGH 是矩形
B．EF∥平面BCD，且四边形EFGH是梯形
C．HG∥平面ABD，且四边形EFGH是菱形
D．EH∥平面ADC，且四边形EFGH是平行四边形
解析：选B．由AE∶EB＝AF∶FD＝1∶4知EFBD，又EF⊄平面BCD，所以EF∥平面BCD.又H，G分别为BC，CD的中点，所以HGBD，所以EF∥HG且EF≠HG.所以四边形EFGH是梯形．
5.在正方体ABCD­A1B1C1D1中，E，F，G分别是A1B1，B1C1，BB1的中点，给出下列四个推断：

①FG∥平面AA1D1D；②EF∥平面BC1D1；③FG∥平面BC1D1；④平面EFG∥平面BC1D1.
其中推断正确的序号是(　　)
A．①③ B．①④
C．②③ D．②④
解析：选A．因为在正方体ABCD­A1B1C1D1中，E，F，G分别是A1B1，B1C1，BB1的中点，所以FG∥BC1，因为BC1∥AD1，所以FG∥AD1，
因为FG⊄平面AA1D1D，AD1⊂平面AA1D1D，所以FG∥平面AA1D1D，故①正确；
因为EF∥A1C1，A1C1与平面BC1D1相交，所以EF与平面BC1D1相交，故②错误；
因为E，F，G分别是A1B1，B1C1，BB1的中点，
所以FG∥BC1，因为FG⊄平面BC1D1，BC1⊂平面BC1D1，
所以FG∥平面BC1D1，故③正确；
因为EF与平面BC1D1相交，所以平面EFG与平面BC1D1相交，故④错误．故选A．
6.如图，正方体ABCD­A1B1C1D1中，AB＝2，点E为AD的中点，点F在CD上．若EF∥平面AB1C，则线段EF的长等于________．

解析：因为EF∥平面AB1C，EF⊂平面ABCD，平面ABCD∩平面AB1C＝AC，所以EF∥AC，所以点F为DC的中点．
故EF＝AC＝.
答案：
7．在下面给出的条件中，若条件足够推出a∥α，则在横线上填“OK”；若条件不能保证推出a∥α，则请在横线上补足条件：
(1)条件：a∥b，b∥c，c⊂α，______，结论：a∥α；
(2)条件：α∩β＝b，a∥b，a⊂β，______，结论：a∥α.
解析：因为a∥b，b∥c，c⊂α，所以由直线与平面平行的判定定理得，当a⊄α时，a∥α.因为α∩β＝b，a∥b，a⊂β，则由直线与平面平行的判定定理得a∥α.
答案：a⊄α　OK
8．在四面体A­BCD中，M，N分别是△ACD，△BCD的重心，则四面体的四个面中与MN平行的是________．
解析：如图，取CD的中点E，连接AE，BE，

则EM∶MA＝1∶2，EN∶BN＝1∶2，
所以MN∥AB.
因为AB⊂平面ABD，MN⊄平面ABD，AB⊂平面ABC，MN⊄平面ABC，
所以MN∥平面ABD，MN∥平面ABC.
答案：平面ABD与平面ABC
9.在如图所示的一块木料中，棱BC平行于平面A′B′C′D′.

(1)要经过平面A′B′C′D′内的一点P和棱BC将木料锯开，应怎样画线？
(2)所画的线与平面ABCD是什么位置关系？并证明你的结论．
解： (1)过点P作B′C′的平行线，

交A′B′，C′D′于点E，F，
连接BE，CF.
作图如右：
(2)EF∥平面ABCD.理由如下：
因为BC∥平面A′B′C′D′，
又因为平面B′C′CB∩平面A′B′C′D′＝B′C′，
所以BC∥B′C′，因为EF∥B′C′，所以EF∥BC，
又因为EF⊄平面ABCD，BC⊂平面ABCD，
所以EF∥平面ABCD.
10．(2020·南昌市摸底调研)如图，在四棱锥P­ABCD中，∠ABC＝∠ACD＝90°，∠BAC＝∠CAD＝60°，PA⊥平面ABCD，PA＝2，AB＝1.设M，N分别为PD，AD的中点．

(1)求证：平面CMN∥平面PAB；
(2)求三棱锥P­ABM的体积．
解：(1)证明：因为M，N分别为PD，AD的中点，
所以MN∥PA，
又MN⊄平面PAB，PA⊂平面PAB，
所以MN∥平面PAB.
在Rt△ACD中，∠CAD＝60°，CN＝AN，
所以∠ACN＝60°.
又∠BAC＝60°，
所以CN∥AB.
因为CN⊄平面PAB，AB⊂平面PAB，
所以CN∥平面PAB.
又CN∩MN＝N，所以平面CMN∥平面PAB.
(2)由(1)知，平面CMN∥平面PAB，
所以点M到平面PAB的距离等于点C到平面PAB的距离．
因为AB＝1，∠ABC＝90°，∠BAC＝60°，所以BC＝，
所以三棱锥P­ABM的体积V＝VM­PAB＝VC­PAB＝VP­ABC＝××1××2＝.
[综合题组练]
1．如图，在四面体ABCD中，若截面PQMN是正方形，则在下列说法中，错误的为(　　)

A．AC⊥BD
B．AC＝BD
C．AC∥截面PQMN
D．异面直线PM与BD所成的角为45°
解析：选B．因为截面PQMN是正方形，
所以PQ∥MN，QM∥PN，
则PQ∥平面ACD，QM∥平面BDA，
所以PQ∥AC，QM∥BD，
由PQ⊥QM可得AC⊥BD，故A正确；
由PQ∥AC可得AC∥截面PQMN，故C正确；
由BD∥PN，
所以∠MPN是异面直线PM与BD所成的角，且为45°，D正确；
由上面可知：BD∥PN，MN∥AC.
所以＝，＝，
而AN≠DN，PN＝MN，
所以BD≠AC.B错误．故选B．
2．如图，透明塑料制成的长方体容器ABCD­A1B1C1D1内灌进一些水，固定容器底面一边BC于地面上，再将容器倾斜，随着倾斜度的不同，有下面四个命题：

①没有水的部分始终呈棱柱形；②水面EFGH所在四边形的面积为定值；③棱A1D1始终与水面所在的平面平行；④当容器倾斜如图所示时，BE·BF是定值．
其中正确的个数是(　　)
A．1 B．2
C．3 D．4
解析：选C．由题图，显然①是正确的，②是错的；
对于③因为A1D1∥BC，BC∥FG，
所以A1D1∥FG且A1D1⊄平面EFGH，
所以A1D1∥平面EFGH(水面)．
所以③是正确的；
因为水是定量的(定体积V)．
所以S△BEF·BC＝V，
即BE·BF·BC＝V.
所以BE·BF＝(定值)，
即④是正确的，故选C．
3.如图，在正方体ABCD­A1B1C1D1中判断下列位置关系：

(1)AD1所在的直线与平面BCC1的位置关系是______；
(2)平面A1BC1与平面ABCD的位置关系是______．
解析：(1)AD1所在直线与平面BCC1的位置关系是平行．理由：AB∥C1D1，且AB＝C1D1，可得四边形ABC1D1为平行四边形，即有AD1∥BC1，AD1⊄平面BCC1，BC1⊂平面BCC1，则AD1∥平面BCC1.

(2)平面A1BC1与平面ABCD的位置关系是相交．理由：平面A1BC1与平面ABCD有一个交点B，由公理3得，如果两个平面有一个公共点，那么它们还有其他公共点，这些公共点在一条直线上，这条直线为交线．如图，过点B作AC的平行线l，即为交线．
答案：平行　相交
4．在正四棱柱ABCD­A1B1C1D1中，O为底面ABCD的中心，P是DD1的中点，设Q是CC1上的点，则点Q满足条件________时，有平面D1BQ∥平面PAO.
解析：如图所示，设Q为CC1的中点，因为P为DD1的中点，所以QB∥PA.连接DB，因为P，O分别是DD1，DB的中点，所以D1B∥PO，又D1B⊄平面PAO，QB⊄平面PAO，PO⊂平面PAO，PA⊂平面PAO，所以D1B∥平面PAO，QB∥平面PAO，又D1B∩QB＝B，所以平面D1BQ∥平面PAO.故Q为CC1的中点时，有平面D1BQ∥平面PAO.

答案：Q为CC1的中点
5．如图，四边形ABCD与ADEF为平行四边形，M，N，G分别是AB，AD，EF的中点．

(1)求证：BE∥平面DMF；
(2)求证：平面BDE∥平面MNG.
证明：(1)如图，连接AE，则AE必过DF与GN的交点O，连接MO，则MO为△ABE的中位线，所以BE∥MO，又BE⊄平面DMF，MO⊂平面DMF，所以BE∥平面DMF.

(2)因为N，G分别为平行四边形ADEF的边AD，EF的中点，所以DE∥GN，又DE⊄平面MNG，GN⊂平面MNG，
所以DE∥平面MNG.
又M为AB的中点，
所以MN为△ABD的中位线，
所以BD∥MN，又BD⊄平面MNG，MN⊂平面MNG，
所以BD∥平面MNG，
又DE与BD为平面BDE内的两条相交直线，所以平面BDE∥平面MNG.
6. (2020·南昌二模)如图，四棱锥P­ABCD中，底面ABCD是直角梯形，AB∥CD，AB⊥AD，AB＝2CD＝2AD＝4，侧面PAB是等腰直角三角形，PA＝PB，平面PAB⊥平面ABCD，点E，F分别是棱AB，PB上的点，平面CEF∥平面PAD.

(1)确定点E，F的位置，并说明理由；
(2)求三棱锥F­DCE的体积．
解：(1)因为平面CEF∥平面PAD，平面CEF∩平面ABCD＝CE，
平面PAD∩平面ABCD＝AD，
所以CE∥AD，又AB∥DC，
所以四边形AECD是平行四边形，
所以DC＝AE＝AB，
即点E是AB的中点．
因为平面CEF∥平面PAD，平面CEF∩平面PAB＝EF，
平面PAD∩平面PAB＝PA，
所以EF∥PA，又点E是AB的中点，
所以点F是PB的中点．
综上，E，F分别是AB，PB的中点．
(2)连接PE，由题意及(1)知PA＝PB，AE＝EB，
所以PE⊥AB，又平面PAB⊥平面ABCD，平面PAB∩平面ABCD＝AB，
所以PE⊥平面ABCD.
又AB∥CD，AB⊥AD，
所以VF­DEC＝VP­DEC＝S△DEC×PE＝××2×2×2＝.