陕西省咸阳市秦都区西北工大启迪中学2022-2023学年八年级上学期第一次月考数学试卷（含答案）

2022-2023学年陕西省咸阳市秦都区西北工大启迪中学八年级（上）第一次月考数学试卷

一、选择题（共10小题，每小题3分，计30分）

1．（3分）的相反数为　　

A． B． C．3 D．

2．（3分）在下列各数中，是无理数的是　　

A． B． C． D．

3．（3分）下列式子不是二次根式的是　　

A． B． C． D．

4．（3分）通过估算，估计的值应在　　

A．之间 B．之间 C．之间 D．之间

5．（3分）在下列各式中正确的是　　

A． B． C． D．

6．（3分）的三条边分别为，，，下列条件不能判断是直角三角形的是　　

A． B． 

C． D．，，

7．（3分）下列说法：①无限小数都是无理数；②无理数都是带根号的数；③负数没有立方根；④的平方根是；⑤无理数减去任意一个有理数仍为无理数．其中正确的有　　

A．0个 B．1个 C．2个 D．3个

8．（3分）底边上的高为4，且底边长为12的等腰三角形周长为　　

A． B． C． D．

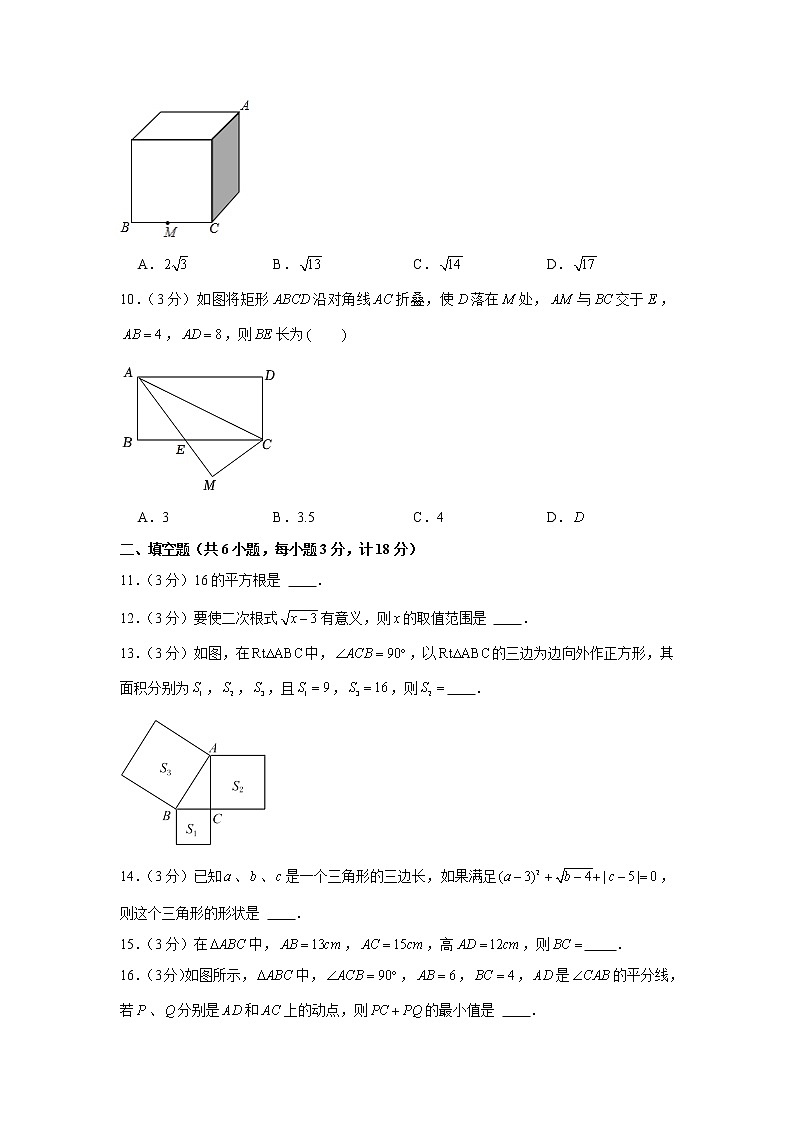
9．（3分）如图，正方体盒子棱长为2，为的中点，一只蚂蚁从点沿盒子的表面爬行到点的最短距离为　　

A． B． C． D．

10．（3分）如图将矩形沿对角线折叠，使落在处，与交于，，，则长为　　

A．3 B．3.5 C．4 D．

二、填空题（共6小题，每小题3分，计18分）

11．（3分）16的平方根是 　　．

12．（3分）要使二次根式有意义，则的取值范围是 　　．

13．（3分）如图，在中，，以的三边为边向外作正方形，其面积分别为，，，且，，则　　．

14．（3分）已知、、是一个三角形的三边长，如果满足，则这个三角形的形状是 　　．

15．（3分）在中，，，高，则　 　．

16．（3分）如图所示，中，，，，是的平分线，若、分别是和上的动点，则的最小值是 　　．

三、解答题（共7道题，共52分）

17．（6分）求下列式子中的的值：

（1）；

（2）．

18．（12分）计算：

（1）；

（2）；

（3）；

（4）．

19．（5分）请在数轴上用尺规作出的对应的点．

20．（6分）已知一个正数的平方根分别是和，的立方根为．

（1）求的算术平方根；

（2）若是的整数部分，求的平方根．

21．（6分）已知：如图，四边形中，，，，，，求四边形的面积．

22．（7分）小渝和小川是一对好朋友，如图，小渝家住，小川家住．两家相距10公里，小渝家在一条笔直的公路边上，小川家到这条公路的距离为6公里，两人相约在公路处见面，且两家到见面地点的距离相等，求小渝家到见面地点的距离．

23．（10分）在中，，分别以、为边向外作正方形和正方形．

（1）当时，正方形的周长　　（用含的代数式表示）；

（2）连接．试说明：三角形的面积等于正方形面积的一半；

（3）已知，且点是线段上的动点，点是线段上的动点，当点和点在移动过程中，的周长是否存在最小值？若存在，求出这个最小值；若不存在，请说明理由．

2022-2023学年陕西省咸阳市秦都区西北工大启迪中学八年级（上）第一次月考数学试卷

参考答案与试题解析

一、选择题（共10小题，每小题3分，计30分）

1．（3分）的相反数为　　

A． B． C．3 D．

【分析】根据相反数的定义求解即可．

【解答】解：的相反数为，

故选：．

2．（3分）在下列各数中，是无理数的是　　

A． B． C． D．

【分析】无理数就是无限不循环小数．理解无理数的概念，一定要同时理解有理数的概念，有理数是整数与分数的统称．即有限小数和无限循环小数是有理数，而无限不循环小数是无理数．由此即可判定选择项．

【解答】解：．，是整数，属于有理数，故本选项不符合题意；

．是分数，属于有理数，故本选项不符合题意；

．，是整数，属于有理数，故本选项不符合题意；

．是无理数，，故本选项符合题意．

故选：．

3．（3分）下列式子不是二次根式的是　　

A． B． C． D．

【分析】形如的式子是二次根式，依据定义即可判断．

【解答】解：、是二次根式，故本选项不符合题意；

、是二次根式，故本选项不符合题意；

、是二次根式，故本选项不符合题意；

、不是根式，故本选项符合题意．

故选：．

4．（3分）通过估算，估计的值应在　　

A．之间 B．之间 C．之间 D．之间

【分析】依据被开方数越大对应的算术平方根越大进行比较即可．

【解答】解：，

，

．

故选：．

5．（3分）在下列各式中正确的是　　

A． B． C． D．

【分析】根据二次根式的性质即可求解．

【解答】解：．，则选项不符合题意；

．，则选项不符合题意；

．，则选项不符合题意；

．，则选项符合题意；

故选：．

6．（3分）的三条边分别为，，，下列条件不能判断是直角三角形的是　　

A． B． 

C． D．，，

【分析】根据勾股定理的逆定理及三角形内角和定理对各选项进行逐一判断即可．

【解答】解：、，

，

，

此三角形是直角三角形，故本选项不符合题意；

、，，

，

此三角形是直角三角形，故本选项不符合题意；

、设，则，，

，

，解得，

，

此三角形不是直角三角形，故本选项符合题意；

、，

此三角形是直角三角形，故本选项不符合题意；

故选：．

7．（3分）下列说法：①无限小数都是无理数；②无理数都是带根号的数；③负数没有立方根；④的平方根是；⑤无理数减去任意一个有理数仍为无理数．其中正确的有　　

A．0个 B．1个 C．2个 D．3个

【分析】根据无理数，立方根，平方根的意义，逐一判断即可解答．

【解答】解：①无限不循环小数都是无理数，故①不正确；

②无理数不一定是带根号的数，例如：是有理数，故②不正确；

③负数有立方根，故③不正确；

④的平方根是，故④不正确；

⑤无理数减去任意一个有理数仍为无理数，故⑤正确；

所以，上列说法中正确的有1个，

故选：．

8．（3分）底边上的高为4，且底边长为12的等腰三角形周长为　　

A． B． C． D．

【分析】作，使，于点，，，则，，即可根据勾股定理求得，再求出该三角形的周长．

【解答】解：如图，中，，于点，，，

，

，

，

，

该等腰三角形的周长为，

故选：．

9．（3分）如图，正方体盒子棱长为2，为的中点，一只蚂蚁从点沿盒子的表面爬行到点的最短距离为　　

A． B． C． D．

【分析】把此正方体的点所在的面展开，然后在平面内，利用勾股定理求点和点间的线段长，即可得到蚂蚁爬行的最短距离．在直角三角形中，一条直角边长等于2，另一条直角边长等于3，利用勾股定理可求得．

【解答】解：将正方体展开，连接，

根据两点之间线段最短，．

答：蚂蚁从点爬行到点的最短距离为．

故选：．

10．（3分）如图将矩形沿对角线折叠，使落在处，与交于，，，则长为　　

A．3 B．3.5 C．4 D．

【分析】根据翻折变换和矩形的性质，得出，在直角三角形中由勾股定理列方程求解即可．

【解答】解：由翻折变换可知，，

四边形是矩形，

，

，

，

，

设，则，

在中，由勾股定理得，

，

即，

解得，

即，

故选：．

二、填空题（共6小题，每小题3分，计18分）

11．（3分）16的平方根是 　　．

【分析】根据平方根的定义，求数的平方根，也就是求一个数，使得，则就是的平方根，由此即可解决问题．

【解答】解：，

的平方根是．

故答案为：．

12．（3分）要使二次根式有意义，则的取值范围是 　　．

【分析】直接利用二次根式的定义得出答案．

【解答】解：二次根式有意义，故，

则的取值范围是：．

故答案为：．

13．（3分）如图，在中，，以的三边为边向外作正方形，其面积分别为，，，且，，则　7　．

【分析】根据勾股定理得，，再利用正方形的面积公式可得答案．

【解答】解：在中，由勾股定理得，，

，

，，

，

故答案为：7．

14．（3分）已知、、是一个三角形的三边长，如果满足，则这个三角形的形状是 　直角三角形　．

【分析】首先根据绝对值，平方数与算术平方根的非负性，求出，，的值，再根据勾股定理的逆定理判断其形状是直角三角形．

【解答】解：，，，，

，，，

解得：，，，

，

这个三角形的形状是直角三角形．

故答案为：直角三角形．

15．（3分）在中，，，高，则　或　．

【分析】高线可能在三角形的内部也可能在三角形的外部，本题应分两种情况进行讨论．分别依据勾股定理即可求解．

【解答】解：由于高的位置是不确定的，所以应分情况进行讨论．

（1）为锐角三角形，高在内部．，

，．

（2）为钝角三角形，高在外部．方法同（1）可得到，，．

16．（3分）如图所示，中，，，，是的平分线，若、分别是和上的动点，则的最小值是 　　．

【分析】如图作于交于点，作此时最短，利用面积法求出即可解决问题．

【解答】解：如图，作于交于点，作此时最短．

，，平分，

，

此时最短（垂线段最短）．

在中，，，，

，

，

．

的最小值为．

故答案为：．

三、解答题（共7道题，共52分）

17．（6分）求下列式子中的的值：

（1）；

（2）．

【分析】（1）先移项，然后根据直接开平方法可以解答此方程；

（2）先变形，然后根据立方根的定义即可解答此方程．

【解答】解：（1），

，

，

解得，；

（2），

，

，

．

18．（12分）计算：

（1）；

（2）；

（3）；

（4）．

【分析】（1）先化简二次根式，然后合并同类二次根式即可；

（2）根据二次根式的混合运算的法则计算即可；

（3）先化简绝对值和负指数，然后根据混合运算的法则计算即可；

（4）根据平方差和完全平方公式计算即可．

【解答】解：（1）

；

（2）

；

（3）

；

（4）

．

19．（5分）请在数轴上用尺规作出的对应的点．

【分析】过所在的点作且，连接，则，以为圆心，为半径作弧交数轴于点，即为所求．

【解答】解：如图：即为所求．

20．（6分）已知一个正数的平方根分别是和，的立方根为．

（1）求的算术平方根；

（2）若是的整数部分，求的平方根．

【分析】（1）根据平方根与立方根的意义可得，，从而求出，，然后代入式子中进行计算即可解答；

（2）先估算出的值的范围，从而求出的值，然后代入式子中进行计算即可解答．

【解答】解：（1）由题意得：

，，

解得：，，

，

的算术平方根是；

（2），

，

的整数部分是3，

，

，

的平方根是．

21．（6分）已知：如图，四边形中，，，，，，求四边形的面积．

【分析】先根据勾股定理求出的长度，再根据勾股定理的逆定理判断出的形状，再利用三角形的面积公式求解即可．

【解答】解：，

，

在中，，

，，

，

为直角三角形，

．

故四边形的面积为．

22．（7分）小渝和小川是一对好朋友，如图，小渝家住，小川家住．两家相距10公里，小渝家在一条笔直的公路边上，小川家到这条公路的距离为6公里，两人相约在公路处见面，且两家到见面地点的距离相等，求小渝家到见面地点的距离．

【分析】根据勾股定理得出的长度，进而解答即可．

【解答】解：由题意知，，公里，公里，

由勾股定理得：（公里），

，

设为公里，则，，

解得：，

即公里，

即小渝家到见面地点的距离为6.25公里．

23．（10分）在中，，分别以、为边向外作正方形和正方形．

（1）当时，正方形的周长　　（用含的代数式表示）；

（2）连接．试说明：三角形的面积等于正方形面积的一半；

（3）已知，且点是线段上的动点，点是线段上的动点，当点和点在移动过程中，的周长是否存在最小值？若存在，求出这个最小值；若不存在，请说明理由．

【分析】（1）直接由正方形的性质得出答案即可；

（2）连接，证明，利用的面积的面积得出结论；

（3）作点关于的对称点，点关于的对称点，利用对称的性质得出的周长的最小值为，进一步求得问题即可．

【解答】解：（1）四边形是正方形，

，

当时，正方形的周长为，

故答案为：；

（2）如图1，连接，

在和中，

，

的面积的面积正方形的面积；

（3）的周长存在最小值．

如图2，作点关于的对称点，

点关于的对称点，

，

的周长的最小值为，

过作交的延长线于，

△为等腰直角三角形，

，

，

，，

的周长的最小值为．