江苏省兴化市楚水实验学校2022-2023学年八年级上学期第一次阶段达标评价数学试卷（含答案）

2022—2023学年度第一学期第一次阶段达标评价

八年级    数学

考试时间：120分钟       分值：150分      命题人：

卷首说明：

1. 答题前，考生务必将本人的学校、班级、姓名、考试号规范填写（填涂）在答题纸相应的位置上。
2. 考生答题答题必须用0.5毫米黑色墨水签字笔，写在“答题纸” 指定位置处，答在试卷、草稿纸等其他位置上一律无效。

第一部分   选择题（共18分）

一、选择题（本大题共6小题，每小题3分，共18分.在每小题所给出的四个选项中，恰有一项是符合题目要求的）

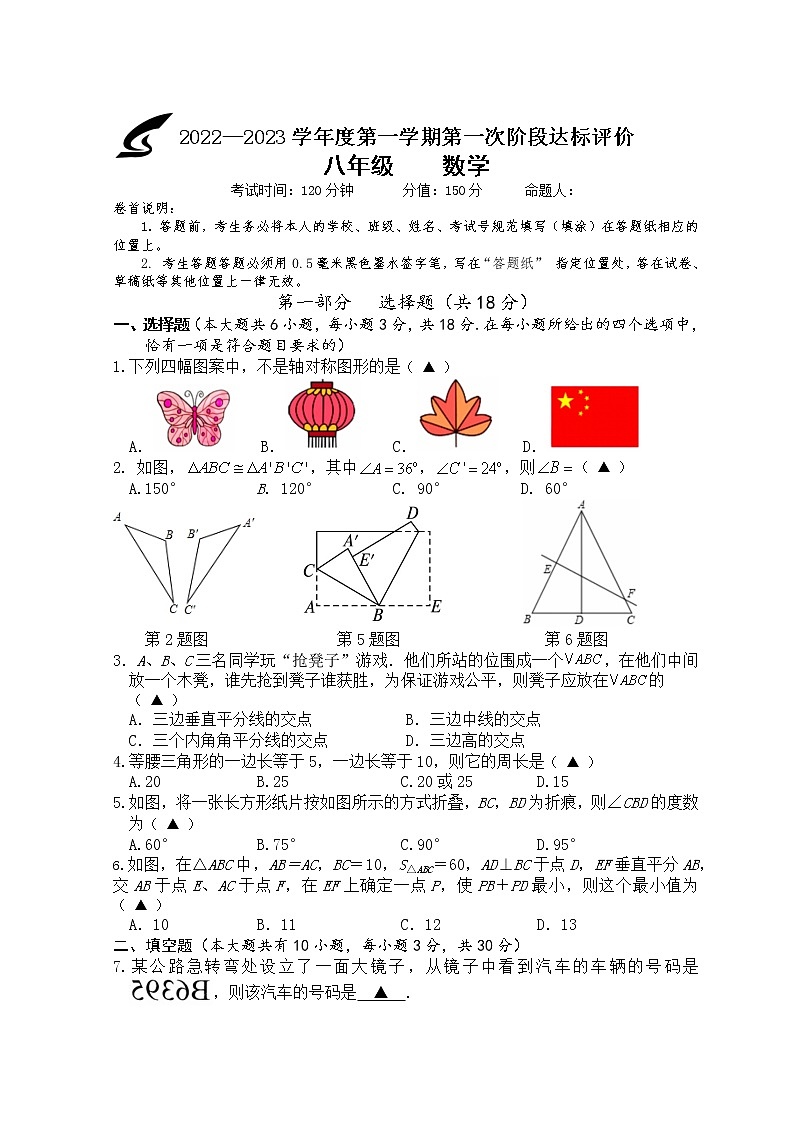
1.下列四幅图案中，不是轴对称图形的是（ ▲ ）

A．   B．    C．   D．

2. 如图，，其中，，则（ ▲ ）

A.150°         B. 120°         C. 90°         D. 60°                 

    第2题图                第5题图                  第6题图

3．A、B、C三名同学玩“抢凳子”游戏．他们所站的位围成一个，在他们中间放一个木凳，谁先抢到凳子谁获胜，为保证游戏公平，则凳子应放在的（ ▲ ）

A．三边垂直平分线的交点   B．三边中线的交点

C．三个内角角平分线的交点   D．三边高的交点

4.等腰三角形的一边长等于5，一边长等于10，则它的周长是（ ▲ ）

A.20            B.25              C.20或25        D.15

5.如图，将一张长方形纸片按如图所示的方式折叠，BC，BD为折痕，则∠CBD的度数为（ ▲ ）

A.60°      B.75°            C.90°        D.95°

6.如图，在△ABC中，AB＝AC，BC＝10，S△ABC＝60，AD⊥BC于点D，EF垂直平分AB，交AB于点E、AC于点F，在EF上确定一点P，使PB＋PD最小，则这个最小值为（ ▲ ）

A．10           B．11             C．12            D．13

二、填空题（本大题共有10小题，每小题3分，共30分）

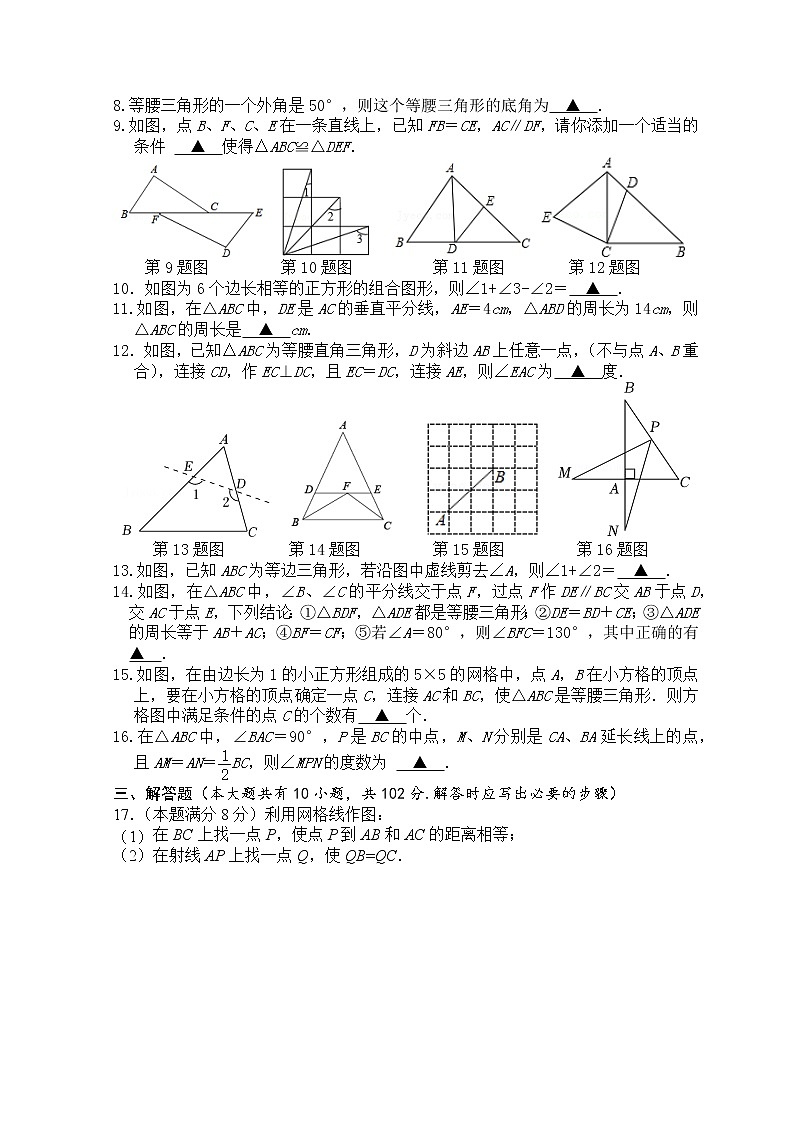
7.某公路急转弯处设立了一面大镜子，从镜子中看到汽车的车辆的号码是，则该汽车的号码是　▲　．

8.等腰三角形的一个外角是50°，则这个等腰三角形的底角为　▲　．

9.如图，点B、F、C、E在一条直线上，已知FB＝CE，AC∥DF，请你添加一个适当的条件 　▲　使得△ABC≌△DEF．

    第9题图         第10题图          第11题图        第12题图

10．如图为6个边长相等的正方形的组合图形，则∠1+∠3-∠2＝　▲　．

11.如图，在△ABC中，DE是AC的垂直平分线，AE＝4cm，△ABD的周长为14cm，则△ABC的周长是　▲　cm．

12．如图，已知△ABC为等腰直角三角形，D为斜边AB上任意一点，（不与点A、B重合），连接CD，作EC⊥DC，且EC＝DC，连接AE，则∠EAC为　▲　度．

     第13题图        第14题图         第15题图         第16题图   

13.如图，已知ABC为等边三角形，若沿图中虚线剪去∠A，则∠1+∠2＝　▲　．

14.如图，在△ABC中，∠B、∠C的平分线交于点F，过点F作DE∥BC交AB于点D，交AC于点E，下列结论：①△BDF，△ADE都是等腰三角形；②DE＝BD＋CE；③△ADE的周长等于AB＋AC；④BF＝CF；⑤若∠A＝80°，则∠BFC＝130°，其中正确的有　▲　．

15.如图，在由边长为1的小正方形组成的5×5的网格中，点A，B在小方格的顶点上，要在小方格的顶点确定一点C，连接AC和BC，使△ABC是等腰三角形．则方格图中满足条件的点C的个数有　▲　个．

16.在△ABC中，∠BAC＝90°，P是BC的中点，M、N分别是CA、BA延长线上的点，且AM＝AN＝BC，则∠MPN的度数为 　▲　．

三、解答题（本大题共有10小题，共102分.解答时应写出必要的步骤）

17．（本题满分8分）利用网格线作图：

（1）在BC上找一点P，使点P到AB和AC的距离相等；

（2）在射线AP上找一点Q，使QB=QC．

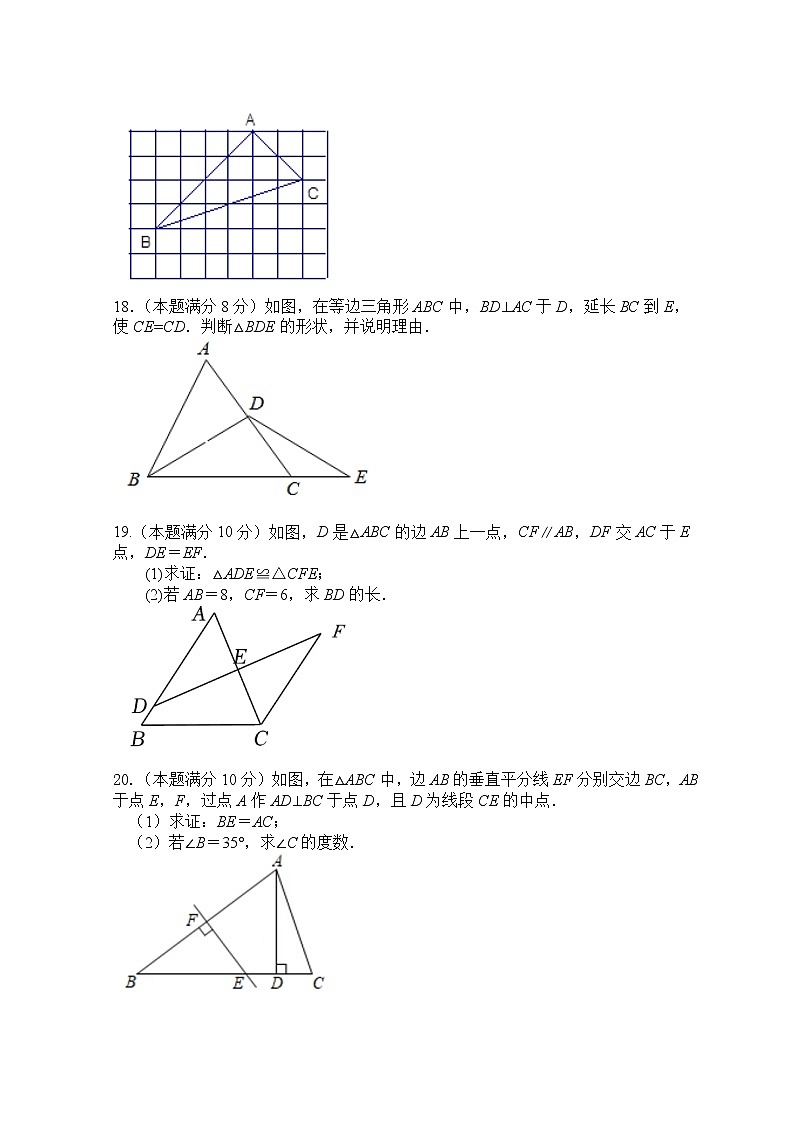
18．（本题满分8分）如图，在等边三角形ABC中，BD⊥AC于D，延长BC到E，使CE=CD．判断△BDE的形状，并说明理由．

19.（本题满分10分）如图，D是△ABC的边AB上一点，CF∥AB，DF交AC于E点，DE＝EF．

(1)求证：△ADE≌△CFE；

(2)若AB＝8，CF＝6，求BD的长．

20.（本题满分10分）如图，在△ABC中，边AB的垂直平分线EF分别交边BC，AB于点E，F，过点A作AD⊥BC于点D，且D为线段CE的中点．

（1）求证：BE＝AC；

（2）若∠B＝35°，求∠C的度数．

21．（本题满分10分）△ABC的三边长分别为m﹣2，2m+1，8．

（1）求m的取值范围；

（2）若△ABC是等腰三角形，求三边长.

22.（本题满分10分）如图，在四边形ABCD中，∠BAD＝∠BCD＝90°，O为BD的中点．

（1）证明∠OAC=∠OCA

（2）若P为AC中点，试判断OP与AC的位置关系．

23.（本题满分10分）在等腰直角△ABC中，AC=BC,∠C=90°.

(1)     请利用尺规在AC边上作一点D,使得点D到AB的距离等于DC

(2)     证明:  DC+BC=AB

24.（本题满分10分）如图所示，已知AE⊥AB，AF⊥AC，AE＝AB，AF＝AC，CE交BA于点D，CE交BF于点M．

求证：(1)EC＝BF；

(2 )EC⊥BF．

25．（本题满分12分）如图，在 △ABC 中，AB=AC=2，∠B=40°，点 D 在线段BC 上运动（D 不与 B，C 重合），连接 AD，作 ∠ADE=40°，DE 与 AC 交于E．

（1）当 ∠BDA=115°时，∠BAD=      °，∠DEC=      °；当点D 从B 向C 运动时，∠BDA 逐渐变    （填“大”或“小”）；

（2）当DC 等于多少时，△ABD 与 △DCE 全等？请说明理由；

（3）在点D 的运动过程中，△ADE 的形状可以是等腰三角形吗？若可以，请直接写出 ∠BDA 的度数；若不可以，请说明理由．

26．（本题满分14分）在等边△ABC的两边AB、AC所在直线上分别有两点M、N，D为△ABC外一点，且∠MDN＝60°，∠BDC＝120°，BD＝DC．探究：当M、N分别在直线AB、AC上移动时，BM、NC、MN之间的数量关系及△AMN的周长Q与等边△ABC的周长L的关系．

（1）如图1，当点M、N在边AB、AC上，且DM＝DN时，BM、NC、MN之间的数量关系是 　   　；此时＝　   　；

（2）如图2，点M、N在边AB、AC上，且当DM≠DN时，猜想（I）问的两个结论还成立吗？若成立请直接写出你的结论；若不成立请说明理由．

（3）如图3，当M、N分别在边AB、CA的延长线上时，探索BM、NC、MN之间的数量关系如何？并给出证明．

2022—2023学年度第一学期第一次阶段达标评价

八年级数学答案

一、选择题

1.D   2.B  3.A   4.B   5.C   6.C

二、填空题

7.B6395    8.130°或25°  9.∠B=∠E（答案不唯一） 10.45°  11.22cm

12.45°    13.240°        14.②③            15.6     16.45°

二、解答题

三、17．【解答】解：（1）如图所示：AP即为所求；

（2）如图所示：Q即为所求．

18．【解答】解：（1）△BDE为等腰三角形．理由如下：

∵△ABC为等边三角形，

∴∠ABC＝∠ACB＝60°，

∵BD⊥AC，

∴∠CBD＝∠ABC＝30°，

∵CD＝CE，

∴∠CDE＝∠E，

而∠CDE+∠E＝∠ACB＝60°，

∴∠E＝30°，

∴∠CBD＝∠E，

∴△BDE为等腰三角形．

19．【解答】（1）证明：如图，∵CF∥AB，

∴∠ADE＝∠F，∠A＝∠ECF，

在△ADE和△CFE中，

，

∴△ADE≌△CFE（AAS）．

（2）解：∵AD＝CF＝6，AB＝8，

∴BD＝AB﹣AD＝2，

∴BD的长是2．

20．【解答】（1）证明：连接AE，

∵AD⊥BC于点D，且D为线段CE的中点，

∴AD垂直平分CE，

∴AC＝AE，

∵EF垂直平分AB，

∴AE＝BE，

∴BE＝AC；

（2）∠C=70°，

21．【解答】解：（1）根据三角形的三边关系得

，

解得3＜m＜5；

（2）当m﹣2＝2m+1时，

解得m＝﹣3（不合题意，舍去），

当m﹣2＝8时，

解得，m＝10＞5（不合题意，舍去），

当2m+1＝8时，

解得，m＝，

所以若△ABC为等腰三角形，m＝，

则m﹣2＝，2m+1＝8，

所以，△ABC三边长为、8、8．

22．【解答】解：（1）∠OAC＝∠OCA，

理由：∵△ABD是直角三角形，O为BD的中点，

∴OA＝BD，

∵△BDC是直角三角形，O为BD的中点，

∴OC＝BD，

∴OA＝OC，

∴∠OAC＝∠OCA；

（2）OP⊥AC，

理由：由（1）知AO＝OC，

∵P为AC中点，

∴OP⊥AC．

23. （1）作∠B的平分线交AC于点D

      (2)作DH⊥AB 通过证明BH=BC △AHD是等腰三角形得AH=DH=DC 即可

24．【解答】证明：（1）∵AE⊥AB，AF⊥AC，

∴∠BAE＝∠CAF＝90°，

∴∠BAE+∠BAC＝∠CAF+∠BAC，

∴∠EAC＝∠BAF，

在△ABF和△AEC中，

，

∴△ABF≌△AEC（SAS），

∴EC＝BF；

（2）如图，由（1）得：△ABF≌△AEC，

∴∠AEC＝∠ABF，

∵AE⊥AB，

∴∠BAE＝90°，

∴∠AEC+∠ADE＝90°，

∴∠BAE＝90°（对顶角相等），

∴∠ABF+∠BDM＝90°，

在△BDM中，∠BMD＝180°﹣∠ABF﹣∠BDM＝180°﹣90°＝90°，

所以EC⊥BF．

25．【解答】解：（1）∵∠B＝40°，∠ADB＝115°，

∴∠BAD＝180°﹣40°﹣115°＝25°；

∵∠ADE＝40°，∠ADB＝115°，

∴∠EDC＝180°﹣∠ADB﹣∠ADE＝180°﹣115°﹣40°＝25°．

∴∠DEC＝180°﹣40°﹣25°＝115°，

当点D从B向C运动时，∠BDA逐渐变小，

故答案为：25，115，小；

（2）当DC＝2时，△ABD≌△DCE，

理由：∵∠C＝40°，

∴∠DEC+∠EDC＝140°，

又∵∠ADE＝40°，

∴∠ADB+∠EDC＝140°，

∴∠ADB＝∠DEC，

又∵AB＝DC＝2，

在△ABD和△DCE中，

，

∴△ABD≌△DCE（AAS）；

（3）当∠BDA的度数为110°或80°时，△ADE的形状是等腰三角形，

∵∠BDA＝110°时，

∴∠ADC＝70°，

∵∠C＝40°，

∴∠DAC＝70°，

∴△ADE的形状是等腰三角形；

∵当∠BDA的度数为80°时，

∴∠ADC＝100°，

∵∠C＝40°，

∴∠DAC＝40°，

∴△ADE的形状是等腰三角形．

26．【解答】解（1）BM、NC、MN之间的数量关系 BM+NC＝MN．

∵DM＝DN，∠MDN＝60°，

∴△MDN是等边三角形，

∵△ABC是等边三角形，

∴∠A＝60°，

∵BD＝CD，∠BDC＝120°，

∴∠BDC＝∠DCB＝30°，

∴∠MBD＝∠NCD＝90°，

在Rt△BDM和Rt△CDN中，

，

∴Rt△BDM≌Rt△CDN，

∴∠BDM＝∠CDN＝30°，BM＝CN，

∴DM＝2BM，DN＝2CN，

∴MN＝2BM＝2CN＝BM+CN，

故答案为：BM+NC＝MN；

（2）猜想：结论仍然成立．

证明：在CN的延长线上截取CM1＝BM，连接DM1．

∵∠MBD＝∠M1CD＝90°，BD＝CD，

∴△DBM≌△DCM1，

∴DM＝DM1，∠MBD＝∠M1CD，M1C＝BM，

∵∠MDN＝60°，∠BDC＝120°，

∴∠M1DN＝∠MDN＝60°，

∴△MDN≌△M1DN，

∴MN＝M1N＝M1C+NC＝BM+NC；

（3）证明：在CN上截取CM1＝BM，连接DM1．

由（2）得，△DBM≌△DCM1，

∴DM＝DM1，

∴∠M1DN＝∠MDN＝60°，

∴△MDN≌△M1DN，

∴MN＝M1N，

∴NC﹣BM＝MN．