
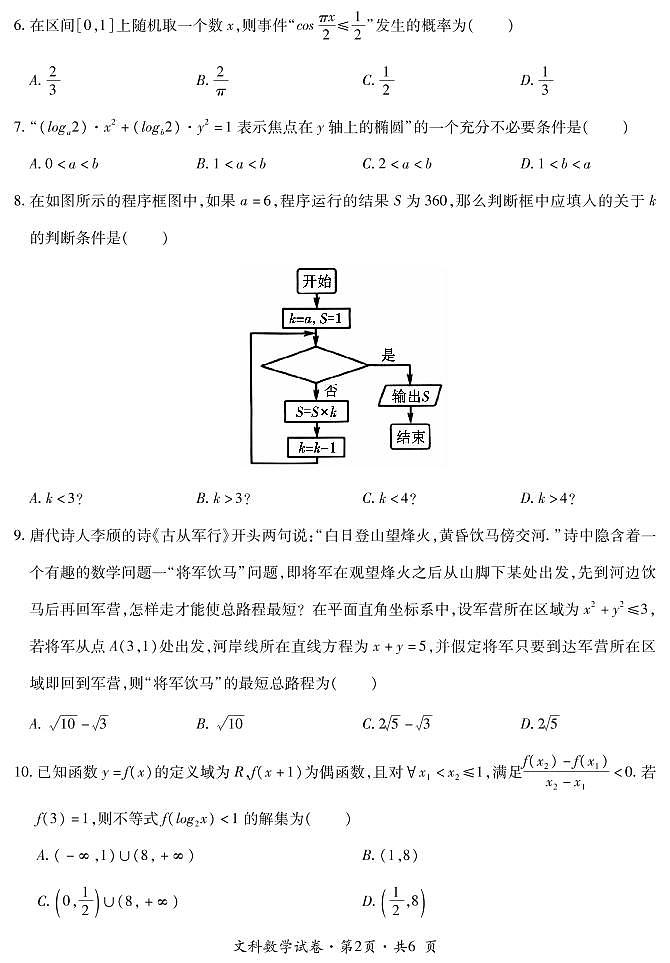
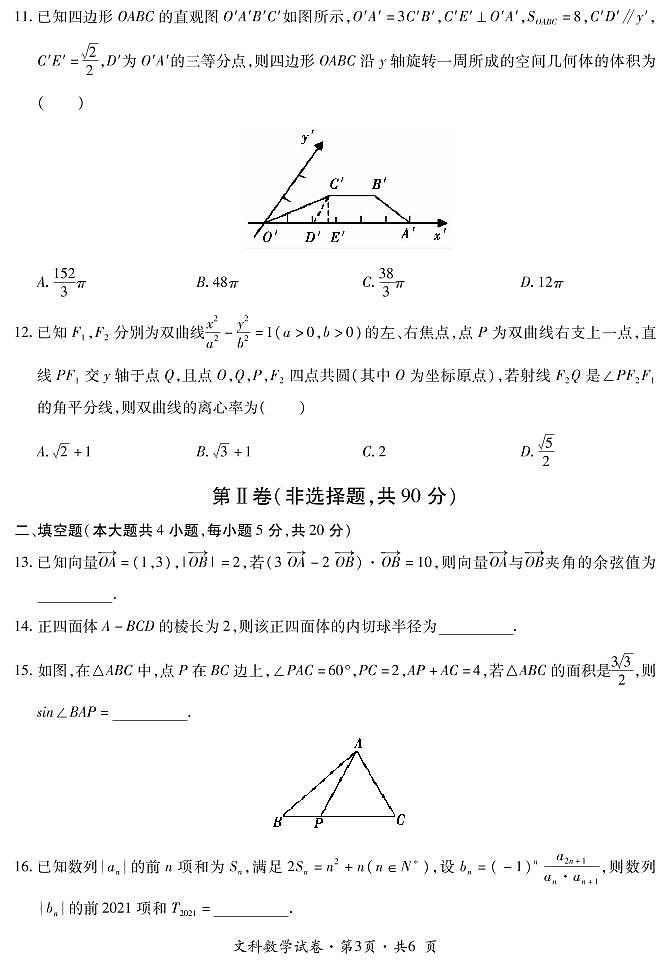



2021曲靖二中高三下学期第二次模拟考试数学(文)试题PDF版含答案
展开2021届高三第二次模拟考试
数 学(文科)参考答案
一、选择题(本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)
DABAC DCACD BB
二、填空题(本大题共4小题,每小题5分,共20分)
13. .
14. .
15. .
16. .
三、解答题(本大题共6小题,共70分.解答应写出文字说明,证明过程或演算步骤)
17.(本小题满分12分)
【解答】(1)证明:方案一:选条件①
当n=1时,2a1=2S1=3a1﹣3﹣4,解得a1=7,
∴a1+2=7+2=9,
当n≥2时,由2Sn=3an﹣3﹣4n,可得
2Sn﹣1=3an﹣1﹣3﹣4(n﹣1),
两式相减,可得
2an=3an﹣3an﹣1﹣4,
即an=3an﹣1+4,
∴an+2=3an﹣1+4+2=3(an﹣1+2),
∴数列{an+2}是以9为首项,3为公比的等比数列,
方案二:选条件②
当n=1时,a1+2=﹣3+2=﹣1,
当n≥2时,an+1+2=﹣an﹣4+2=﹣(an+2),
∴数列{an+2}是以﹣1为首项,﹣1为公比的等比数列, 6分
(2)解:由题意,设等差数列{bn}的公差为d,则
d2,
b1=b3﹣2d=5﹣2×2=1,
∴bn=1+2×(n﹣1)=2n﹣1,n∈N*,
方案一:选条件①
由(1),可得an+2=9•3n﹣1=3n+1,
则cn=(an+2)bn=(2n﹣1)•3n+1,
∴Tn=c1+c2+c3+…+cn=1•32+3•33+5•34+…+(2n﹣1)•3n+1,
3Tn=1•33+3•34+…+(2n﹣3)•3n+1+(2n﹣1)•3n+2,
两式相减,可得
﹣2Tn=1•32+2•33+2•34+…+2•3n+1﹣(2n﹣1)•3n+2
=9+2(2n﹣1)•3n+2
=﹣18﹣2(n﹣1)•3n+2,
∴Tn=(n﹣1)•3n+2+9,n∈N*,
方案二:选条件②
由(1),可得an+2=﹣1•(﹣1)n﹣1=(﹣1)n,
则cn=(an+2)bn=(2n﹣1)•(﹣1)n,
∴Tn=c1+c2+c3+…+cn
=﹣1+3﹣5+…+(2n﹣1)•(﹣1)n,
当n为偶数时,Tn=﹣1+3﹣5+…+(2n﹣1)=2+2+…+2=2n,
当n为奇数时,Tn=﹣1+3﹣5+…﹣(2n﹣1)=2+2+…+2﹣(2n﹣1)=2(2n﹣1)=﹣n,
∴Tn. 12分
18.(本小题满分12分)
【解答】 (1)证明:因为四边形ABB1A1和ACC1A1都是矩形,
所以AA1⊥AB,AA1⊥AC.
因为AB,AC为平面ABC内两条相交直线,
所以AA1⊥平面ABC.
因为直线BC⊂平面ABC,所以AA1⊥BC.
又AC⊥BC,AA1,AC为平面ACC1A1内两条相交直线,
所以BC⊥平面ACC1A1. 5分
(2)取线段AB的中点M,连接A1M,MC,A1C,AC1,设O为A1C,AC1的交点.
由已知可知O为AC1的中点.
连结MD,OE,则MD,OE分别为△ABC,△ACC1的中位线,
所以MD∥AC,MD=AC,OE∥AC,OE=AC因此MD∥OE.
连接OM,从而四边形MDEO为平行四边形,
则DE∥MO.
因为直线DE⊄平面A1MC,MO⊂平面A1MC,
所以直线DE∥平面A1MC,
即线段AB上存在一点M(线段AB的中点),
使直线DE∥平面A1MC. 12分
19.(本小题满分12分)
【解答】解:(1)①由已知得出x与z的关系,如下表:
泡制时间x/min | 0 | 1 | 2 | 3 | 4 |
z | 4.2 | 4.1 | 4.0 | 3.9 | 3.8 |
设线性回归方程,
由题意,得,,
∴(﹣2)×0.2+(﹣1)×0.1+1×(﹣0.1)+2×(﹣0.2)=﹣1,
,
则,
,
则z关于x的线性回归方程为; 5分
②由y=kcx+20(x≥0),得y﹣20=kcx(x≥0),
两边取对数得,ln(y﹣20)=lnk+xlnc,
利用①的结论得:lnc=﹣0.1,lnk=4.2,
∴c=e﹣0.1≈0.9,k=e4.2≈66.7; 8分
(2)由(1)得,y=66.7×0.9x+20(x≥0),
令y=60,得x≈log0.90.6≈4.8.
∴该品种绿茶用85℃的水泡制4.8min后饮用,口感最佳. 12分
20.(本小题满分12分)
【解答】解:(1)设点P的坐标(x,y),
则点P到直线y=3的距离d=|y﹣3|,
过点P做圆x2+(y﹣5)2=16的切线,则切线长|PQ|,
由题意可得|y﹣3|,
整理可得x2=4y,
所以点P的轨迹方程:x2=4y; 5分
(2)证明:设直线AB的方程为:y=kx+b,设A(x1,),B(x2,),
联立直线AB与抛物线的方程:,整理可得:x2﹣4kx﹣4b=0,
则,
由x2=4y可得y,所以y',
所以在A点的切线方程为:y(x﹣x1),
即yx,
同理可得在B点切线方程为yx,
,解得,
由题意可得两条切线的交点R在y=x﹣2上,
所以﹣b=2k﹣2,即b=2﹣2k,
代入直线AB的方程:y=kx+2﹣2k=k(x﹣2)+2,
所以直线AB恒过定点,且定点的坐标为(2,2). 12分
21.(本小题满分12分)
【解答】 (1)∵
∴, 设.
∴,
∴在上为减函数.
∴,
∴
∴函数在上为减函数. 6分
(2)在上恒成立,
在上恒成立,
设,则,
∴,
若显然不满足条件,
若,则时,恒成立,
∴在上为减函数
∴在上恒成立,
∴在上恒成立,
若,则时,,
∴时,
∴在上为增函数,
当时,,
不能使在上恒成立,
∴ 12分
请考生在22、23两题中任选一题作答,如果多做,则按所做的第一题记分.
22.(本小题满分12分)选修4-4:坐标系与参数方程
【解答】解:(1)曲线,
转换为极坐标方程为:.
伸缩变换转换为:代入曲线,
得到极坐标方程为. 5分
(2)把代入,
即:,
转换为,
同理:,
由于,
所以:,
解得:,
故:. 10分
23.(本小题满分10分)选修4-5:不等式选讲
【解答】(1)当时,,
①当时,不等式可化为,解得,∴,
②当时,不等式可化为,解得,∴,
③当时,不等式可化为,解得,∴,
综上可知,原不等式的解集为; 5分
(2)当时,不等式,即,整理得,
则,即,
又,故分离参数可得,
令函数(),显然在上单调递减,∴,
当时,(当且仅当时等号成立),
∴实数的取值范围为。 10分
2021曲靖二中、大理新世纪中学高三第一次模拟考试数学(文)试题PDF版含答案: 这是一份2021曲靖二中、大理新世纪中学高三第一次模拟考试数学(文)试题PDF版含答案,文件包含文科数学答案docx、云南省曲靖市第二中学大理新世纪中学2021届高三第一次模拟考试数学文试题PDF可编辑版pdf、数学文答题卡pdf等3份试卷配套教学资源,其中试卷共18页, 欢迎下载使用。
2021曲靖二中、大理新世纪中学高三第一次模拟考试数学(理)试题PDF版含答案: 这是一份2021曲靖二中、大理新世纪中学高三第一次模拟考试数学(理)试题PDF版含答案
2021曲靖二中、大理新世纪中学高三第一次模拟考试数学(文)试题PDF版含答案: 这是一份2021曲靖二中、大理新世纪中学高三第一次模拟考试数学(文)试题PDF版含答案












