2021莆田锦江中学高二下学期期中考试数学试题含答案

这是一份2021莆田锦江中学高二下学期期中考试数学试题含答案，共9页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
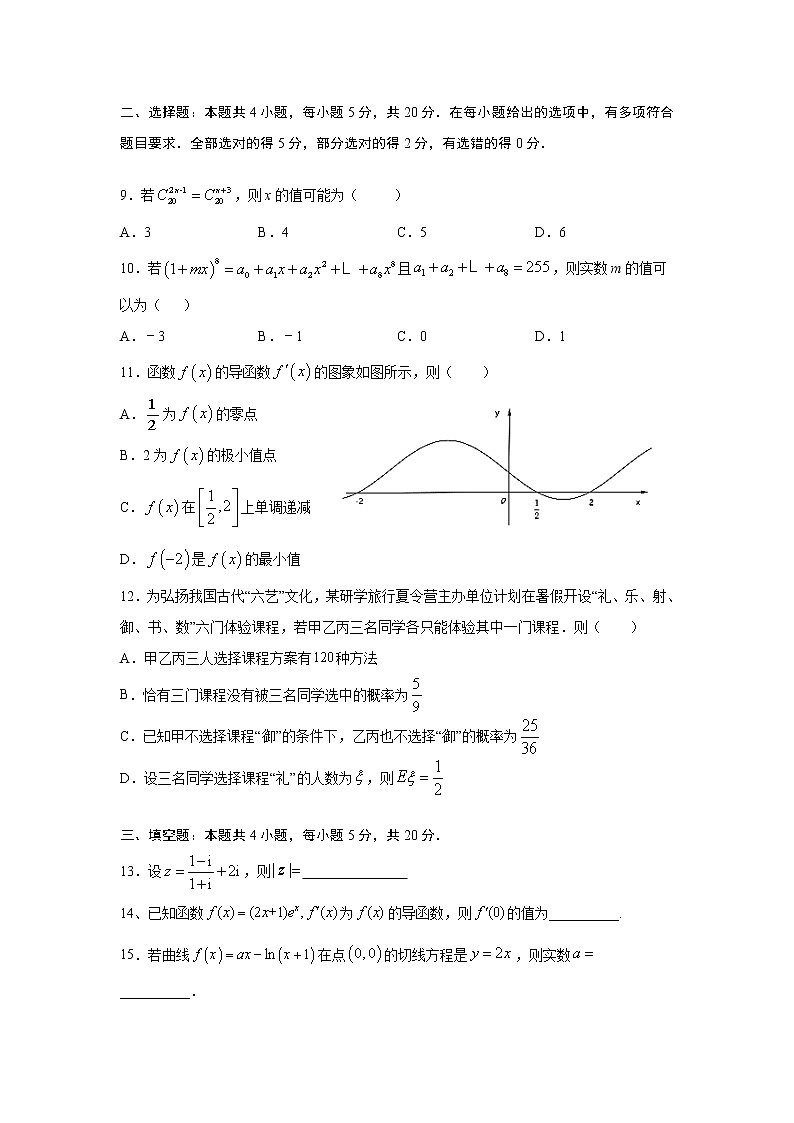
莆田锦江中学2020～2021学年（下）期中质量检测试卷高二数学命题人： 一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中只有一项是符合题目要求的． 1.某班小张等4位同学报名参加A，B，C三个课外活动小组，每位同学限报其中一个小组，且小张不能报A小组，则不同的报名方法有(　　)A． 27种    B． 36种     C． 54种    D． 81种2、若复数，其中i为虚数单位，则 =(　　)A．1+i  B．1−i  C．−1+i  D．−1−i[3、二项式的展开式中的常数项是(　　) A． 第7项    B． 第8项    C． 第9项    D． 第10项 4．已知某一随机变量ξ的分布列如下且Eξ＝6.3，则a的值为(　　)ξ4a9P0.50.1bA．5     B．6       C．7        D．85．某地安排4名工作人员随机分到3个村参加“脱贫攻坚”帮扶活动，且每个人只去一个村，则每个村至少有一名工作人员的概率为(　　)A．    B．    C．    D．6.函数的单调递增区间是 (    )A.      B.(0,3)   C.(1,4)     D.      7、已知a函数f(x)＝x3－12x的极小值点，则a=(　　)A.-4    B. -2      C.4     D.28. 五名同学排成一排照相若甲､乙相邻且乙､丙不相邻，则不同的排法有（    ）A．24种 B．36种 C．48种 D．60种 二、选择题：本题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合题目要求．全部选对的得5分，部分选对的得2分，有选错的得0分． 9．若，则x的值可能为（     ）A．3 B．4 C．5 D．610．若且，则实数m的值可以为（   ）A．﹣3 B．﹣1 C．0 D．111．函数的导函数的图象如图所示，则（    ）A．为的零点B．2为的极小值点C．在上单调递减D．是的最小值12．为弘扬我国古代“六艺”文化，某研学旅行夏令营主办单位计划在暑假开设“礼、乐、射、御、书、数”六门体验课程，若甲乙丙三名同学各只能体验其中一门课程．则（    ）A．甲乙丙三人选择课程方案有种方法B．恰有三门课程没有被三名同学选中的概率为C．已知甲不选择课程“御”的条件下，乙丙也不选择“御”的概率为D．设三名同学选择课程“礼”的人数为，则 三、填空题：本题共4小题，每小题5分，共20分． 13．设，则               14、已知函数为的导函数，则的值为__________.15．若曲线在点的切线方程是，则实数__________．16．某种种子每粒发芽的概率都为0.9，现播种了1000粒，对于没有发芽的种子，每粒需再补种2粒，补种的种子数记为X，则X的数学期望为________．四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．17. 实数m为何值时，复数是：（1）纯虚数；（2）等于；（3）所对应的点在第四象限．   18. ．已知函数的图象在点处的切线斜率为，且时，有极值．（1）求的解析式；（2）求在上的最大值和最小值．   19．一个盒子里有9个大小完全相同的小球，其中4个红球，5个白球，（1）若不放回地从盒中连续取两次球，每次取一个球，求在第一次取到红球的条件下，第二次也取到红球的概率；（2）若从盒中任取三个球，求取出的三个球中，红球的个数的分布列和数学期望．  20. 在一个选拔项目中，每个选手都需要进行四轮考核，每轮设有一个问题，能正确回答者进入下一轮考核，否则被淘汰．已知某选手能正确回答第一、二、三、四轮问题的概率分别为、、、，且各轮问题能否正确回答互不影响．（1）求该选手进入第三轮才被淘汰的概率；（2）求该选手至多进入第三轮考核的概率；（3）该选手在选拔过程中回答过的问题的个数记为，求随机变量的分布列． 21. 2021年3月北京市政府为做好“两会”接待服务工作，对可能遭受污染的某海产品在进入餐饮区前必须进行两轮检测，只有两轮都合格才能进行销售，否则不能销售．已知该海产品第一轮检测不合格的概率为，第二轮检测不合格的概率为，两轮检测是否合格相互没有影响．(1)求该海产品不能销售的概率；(2)如果该海产品可以销售，则每件产品可获利40元；如果该海产品不能销售，则每件产品亏损80元(即获利－80元)．已知一箱中有该海产品4件，记一箱该海产品获利ξ元，求ξ的分布列，并求出数学期望E(ξ)．     22. 已知函数.（1）讨论的单调性；（2）当，若关于的不等式在上恒成立，求实数的取值范围. 
2021高二下数学期中答案 一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中只有一项是符合题目要求的． 1－5 CBCCD    6-8 DDB 二、选择题：本题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合题目要求．全部选对的得5分，部分选对的得2分，有选错的得0分．9.BD      10.AD      11.BC       12.BCD 三、填空题：本题共4小题，每小题5分，共20分． 13．  1    14.   3      15．3   16.  200 四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．17. 实数m为何值时，复数是：（1）纯虚数；（2）等于；（3）所对应的点在第四象限．解：（1）由题意可得，解得.　（2）由复数相等可得，解得.（3）由复数的几何意义可得，解得. 18. ．已知函数的图象在点处的切线斜率为，且时，有极值．（1）求的解析式；（2）求在上的最大值和最小值．解：（1）由题意可得，．由解得经检验得时，有极大值．所以．（2）由（1）知，．令，得，，，的值随的变化情况如下表：2 00  单调递增极大值单调递减极小值单调递增 函数值3 8  8由表可知在上的最大值为8，最小值为． 19．一个盒子里有9个大小完全相同的小球，其中4个红球，5个白球，（1）若不放回地从盒中连续取两次球，每次取一个球，求在第一次取到红球的条件下，第二次也取到红球的概率；（2）若从盒中任取三个球，求取出的三个球中，红球的个数的分布列和数学期望．解：（1）设事件“第一次取到红球”，事件“第二次取到红球”，则，（2）记从盒中任取3个球，取出的3个球中红球的个数为，则服从超几何分布，的可能取值为0、1、2、3，则所以的分布列为：0123 20. 在一个选拔项目中，每个选手都需要进行四轮考核，每轮设有一个问题，能正确回答者进入下一轮考核，否则被淘汰．已知某选手能正确回答第一、二、三、四轮问题的概率分别为、、、，且各轮问题能否正确回答互不影响．（1）求该选手进入第三轮才被淘汰的概率；（2）求该选手至多进入第三轮考核的概率；（3）该选手在选拔过程中回答过的问题的个数记为，求随机变量的分布列．解：设事件表示“该选手能正确回答第轮问题”，由已知，，，．（1）设事件表示“该选手进入第三轮才被淘汰”，则．（2）设事件表示“该选手至多进入第三轮考核”，则．（3）的可能取值为1，2，3，4．，，，，所以的分布列为1234 21.(本小题满分12分)2021年3月北京市政府为做好“两会”接待服务工作，对可能遭受污染的某海产品在进入餐饮区前必须进行两轮检测，只有两轮都合格才能进行销售，否则不能销售．已知该海产品第一轮检测不合格的概率为，第二轮检测不合格的概率为，两轮检测是否合格相互没有影响．(1)求该海产品不能销售的概率；(2)如果该海产品可以销售，则每件产品可获利40元；如果该海产品不能销售，则每件产品亏损80元(即获利－80元)．已知一箱中有该海产品4件，记一箱该海产品获利ξ元，求ξ的分布列，并求出数学期望E(ξ)．解　(1)记“该海产品不能销售”为事件A，则P(A)＝1－×＝.所以，该海产品不能销售的概率为.(2)由已知，可知ξ的可能取值为－320，－200，－80,40,160.P(ξ＝－320)＝4＝，P(ξ＝－200)＝C·3·＝，P(ξ＝－80)＝C·2·2＝，P(ξ＝40)＝C··3＝，P(ξ＝160)＝4＝.所以ξ的分布列为ξ－320－200－8040160PE(ξ)＝－320×－200×－80×＋40×＋160×＝40. 22. 已知函数.（1）讨论的单调性；（2）当，若关于的不等式在上恒成立，求实数的取值范围. 解：（1），.当时，则在上恒成立，所以在上单调递增；当时，由，得，由，得，所以在上单调递减，在上单调递增.综上所述，当时，函数在上单调递增；当时，函数在上单调递减，在上单调递增；（2）由题意知在上恒成立，即恒成立，令，其中，则.当时，则；当时，则.所以在上单调递减，在上单调递增，则.所以实数的取值范围为.