2021玉溪高二上学期教学质量检测数学（理）试题含答案

这是一份2021玉溪高二上学期教学质量检测数学（理）试题含答案

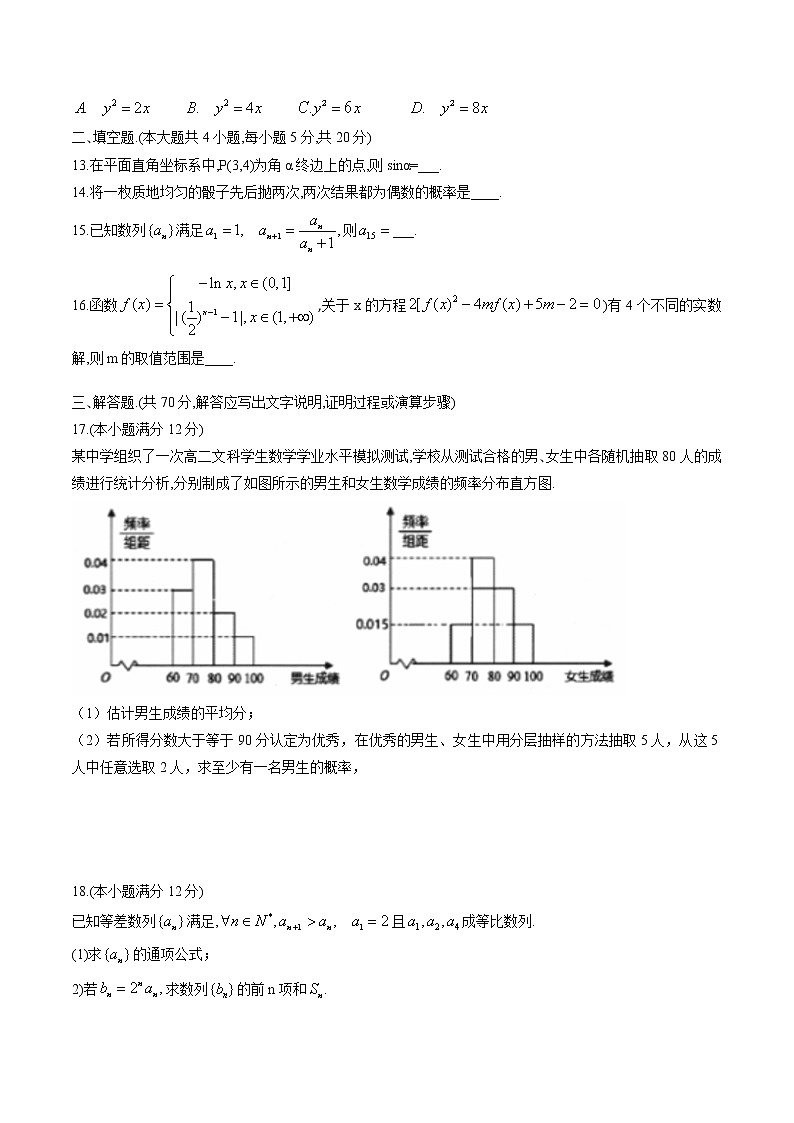
玉溪市2020一2021学年上学期高二年级期末教学质量检测理科数学试卷一､选择题.(本大题共12小题,每小题5分,共60分)1.已知,则()A.{x|x>0} B.{x|x<1} 2.设已知则a,b,c的大小关系为()A.a>b>c B.b>c>a C.c>b>a D.a>c>b3.在△ABC中,点D是线段BC上靠近B的三等分点,下列等式成立的是( ) 4.已知a b∈R且a>b,下列不等式正确的是() C.a-b>0 D.a+b>05.在如图所示的程序框图中,如果输入的n=5,那么输出的i等于()A.3 B.4 C.5 D.66.若x,y满足约束条件,z=2x-3y的最大值为()A.9 B.6 C.3 D.17.已知直线l:x+2y-3=0与圆交于A､B两点,求线段AB的中垂线方程()A.2x-y-2=0 B.2x-y-4=0 8.把5名同学分配到图书馆、食堂、学生活动中心做志愿者，每个地方至少去一个同学，不同的安排方法共有（）种.A.60 B.72 C.96 D.1509.如图是由一个棱长为2的正方体截去一个三棱锥后剩余几何体的三视图,该几何体的体积为（）A. B. C. D.10.已知把f(x)的图象上所有点的横坐标缩短为原来的倍,纵坐标不变,再向右平移个单位,得到g(x)的函数图象,则()A.g(x)图象的对称轴为B.g(x)图象的对称轴为k∈Z且为奇函数C.g(x)图象的对称轴为x=π+2kπ, k∈Z且为奇函数D.g(x)图象的对称轴为11.设是三条不同的直线,α,β, γ是三个不同的平面,则下列命题是真命题的是()A.若则B.若则C.若则D.若则12.已知抛物线C:(的焦点为F,过点F且斜率为2的直线为1,M(-4,0),若抛物线C上存在一点N,使M, N关于直线对称,抛物线C的方程为( ) 二､填空题.(本大题共4小题,每小题5分,共20分)13.在平面直角坐标系中,P(3,4)为角α终边上的点,则sinα=___.14.将一枚质地均匀的骰子先后抛两次,两次结果都为偶数的概率是____.15.已知数列满足则___.16.函数,关于x的方程)有4个不同的实数解,则m的取值范围是____.三､解答题.(共70分,解答应写出文字说明,证明过程或演算步骤)17.(本小题满分12分)某中学组织了一次高二文科学生数学学业水平模拟测试,学校从测试合格的男､女生中各随机抽取80人的成绩进行统计分析,分别制成了如图所示的男生和女生数学成绩的频率分布直方图.（1）估计男生成绩的平均分；（2）若所得分数大于等于90分认定为优秀，在优秀的男生、女生中用分层抽样的方法抽取5人，从这5人中任意选取2人，求至少有一名男生的概率，18.(本小题满分12分)已知等差数列满足,且成等比数列.(1)求的通项公式；2)若求数列的前n项和19.(本小题满分12分)如图,在平面四边形ABCD中,∠A=45°∠ADC=90°,AB=2 BD=5.(1)求sin∠ADB;(2)若求BC.20.(本小题满分12分)如图,在四棱锥P-ABCD中,底面ABCD是边长为2的正方形,∠ADP=90°,PD=AD,∠PDC=60°,E为PD中点.(1)求证:PB//平面ACE:（2）求二面角P-BC-D的余弦值.21.(本小题满分12分)已知椭圆的离心率为右焦点到左顶点的距离是(1)求椭圆C的方程;(2)设点M为椭圆上位于第一象限内一动点,A,B分别为椭圆的左顶点和下顶点,直线MB与x轴交于点C,直线MA与y轴交于点D,求证:四边形ABCD的面积为定值.22.(本小题满分12分)已知(1)判断函数f(x)在[0,+∞)的单调性,并证明.(2)对于任意存在使得成立,求a的取值范围.