

2021西宁海湖中学高二上学期第一阶段测试数学试题含答案
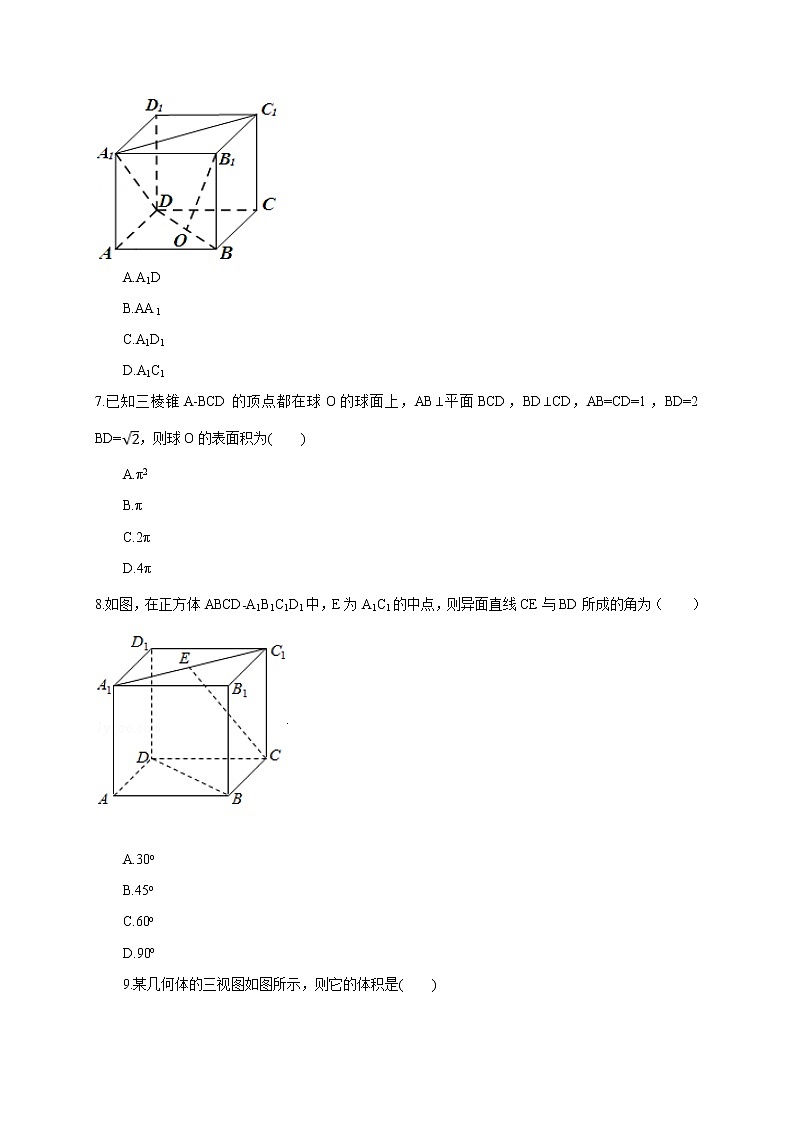
展开绝密★启用前西宁市海湖中学2020—2021学年度第一学期高二数学第一阶段测试题时间:120分钟 满分:100分单选题1.某人用如图所示的纸片沿折痕折后粘成一个四棱锥形的“走马灯“,正方形做灯底,且有一个三角形面上写上了“年”字,当灯旋转时,正好看到“新年快乐”的字样,则在①、②、③处可依次写上( ) A.乐、新、快B.快、新、乐C.新、乐、快D.乐、快、新2.如图,在正方体ABCD-A1B1C1D1中,E、F分别为BC、BB1的中点,则下列直线中与直线EF相交的是( ) A.直线AA1B.直线A1B1C.直线A1D1D.直线B1C13.已知圆柱的上、下底面的中心分别为O1,O2,过直线O1O2的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为( ) A.122πB.12πC.82πD.10π4.等边三角形的边长为a,它绕其一边所在的直线旋转一周,则所得旋转体的体积为( ) A.a3B.a3C.a3D.a35.如图,正方体ABCD﹣A1B1C1D1的棱长为1,动点E在线段A1C1上,F,M分别是AD,CD的中点,则下列结论中错误的是( ) A.FM∥A1C1B.BM⊥平面CC1FC.三棱锥B﹣CEF的体积为定值D.存在点E,使得平面BEF∥平面CC1D1D6.如图,O为正方体ABCD-A1B1C1D1的底面ABCD的中心,则下列直线中与B1O垂直的是( ) A.A1DB.AA1C.A1D1D.A1C17.已知三棱锥A-BCD的顶点都在球O的球面上,AB⊥平面BCD,BD⊥CD,AB=CD=1,BD=2 BD=,则球O的表面积为( ) A.π2B.πC.2πD.4π8.如图,在正方体ABCD﹣A1B1C1D1中,E为A1C1的中点,则异面直线CE与BD所成的角为( ).A.30oB.45oC.60oD.90o9.某几何体的三视图如图所示,则它的体积是( )A.B.C.D. 10.设α为平面,a、b为两条不同的直线,则下列叙述正确的是( ) A.若a∥α,b∥α,则a∥bB.若a⊥α,a∥b,则b⊥αC.若a⊥α,a⊥b,则b∥αD.若a∥α,a⊥b,则b⊥α11.已知m、n是两条不同直线,α、β、γ是三个不同平面,以下有三种说法: ①若α∥β,β∥γ,则γ∥α; ②若α⊥γ,β∥γ,则α⊥β; ③若m⊥β,m⊥n, n⊊,,则n∥β. 其中正确命题的个数是( ) A.3个B.2个C.1个D.0个12.水平放置的△ABC,用斜二测画法作出的直观图是如图所示的△A'B'C',其中O'A'=O'B'=1,,则△ABC绕AB所在直线旋转一周后形成的几何体的表面积为( ) A.B.C.D.填空题13.在三棱锥B﹣ACD中,BA,BC,BD两两垂直,BC=2,BD=4,三棱锥B﹣ACD的侧面积为13,则该三棱锥外接球的表面积为_______. 14.已知圆锥的侧面积(单位:cm2)为,且它的侧面展开图是一个半圆,则这个圆锥的底面半径(单位:cm)是_______. 15.在正方体ABCD-A1B1C1D1中,六个面内与BD成60o角的对角线共有_______条. 16.中国有悠久的金石文化,印信是金石文化的代表之一.印信的形状多为长方体、正方体或圆柱体,但南北朝时期的官员独孤信的印信形状是“半正多面体”(图1).半正多面体是由两种或两种以上的正多边形围成的多面体.半正多面体体现了数学的对称美.图2是一个棱数为48的半正多面体,它的所有顶点都在同一个正方体的表面上,且此正方体的棱长为1.则该半正多面体共有______个面,其棱长为_______. 三、解答题17.如图(1),在四棱锥P-ABCD中,底面为正方形,PC与底面ABCD垂直,图(2)为该四棱锥的正视图和侧视图,它们是腰长为6cm的全等的等腰直角三角形. (10分)(1) 根据图所给的正视图、侧视图,画出相应的俯视图,并求出该俯视图的面积;(5分)(2)在四棱锥P-ABCD中,求PA的长(5分)18.如图,在正方体ABCD﹣A1B1C1D1中,AB=1. (12分)(1) 求异面直线A1B与B1C所成的角;(6分) (2) 求证:平面A1BD∥平面B1CD1.(6分)19.如图,AB是圆O的直径,点C是圆O上的动点,过动点C的直线SC垂直于圆O所在的平面,D,E分别是SA,SC的中点. (12分)(1) 证明:DE∥平面ABC;(6分) (2) 平面SAC平面SBC.(6分)20.如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点。 (Ⅰ)证明:BC1∥平面A1CD; (Ⅱ)设AA1=AC=CB=2,AB=,求三棱锥C-A1DE的体积。 (12分)21.如图,在四棱锥P﹣ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC=1,点E是PC的中点,作EFPB交PB于点F. (12分)(1) 求证:PA∥平面EDB;(6分)(2) 求证:PB平面EFD.(6分)22.如图,已知四棱锥P﹣ABCD,底面ABCD是等腰梯形,且AB∥CD,O是AB中点,PO平面ABCD,PO=CD=DA=AB=4,M是PA中点. (12分)(1) 证明:平面PBC∥平面ODM(6分); (2) 求点A到平面PCD的距离(6分). B D B A D D D D A B A B13. 29π14. 115. 816. 26 -117.如图(1),在四棱锥P-ABCD中,底面为正方形,PC与底面ABCD垂直,图(2)为该四棱锥的正视图和侧视图,它们是腰长为6cm的全等的等腰直角三角形. (12分)(1) 根据图所给的正视图、侧视图,画出相应的俯视图,并求出该俯视图的面积;(5分)【正确答案】解:该四棱锥的俯视图为边长为6cm的正方形(内含对角线),如图,其面积为36cm2. 解:该四棱锥的俯视图为边长为6cm的正方形(内含对角线),如图,其面积为36cm2.【答案解析】该四棱锥的俯视图为边长为6cm的正方形(内含对角线),如图,即可得出面积.(2)在四棱锥P-ABCD中,求PA的长(7分)【正确答案】 解:由侧视图可求得 . 由正视图可知AD=6且AD⊥PD, 所以在Rt△APD中, . 解:由侧视图可求得 . 由正视图可知AD=6且AD⊥PD, 所以在Rt△APD中, . 【答案解析】 利用勾股定理即可得出. 21. 如图,在四棱锥P﹣ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC=1,点E是PC的中点,作EFPB交PB于点F. (10分)(1) 求证:PA∥平面EDB;(4分)【正确答案】 证明: 连结AC、BD,交于点O,连结OE, ∵底面ABCD是正方形,∴O是AC中点, ∵点E是PC的中点,∴OE∥PA, ∵OE⊂平面EDB,PA⊄平面EDB, ∴PA∥平面EDB. 证明: 连结AC、BD,交于点O,连结OE, ∵底面ABCD是正方形,∴O是AC中点, ∵点E是PC的中点,∴OE∥PA, ∵OE⊂平面EDB,PA⊄平面EDB, ∴PA∥平面EDB.【答案解析】连结AC、BD,交于点O,连结OE,推导出OE∥PA,由此能证明PA∥平面EDB.(2) 求证:PB平面EFD.(6分)【正确答案】 解:∵PD=DC=1,点E是PC的中点,∴DE⊥PC, ∵底面ABCD是正方形,侧棱PD⊥底面ABCD, ∴PD⊥BC,CD⊥BC,又PD∩DC=D, ∴BC⊥平面PDC,∴DE⊥BC, ∵PC∩BC=C,∴DE⊥平面PBC,∴DE⊥PB, ∵EF⊥PB,EF∩DE=E, ∴PB⊥平面EFD. 解:∵PD=DC=1,点E是PC的中点,∴DE⊥PC, ∵底面ABCD是正方形,侧棱PD⊥底面ABCD, ∴PD⊥BC,CD⊥BC,又PD∩DC=D, ∴BC⊥平面PDC,∴DE⊥BC, ∵PC∩BC=C,∴DE⊥平面PBC,∴DE⊥PB, ∵EF⊥PB,EF∩DE=E, ∴PB⊥平面EFD.【答案解析】推导出DE⊥PC,PD⊥BC,CD⊥BC,从而DE⊥BC,进而DE⊥平面PBC,DE⊥PB,再由EF⊥PB,能证明PB⊥平面EFD. 18.如图,在正方体ABCD﹣A1B1C1D1中,AB=1. (12分)(1) 求异面直线A1B与B1C所成的角;(6分)【正确答案】 解:连接A1D、DB.由正方体可得A1B1∥DC,A1B1=DC, ∴对角面A1B1CD是一个平行四边形,∴B1C∥A1D. ∴∠BA1D或其补角即为异面直线A1B与 B1C所成的角, ∵△A1BD是一个等边三角形, ∴∠BA1D=60°即为异面直线A1B与 B1C所成的角; 解:连接A1D、DB.由正方体可得A1B1∥DC,A1B1=DC, ∴对角面A1B1CD是一个平行四边形,∴B1C∥A1D. ∴∠BA1D或其补角即为异面直线A1B与 B1C所成的角, ∵△A1BD是一个等边三角形, ∴∠BA1D=60°即为异面直线A1B与 B1C所成的角;【答案解析】通过平移先作出异面直线所成的角,进而求出即可;(2) 求证:平面A1BD∥平面B1CD1.(6分)【正确答案】 证明:由(1)可知:A1D∥B1C,而A1D⊄平面B1CD1,B1C⊂平面B1CD1, ∴A1D∥平面B1CD1, 同理可得A1B∥平面B1CD1, 又∵A1D∩A1B=A1,∴平面A1BD∥平面B1CD1.证明:由(1)可知:A1D∥B1C,而A1D⊄平面B1CD1,B1C⊂平面B1CD1, ∴A1D∥平面B1CD1, 同理可得A1B∥平面B1CD1, 又∵A1D∩A1B=A1,∴平面A1BD∥平面B1CD1. 【答案解析】利用线面、面面平行的判定定理即可证明. 19.如图,AB是圆O的直径,点C是圆O上的动点,过动点C的直线SC垂直于圆O所在的平面,D,E分别是SA,SC的中点. (12分)(1) 证明:DE∥平面ABC;(4分)【正确答案】 证明:∵D,E分别是SA,SC的中点,∴DE∥AC, 又∵DE⊄平面ABC,AC⊂平面ABC,∴DE∥平面ABC; 证明:∵D,E分别是SA,SC的中点,∴DE∥AC, 又∵DE⊄平面ABC,AC⊂平面ABC,∴DE∥平面ABC;【答案解析】由D,E分别是SA,SC的中点,可得DE∥AC,从而得到DE∥平面ABC.(2) 平面SAC平面SBC.(8分)【正确答案】 解:∵AB为圆O的直径,∴AC⊥BC, ∵SC垂直于圆O所在的平面,∴SC⊥AC, 而BC∩SC=C,∴AC⊥平面SBC, ∵DE∥AC,∴DE⊥平面SBC, 又DE⊂平面SAC,∴平面SAC⊥平面SBC.解:∵AB为圆O的直径,∴AC⊥BC, ∵SC垂直于圆O所在的平面,∴SC⊥AC, 而BC∩SC=C,∴AC⊥平面SBC, ∵DE∥AC,∴DE⊥平面SBC, 又DE⊂平面SAC,∴平面SAC⊥平面SBC.【答案解析】由AB为圆O的直径,得AC⊥BC,再由SC垂直于圆O所在的平面,得SC⊥AC,可得AC⊥平面SBC,结合DE∥AC,得DE⊥平面SBC,从而得到平面SAC⊥平面SBC.20.如图,直三棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点。 (Ⅰ)证明:BC1∥平面A1CD; (Ⅱ)设AA1=AC=CB=2,AB=,求三棱锥C-A1DE的体积。 (12分)【正确答案】 (Ⅰ) 见解析,(Ⅱ)1【答案解析】解:(Ⅰ)连接AC1 交A1C于点F,则F为AC1的中点. 又D是AB的中点,连结DF,则BC1∥DF。 因为DF平面A1CD,BC1平面A1CD, 所以BC1∥平面A1CD。 (Ⅱ)因为ABC-A1B1C1是直三棱柱,所以AA1⊥CD,由已知AC=CB,D为AB的中点,的以CD⊥AB。又AA1∩AB=A,于是CD⊥平面ABB1A。 由AA1=AC=CB=2,AB=得 故A1D2+DE2=A1E2,即DE⊥A1D. 22.如图,已知四棱锥P﹣ABCD,底面ABCD是等腰梯形,且AB∥CD,O是AB中点,PO平面ABCD,PO=CD=DA=AB=4,M是PA中点. (12分)(1) 证明:平面PBC∥平面ODM;(6分)【正确答案】 证明:由题意,CD∥BO,CD=BO, ∴四边形OBCD为平行四边形,∴BC∥OD. 又∵AO=OB,AM=MP,∴OM∥PB 又OM⊄平面PBC,PB⊂平面PBC, ∴OM∥平面PBC 同理,OD∥平面PBC, 又OM∩OD=O, ∴平面PBC∥平面ODM. 证明:由题意,CD∥BO,CD=BO, ∴四边形OBCD为平行四边形,∴BC∥OD. 又∵AO=OB,AM=MP,∴OM∥PB 又OM⊄平面PBC,PB⊂平面PBC, ∴OM∥平面PBC 同理,OD∥平面PBC, 又OM∩OD=O, ∴平面PBC∥平面ODM.【答案解析】证明平面PBC∥平面ODM,只需证明OM∥平面PBC,OD∥平面PBC,利用线面平行的判定定理可证;(2) 求点A到平面PCD的距离. (6分)【正确答案】 解:设求点A到平面PCD的距离为d. ∵PO⊥平面ABCD,PO=CD=DA=AB=4,M是PA中点,V三棱锥A﹣PCD=V三棱锥P﹣ACD ∴ ∴. 解:设求点A到平面PCD的距离为d. ∵PO⊥平面ABCD,PO=CD=DA=AB=4,M是PA中点,V三棱锥A﹣PCD=V三棱锥P﹣ACD ∴ ∴.【答案解析】利用V三棱锥A﹣PCD=V三棱锥P﹣ACD,可求点A到平面PCD的距离.
2020西宁海湖中学高二下学期第一阶段考试数学(理)试题含答案: 这是一份2020西宁海湖中学高二下学期第一阶段考试数学(理)试题含答案,共18页。
2020西宁海湖中学高二下学期第一阶段考试数学(文)试题含答案: 这是一份2020西宁海湖中学高二下学期第一阶段考试数学(文)试题含答案
2021西宁海湖中学高二上学期第二次阶段测试数学试题含答案: 这是一份2021西宁海湖中学高二上学期第二次阶段测试数学试题含答案









