2021兰州第二十七中学高一期末考试数学试卷含答案

www.ks5u.com兰州二十七中2020—2021学年度第一学期期末试卷

高一数学

本试卷分第I卷(选择题)和第II卷(非选择题)两部分. 满分150分, 考试时间为120分钟.

第Ⅰ卷(选择题  共60分)

一、选择题(下列各题只有一个选项符合要求，请将正确选项的代码填入答题卡中，每小题5分，共60分)

1、下列命题为真命题的是（    ）

1. 平行于同一平面的两条直线平行；  B.与某一平面成等角的两条直线平行；

3. 垂直于同一直线的两条直线平行；  D. 垂直于同一平面的两条直线平行。

2、下列命题中错误的是（    ）

1. 如果α⊥β，那么α内一定存在直线平行于平面β；
2. 如果α⊥β，那么α内所有直线都垂直于平面β；
3. 如果平面α不垂直平面β，那么α内一定不存在直线垂直于平面β；
4. 如果α⊥γ，β⊥γ，α∩β＝l,那么l⊥γ.

3、右图的正方体ABCD-A’B’C’D’中,异面直线AA’与BC所成的角是（    ）

A.  300       B.450      C.  600      D. 900

4、右图的正方体ABCD- A’B’C’D’中，二面角D’-AB-D的大小是（    ）

A.  300       B.450      C.  600      D. 900

5、直线5x-2y-10=0在x轴上的截距为a,在y轴上的截距为b,则（    ）

A.a=2,b=5     B.a=2,b=     C.a=,b=5    D.a=,b=

6、直线2x-y=7与直线3x+2y-7=0的交点是（    ）

A  (3,-1)  B  (-1,3)  C  (-3,-1)  D  (3,1)

7、过点P(4,-1)且与直线3x-4y+6=0垂直的直线方程是（    ）

A  4x-3y-19=0      B  4x+3y-13=0 

C  3x-4y-16=0      D   3x+4y-8=0

8、点的内部，则的取值范围是（   ）

(A)     (B)     (C)   (D)

9、已知一个铜质的五棱柱的底面积为16cm2,高为4cm，现将它熔化后铸成一个正方体的铜块（不计损耗），那么铸成的铜块的棱长是（   ）

A. 2cm      B.     C.4cm      D.8cm

10、圆C1: 与圆C2:的位置关系是（    ）

A、外离     B  相交     C  内切     D  外切

11、已知A(x,5－x,2x－1)，B(1，x＋2,2－x)，当|AB|取最小值时，x的值为(　　)

A．19      B．－           C.      D.

12、的最小值为（     ）

A. 2        B. 3          C. 4         D. 5

第Ⅱ卷(非选择题  共90分)

二、填空题 (本大题共4小题，每小题5分，共20分。请把正确答案填在答题卡的横线上)

13、底面直径和高都是4cm的圆锥的侧面积为                 cm2.

14、若直线平行，则              .

15、半径为 a 的球放在墙角，同时与两墙面和地面相切，那么球心到墙角顶点的距离为________________.

16、若函数f(x)＝|x2－2x|－a有两个零点， 则a的取值范围是_______________.

三、解答题 (本大题6小题，共70分.解答时应写出必要的文字说明、证明过程或演算步骤,请将解题过程填写在答题框中,否则不计分).

17、（10分）已知三角形ABC的顶点坐标为A（-1，5）、B（-2，-1）、C（4，3），M是BC边上的中点。

（1）求AB边所在直线的方程；

（2）求中线AM的长。

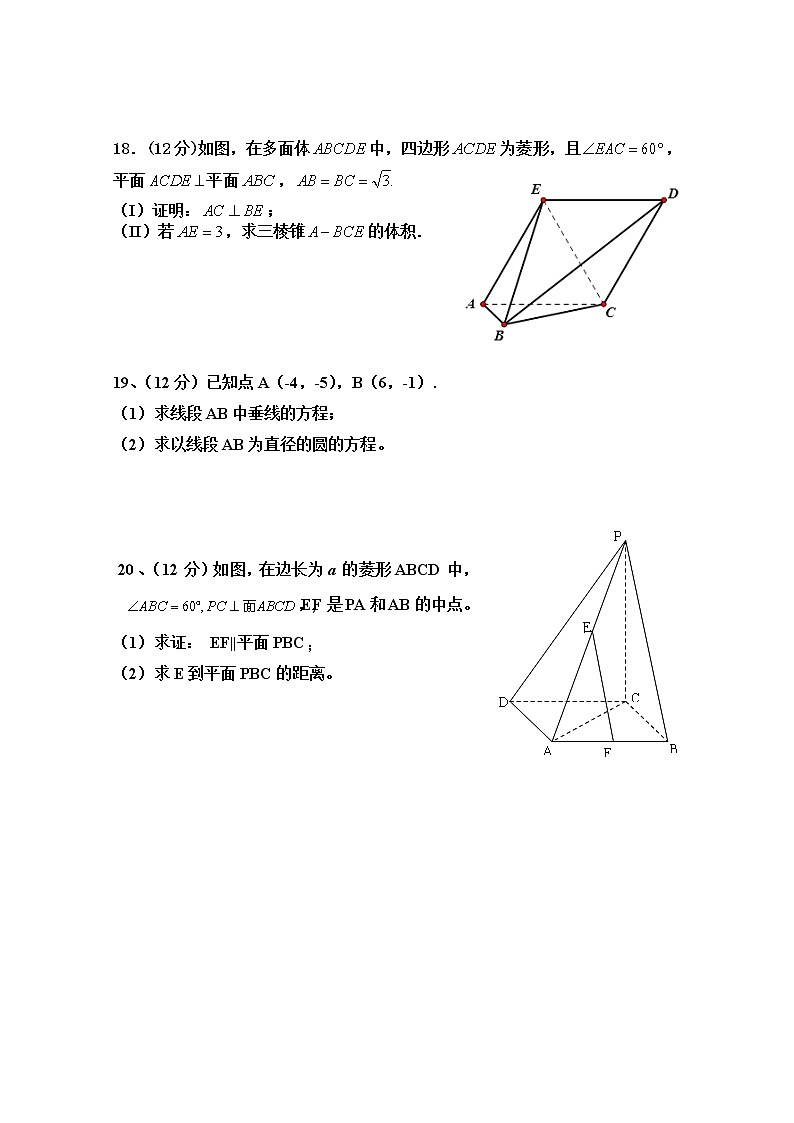
18．(12分)如图，在多面体中，四边形为菱形，且，平面平面，

（I）证明：；

（II）若，求三棱锥的体积．

19、（12分）已知点A（-4，-5），B（6，-1）.

（1）求线段AB中垂线的方程；

（2）求以线段AB为直径的圆的方程。

20、（12分）如图，在边长为a的菱形ABCD中，，E,F是PA和AB的中点。

（1）求证： EF||平面PBC ;

（2）求E到平面PBC的距离。

21、（12分）已知关于x,y的方程C:.

（1）当m为何值时，方程C表示圆。

（2）若圆C与直线l:x+2y-4=0相交于M,N两点，且MN=,求m的值。

22、（12分）如图，在底面是直角梯形的四棱锥S-ABCD中，

(1)求证：

(3)求SC与底面ABCD所成角的正切值.

数学答案

一、选择题（12×5分=60分）

二、填空题（4×5分=20分）

13、     14、    15、   16、

三、解答题

17、解：（1）方法一：由两点式写方程得 ，

即  6x-y+11=0

方法二：直线AB的斜率为 

     直线AB的方程为 

     即  6x-y+11=0

（2）设M的坐标为（），则由中点坐标公式得

   故M（1，1）

.

18、解: （I）如图2，取的中点为，连接，．

因为，所以．

因为四边形为菱形，所以，

因为，所以为等边三角形，

所以，所以．

又

所以平面．

又因为平面，所以．   ··············6分

（II）    ··········9分

在等边三角形中，

在中, 即

所以   ·········12分

19、解：(1) 由中点坐标公式得线段AB的中点坐标为C（1，-3）,

可得线段AB中垂线的斜率为 所以线段AB中垂线方程为 即

(2)设所求圆的方程为：, 则

    由中点坐标公式得线段AB的中点坐标为C（1，-3）

    故所求圆的方程为：.

20、（1）证明：

          又

          故

（2）解：在面ABCD内作过F作

        又 ，，

又，故点E到平面PBC的距离等于点F到平面PBC的距离FH。

      在直角三角形FBH中，，

故点E到平面PBC的距离等于点F到平面PBC的距离等于。

21、解：（1）方程C可化为 

        显然  时方程C表示圆。

（2）圆的方程化为 

     圆心 C（1，2），半径 

     则圆心C（1，2）到直线l:x+2y-4=0的距离为

，有

得 

22、（1）证明：

又

（2）解：连结AC,则就是SC与底面ABCD所成的角。

在三角形SCA中，SA=1,AC=,