2021天津市六校高一上学期期末联考数学试题含答案

这是一份2021天津市六校高一上学期期末联考数学试题含答案试卷主要包含了 设集合，，则， 已知命题， 设，则“，”是“”的， 函数， 设，，，则、、的大小关系为， 若，，，，则等内容，欢迎下载使用。

一､选择题(本题共9小题，每题4分，共36分)
1. 设集合，，则（ ）
A. B. C. D.
2. 已知命题：，总有，则为（ ）
A. ，使得B. ，使得
C. ，总有D. ，使得
3. 设，则“，”是“”的（ ）
A. 充分不必要条件B. 必要不充分条件
C. 充要条件D. 既不充分也不必要条件
4. 函数（且）的图象可能为（ ）
A. B. C. D.
5. 设，，，则、、的大小关系为（ ）
A. B. C. D.
6. 已知在区间上为减函数，则实数的取值范围是（ ）
A. B. C. D.
7. 若，，，，则（ ）
A. B. C. D.
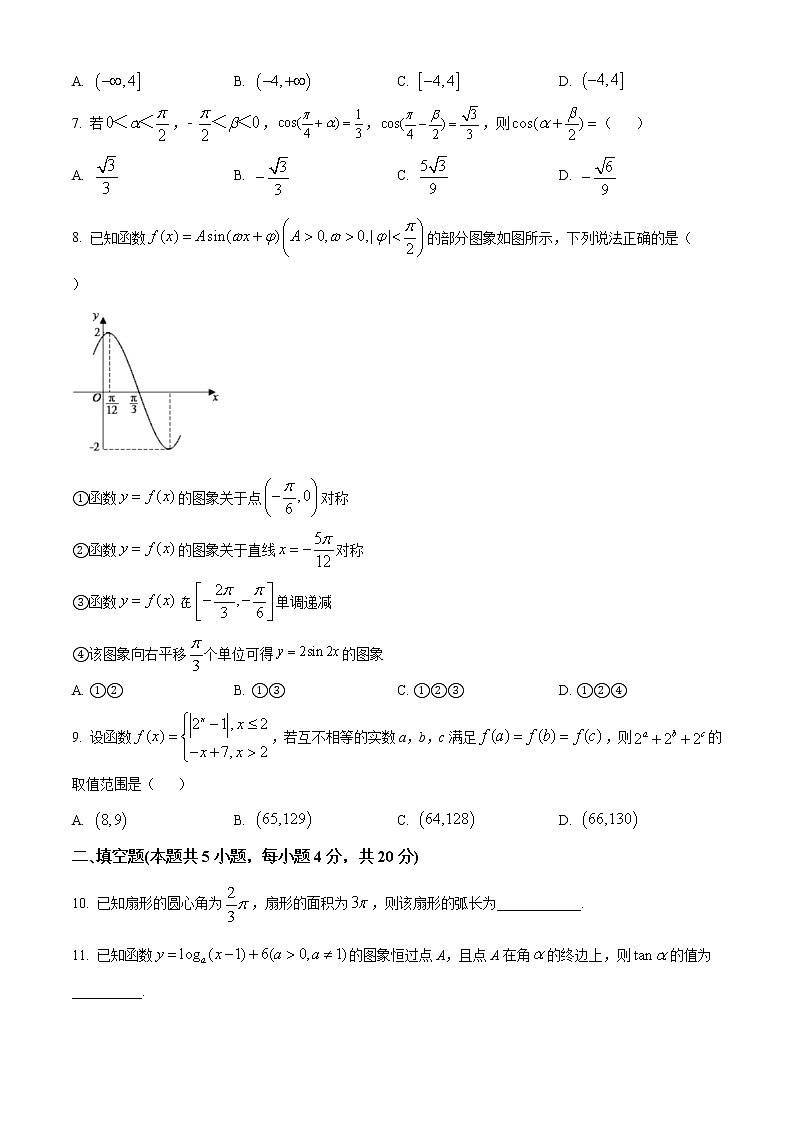
8. 已知函数的部分图象如图所示，下列说法正确的是（ ）
①函数的图象关于点对称
②函数的图象关于直线对称
③函数单调递减
④该图象向右平移个单位可得的图象
A. ①②B. ①③C. ①②③D. ①②④
9. 设函数，若互不相等的实数a，b，c满足，则的取值范围是（ ）
A. B. C. D.
二､填空题(本题共5小题，每小题4分，共20分)
10. 已知扇形的圆心角为，扇形的面积为，则该扇形的弧长为____________.
11. 已知函数的图象恒过点A，且点A在角的终边上，则的值为__________.
12. 设函数，若，，则函数的零点的个数是__________.
13. 对任意的，不等式恒成立，则实数的取值范围是__________．
14. 已知函数，，若对任意，总存在，使得成立，则实数a的取值范围为__________.
三､解答题(本大题共5小题，共64分)
15. 设函数定义域为A，集合.
（1）求集合A，B，并求；
（2）若集合，且，求实数a的取值范围.
16. 已知
（1）化简，并求；
（2）若，求的值；
（3）求函数的值域.
17. 某工厂准备引进一种新型仪器的生产流水线，已知投资该生产流水线需要固定成本1000万元，每生产x百台这种仪器，需另投入成本f(x)万元，假设生产的仪器能全部销售完，且售价为每台3万元.
（1）求利润g(x)（万元）关于产量x（百台）的函数关系式；
（2）当产量为多少时，该工厂所获利润最大？并求出最大利润.
18. 已知函数周期是.
（1）求的解析式，并求的单调递增区间；
（2）将图像上所有点的横坐标扩大到原来的2倍，再向左平移个单位，最后将整个函数图像向上平移个单位后得到函数的图像，若时，恒成立，求m得取值范围.
19. 已知函数的图象过点，.
（1）求函数的解析式；
（2）若函数在区间上有零点，求整数k的值；
（3）设，若对于任意，都有，求m的取值范围.
2020~2021学年度第一学期期末六校联考
高一数学（答案）
一､选择题(本题共9小题，每题4分，共36分)
1. 设集合，，则（ ）
A. B. C. D.
【答案】B
2. 已知命题：，总有，则为（ ）
A. ，使得B. ，使得
C. ，总有D. ，使得
【答案】B
3. 设，则“，”是“”的（ ）
A. 充分不必要条件B. 必要不充分条件
C. 充要条件D. 既不充分也不必要条件
【答案】A
4. 函数（且）的图象可能为（ ）
A. B. C. D.
【答案】D
5. 设，，，则、、的大小关系为（ ）
A. B. C. D.
【答案】B
6. 已知在区间上为减函数，则实数的取值范围是（ ）
A. B. C. D.
【答案】C
7. 若，，，，则（ ）
A. B. C. D.
【答案】C
8. 已知函数的部分图象如图所示，下列说法正确的是（ ）
①函数的图象关于点对称
②函数的图象关于直线对称
③函数单调递减
④该图象向右平移个单位可得的图象
A. ①②B. ①③C. ①②③D. ①②④
【答案】A
9. 设函数，若互不相等的实数a，b，c满足，则的取值范围是（ ）
A. B. C. D.
【答案】D
二､填空题(本题共5小题，每小题4分，共20分)
10. 已知扇形的圆心角为，扇形的面积为，则该扇形的弧长为____________.
【答案】
11. 已知函数的图象恒过点A，且点A在角的终边上，则的值为__________.
【答案】3
12. 设函数，若，，则函数的零点的个数是__________.
【答案】2
13. 对任意的，不等式恒成立，则实数的取值范围是__________．
【答案】
14. 已知函数，，若对任意，总存在，使得成立，则实数a的取值范围为__________.
【答案】
三､解答题(本大题共5小题，共64分)
15. 设函数定义域为A，集合.
（1）求集合A，B，并求；
（2）若集合，且，求实数a的取值范围.
【答案】（1），，；（2）.
16. 已知
（1）化简，并求；
（2）若，求的值；
（3）求函数的值域.
【答案】（1），；（2）；（3）
17. 某工厂准备引进一种新型仪器的生产流水线，已知投资该生产流水线需要固定成本1000万元，每生产x百台这种仪器，需另投入成本f(x)万元，假设生产的仪器能全部销售完，且售价为每台3万元.
（1）求利润g(x)（万元）关于产量x（百台）的函数关系式；
（2）当产量为多少时，该工厂所获利润最大？并求出最大利润.
【答案】（1）；（2）产量为5000台时，该工厂获得利润最大，且最大利润为1900万元.
18. 已知函数周期是.
（1）求的解析式，并求的单调递增区间；
（2）将图像上所有点的横坐标扩大到原来的2倍，再向左平移个单位，最后将整个函数图像向上平移个单位后得到函数的图像，若时，恒成立，求m得取值范围.
【答案】（1），单调递增区间为，；（2）.
19. 已知函数的图象过点，.
（1）求函数的解析式；
（2）若函数在区间上有零点，求整数k的值；
（3）设，若对于任意，都有，求m的取值范围.
【答案】（1）；（2）的取值为2或3；（3）.