

2020海南省海南枫叶国际学校高一下学期期末考试数学试题含答案
展开海南枫叶国际学校2019-2020学年度第二学期
高一年级数学学科期末考试试卷
(范围:必修二第六,七,八,九章 )
一、单项选择题(本题共8小题,每小题5分,共40.0分,在每小题给出的四个选项中,只有一项是符合题目要求的.)
- 某幼儿园为了了解全园310名小班学生的身高情况,从中抽取31名学生进行身高测量.下列说法正确的是
A. 总体是310 B. 310名学生中的每一名学生都是个体
C. 样本是31名小班学生 D. 样本容量是31
- 设,则
A. 2 B. C. D. 1
- 已知向量,,则
A. B. C. 2 D.
- 已知中,角A,B,C所对的边分别为a,b,c,若,,,
则
A. 2 B. 1 C. D.
- 已知单位向量,的夹角为,则在下列向量中,与垂直的是
A. B. C. D.
- 已知,,,则
A. B. C. D. 3
- 若棱长为的正方体的顶点都在同一球面上,则该球的表面积为
A. B. C. D.
- 在中,,,,则
A. B. C. D.
二、多项选择题(本题共4小题,每小题5分,共20.0分,在每小题给出的四个选项中,有多项符合题目要求,全部选对的得5分,部分选对的得3分,有选错的得0分)
9.下列说法正确的是
A. 若一个平面经过另一个平面的垂线,则这两个平面相互垂直
B. 若一个平面内的两条直线与另一个平面都平行,则这两个平面相互平行
C. 垂直于同一直线的两条直线相互平行
D. 若两个平面垂直,那么一个平面内与它们的交线垂直的直线与另一个平面也垂直
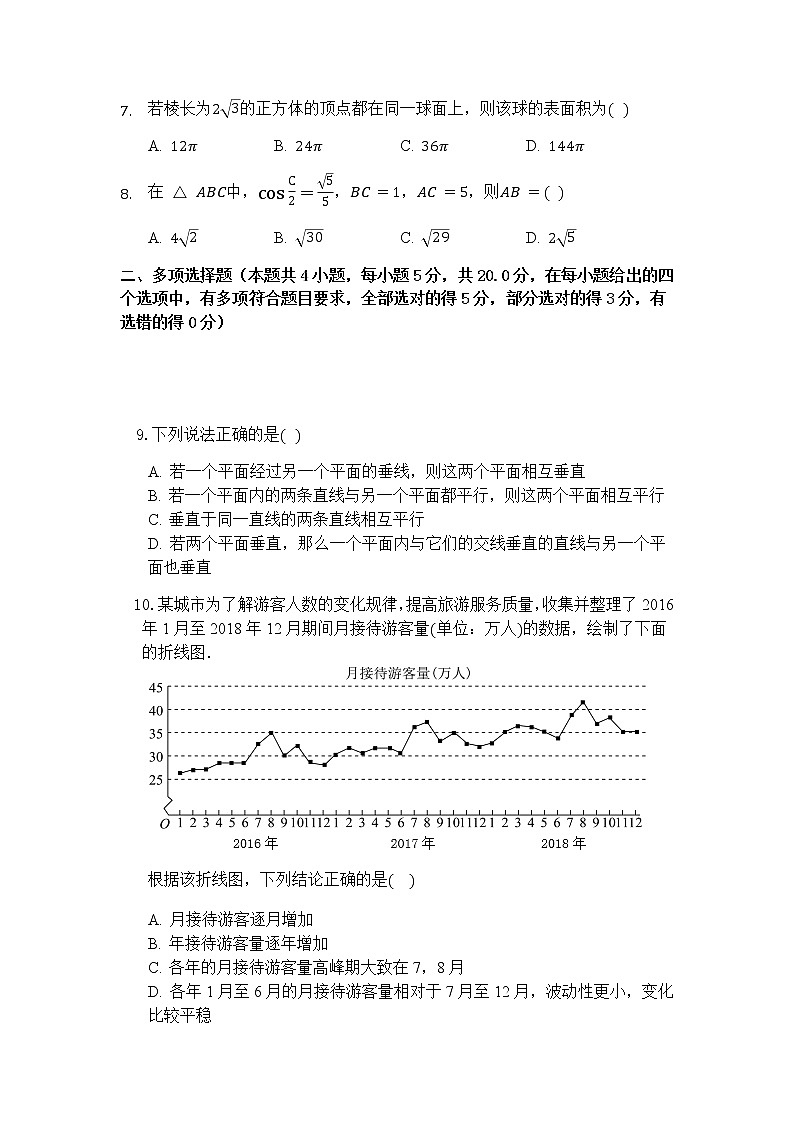
10.某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2016年1月至2018年12月期间月接待游客量单位:万人的数据,绘制了下面的折线图.
根据该折线图,下列结论正确的是
A. 月接待游客逐月增加
B. 年接待游客量逐年增加
C. 各年的月接待游客量高峰期大致在7,8月
D. 各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳
11.在发生公共卫生事件期间,有专业机构认为该事件在一段时间内没有发生大规模群体感染的标志为“连续10天,每天新增疑似病例不超过7人”过去10日,甲、乙、丙、丁四地新增疑似病例数据信息如下:
甲地:中位数为2,极差为5;
乙地:总体平均数为2,众数为2;
丙地:总体平均数为1,总体方差大于0;
丁地:总体平均数为2,总体方差为3.则甲、乙、丙、丁四地中,一定没有发生大规模群体感染的有
A. 甲地 B. 乙地 C. 丙地 D. 丁地
12.将正方形ABCD沿对角线BD折成直二面角,如下四个结论正确是
A. ; B. 是等边三角形;
C. AB与平面BCD所成的角为; D. AB与CD所成的角为.
三、填空题(本大题共4小题,每小题5分,共20.0分)
13.已知复数的实部为0,其中i为虚数单位,则实数a的值是______.
14.在某个容量为100的样本的频率分布直方图中,共有5小长方形,若中间一个小长方形的面积等于其他4个小长方形面积和的,则中间一组的频数为_______.
15.如图所示,正方体的棱长为2,以其所有面的中心为顶点的多面体的体积为______.
|
16.的内角A,B,C的对边分别为a,b,已知,,则的面积为______.
四、解答题(本大题共6小题,17题10分,其余每题12分,共70.0分,解答应写出文字说明,证明过程或演算步骤.)
17.设向量,
若,求的值; 若,求的值.
18.两台机床同时生产直径为10的零件,为了检验产品质量,质量检验员从两台机床生产的产品中各抽出4件进行测量,结果如下:
机床甲 | 10 | 10 | ||
机床乙 | 10 | 10 |
如果你是质量检验员,在收集到上述数据后,请用统计的有关知识判断哪台机床生产的零件质量更符合要求?
19.如图,在直三棱柱中,D,E分别为BC,AC的中点,.
求证: 平面; E.
|
20.统计局就某地居民的月收入情况调查了10000人,并根据所得数据画出了样本频率分布直方图,每个分组包括左端点,不包括右端点,如第一组表示收入在元.
为了分析居民的收入与年龄、职业等方面的关系,必须按月收入再从这10000人中用分层抽样方法抽出100人作进一步分析,则月收入在元的应抽取多少人?
根据频率分布直方图估计样本数据的中位数;
根据频率分布直方图估计样本数据的平均数.
21.已知内角A、B、C的对边分别为a、b、c,
2() = +
1证明:;
2求的最小值.
22.如图,D为圆锥的顶点,O是圆锥底面的圆心,是底面的内接正三角形,P为DO上一点,.
证明:平面平面PAC;
设,圆锥的侧面积为,求三棱锥的体积.
高一数学期末考试题参考答案
一、单选题: DCAD DBCA
二、多选题:(9)AD (10)BCD (11)AD (12ABD
三.填空题
(13)2 (14) 20 ( 15 ) (16).
三、解答题(本大题共6小题,共70分,解答应写出文字说明,证明过程或演算步骤.)
17.解:,,且,
,可得.(5分)
,
,化简得.
因此, (10分)
18.解:先计算平均直径:,
,
由于,
因此,平均直径反映不出两台机床生产的零件的质量优劣.(6分)
再计算方差:
,
.
这说明乙机床生产出的零件直径波动小,
因此,从产品质量稳定性的角度考虑,乙机床生产的零件质量更符合要求.(12分)
19.证明:在直三棱柱中,D,E分别为BC,AC的中点,
,,,
平面,平面,
平面.(6分)
解:在直三棱柱中,E是AC的中点,.
,,
又,平面,
平面,E.(12分)
20.解:月收入在的频率为
,
对应的频数为人,
又抽取的样本容量为100.抽取比例为,
月收入在的这段应抽取人;(4分)
从左数第一组的频率为;
第二组的频率为;第三组的频率为;
,,
中位数位于第三组,设中位数为,
则,解得,中位数为元;(8分)
根据频率分布直方图,计算平均数为:
,
所以样本数据的平均数为元.(12分)
21.解:Ⅰ证明:由得:
;
两边同乘以cosAcosB得,;
;
即;
根据正弦定理,;,
代入得:;;(6分)
Ⅱ;;
,且,当且仅当时取等号;
又a,;;由余弦定理,;
的最小值为.(12分)
22.解:连接OA,OB,OC,是底面的内接正三角形,
所以.
O是圆锥底面的圆心,所以:,
所以,
所以≌≌,
由于.
所以
所以,,AP,平面APC,
由于,
所以平面APC,
由于平面PAB,
所以:平面平面PAC.(6分)
设圆锥的底面半径为r,圆锥的母线长为l,
所以.
由于圆锥的侧面积为,
所以,整理得,
解得.
所以.
由于,解得
则:.(12分)
2022-2023学年海南省海南中学白沙学校高一下学期期末考试数学试题(A卷)含答案: 这是一份2022-2023学年海南省海南中学白沙学校高一下学期期末考试数学试题(A卷)含答案,共11页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。
2022-2023学年海南省海南中学白沙学校高一下学期期末考试数学试题含答案: 这是一份2022-2023学年海南省海南中学白沙学校高一下学期期末考试数学试题含答案,共11页。试卷主要包含了单选题,多选题,填空题,解答题等内容,欢迎下载使用。
精品解析:海南省海南枫叶国际学校2019-2020学年高一下学期期末考试数学试题: 这是一份精品解析:海南省海南枫叶国际学校2019-2020学年高一下学期期末考试数学试题,文件包含精品解析海南省海南枫叶国际学校2019-2020学年高一下学期期末考试数学试题解析版doc、精品解析海南省海南枫叶国际学校2019-2020学年高一下学期期末考试数学试题原卷版doc等2份试卷配套教学资源,其中试卷共23页, 欢迎下载使用。












