人教版数学八年级上册期中复习逐点清练习 第十一讲《全等三角形的判定与性质》（含答案）

人教版数学八年级上册期中复习逐点清练习 第十一讲《全等三角形的判定与性质》（含答案）

建议用时：45分钟    总分50分

一 选择题（每小题3分，共18分）

1．如图，已知AE∥DF，BE∥CF，AC＝BD，则下列说法错误的是（　　）

A．△AEB≌△DFC B．△EBD≌△FCA C．ED＝AF D．EA＝EC

2．工人师傅常用角尺平分一个任意角．作法如下：如图所示，∠AOB是一个任意角，在边OA，OB上分别取OM＝ON，移动角尺，使角尺两边相同的刻度分别与M，N重合，过角尺顶点C的射线OC即是∠AOB的平分线．这种作法的道理是（　　）

A．HL B．SSS C．SAS D．ASA

3．如图，已知AE＝AD，AB＝AC，EC＝DB，下列结论：

①∠C＝∠B；②∠D＝∠E；③∠EAD＝∠BAC；④∠B＝∠E．其中错误的是（　　）

A．①② B．②③ C．③④ D．只有④

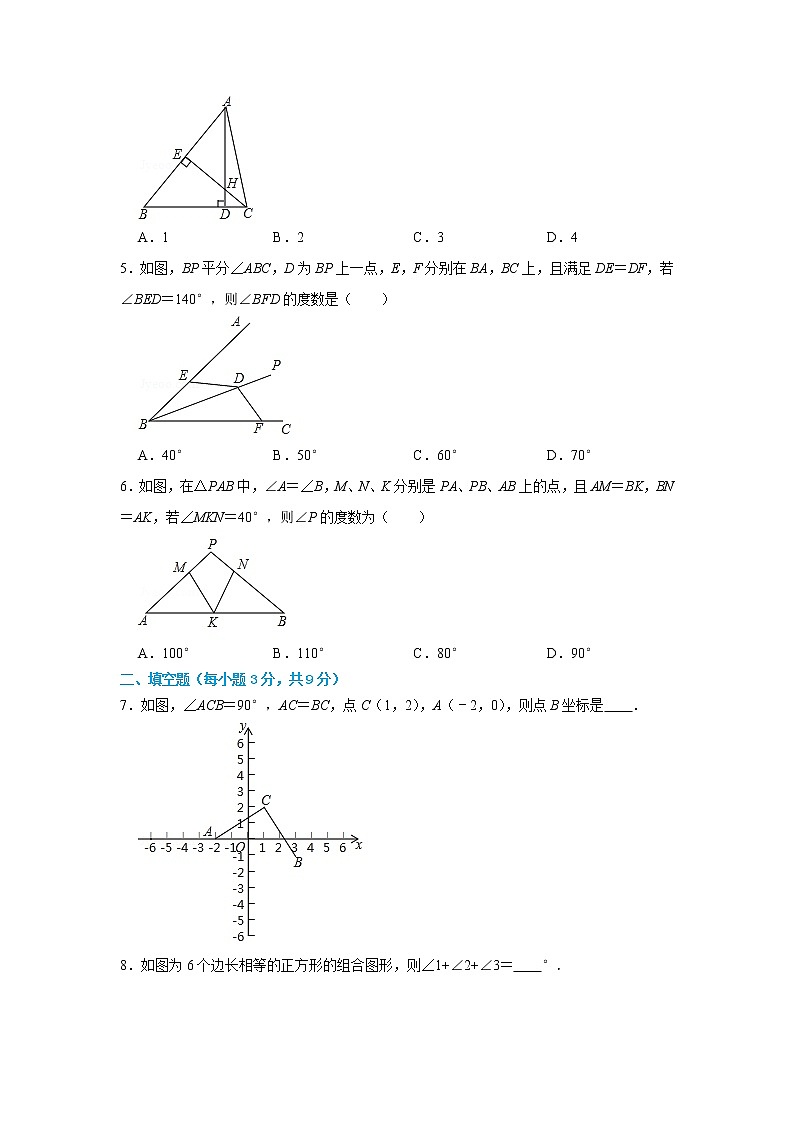
4．如图，在△ABC中，AD⊥BC，CE⊥AB，垂足分别为D、E，AD、CE交于点H，已知EH＝EB＝4，AE＝6，则CH的长为（　　）

A．1 B．2 C．3 D．4

5．如图，BP平分∠ABC，D为BP上一点，E，F分别在BA，BC上，且满足DE＝DF，若∠BED＝140°，则∠BFD的度数是（　　）

A．40° B．50° C．60° D．70°

6．如图，在△PAB中，∠A＝∠B，M、N、K分别是PA、PB、AB上的点，且AM＝BK，BN＝AK，若∠MKN＝40°，则∠P的度数为（　　）

A．100° B．110° C．80° D．90°

二、填空题（每小题3分，共9分）

7．如图，∠ACB＝90°，AC＝BC，点C（1，2），A（﹣2，0），则点B坐标是　　．

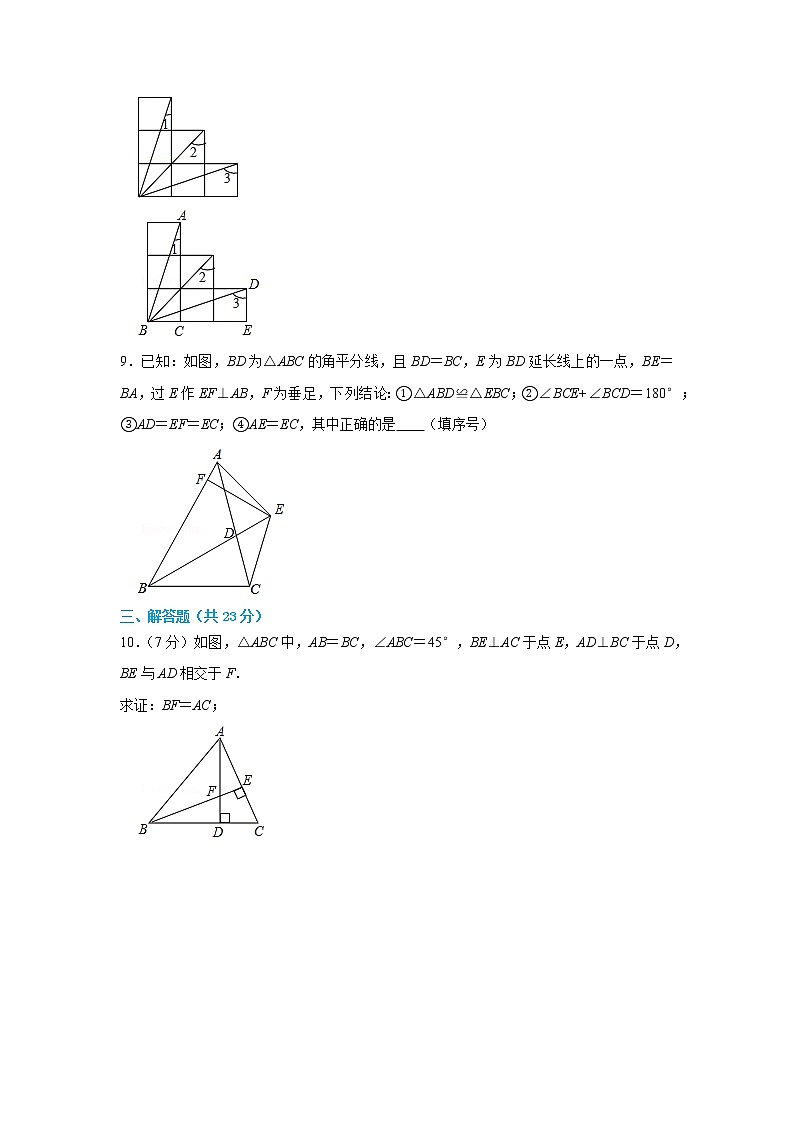
8．如图为6个边长相等的正方形的组合图形，则∠1+∠2+∠3＝　　°．

9．已知：如图，BD为△ABC的角平分线，且BD＝BC，E为BD延长线上的一点，BE＝BA，过E作EF⊥AB，F为垂足，下列结论：①△ABD≌△EBC；②∠BCE+∠BCD＝180°；③AD＝EF＝EC；④AE＝EC，其中正确的是　　（填序号）

三、解答题（共23分）

10．（7分）如图，△ABC中，AB＝BC，∠ABC＝45°，BE⊥AC于点E，AD⊥BC于点D，BE与AD相交于F．

求证：BF＝AC；

11．（8分）如图，已知点A、F、E、C在同一条直线上，AB∥CD，∠ABE＝∠CDF，AF＝CE，连结BC、AD．

（1）请直接写出图中所有的全等三角形（不添加其它的线）；

（2）从（1）中的全等三角形中任选一组进行证明．

12．（8分）如图，在直角坐标系中有一点P（5，5），M（0，m）为y轴上任意一点，N为x轴上任意一点，且∠MPN＝90°．

（1）当m＝5时，OM+ON的值为　　；

（2）当0＜m＜5时，OM+ON的值是否改变？说明你的理由；

（3）探索：当m＜0时，OM与ON的数量关系为　  

全等三角形的判定与性质参考答案

一 选择题

1．D

2．B

3．D

4．【解析】∵AD⊥BC，CE⊥AB，∴∠BEC＝∠ADB＝90°，∵∠BAD+∠B＝90°，∠BCE+∠B＝90°，∴∠BAD＝∠BCE，在△BCE和△HAE中

，

∴△BCE≌△HAE，

∴CE＝AE＝6，

∴CH＝CE﹣HE＝6﹣4＝2．

故选：B．

5．【解析】作DG⊥AB于G，DH⊥BC于H，∵D是∠ABC平分线上一点，DG⊥AB，DH⊥BC，∴DH＝DG，在Rt△DEG和Rt△DFH中，，∴Rt△DEG≌Rt△DFH（HL），

∴∠DEG＝∠DFH，又∠DEG+∠BED＝180°，∴∠BFD+∠BED＝180°，

∴∠BFD的度数＝180°﹣140°＝40°，

故选：A．

6．【解析】∵PA＝PB，∴∠A＝∠B，在△AMK和△BKN中，，

∴△AMK≌△BKN（SAS），∴∠AMK＝∠BKN，∵∠A+∠AMK＝∠MKN+∠BKN，

∴∠A＝∠MKN＝40°＝∠B，∴∠P＝180°﹣∠A﹣∠B＝180°﹣40°﹣40°＝100°，

故选：A．

二、填空题

7．（3，﹣1）　8． 135　°

9．　①②④　

【解析】①∵BD为△ABC的角平分线,∴∠ABD＝∠CBD，在△ABD和△EBC中，

，∴△ABD≌△EBC（SAS），∴①正确；

②∵BD为△ABC的角平分线，BD＝BC，BE＝BA，∴∠BCD＝∠BDC＝∠BAE＝∠BEA，

∵△ABD≌△EBC，∴∠BCE＝∠BDA，∴∠BCE+∠BCD＝∠BDA+∠BDC＝180°，∴②正确；

③∵∠BCE＝∠BDA，∠BCE＝∠BCD+∠DCE，∠BDA＝∠DAE+∠BEA，∠BCD＝∠BEA，

∴∠DCE＝∠DAE，∴△ACE为等腰三角形，∴AE＝EC，∵△ABD≌△EBC，∴AD＝EC，

∴AD＝AE＝EC，∵BD为△ABC的角平分线，EF⊥AB，而EC不垂直与BC，

∴EF≠EC，∴③错误；

④由③知AD＝AE＝EC，∴④正确；综上所述，正确的结论是①②④．故答案是：①②④．

三、解答题

10．

解：（1）AD⊥BD，∠BAD＝45°，∴AD＝BD，∵∠BFD＝∠AFE，∠AFE+∠CAD＝90°，∠CAD+∠ACD＝90°，∴∠BFD＝∠ACD，在△BDF和△ACD中，，

∴△BDF≌△ACD（AAS），∴BF＝AC；

11．

解：（1）△ABE≌△CDF，△ABC≌△CDA，△BEC≌△DFA，

（2）选△ABE≌△CDF进行证明，证明：∵AB∥CD，∴∠BAE＝∠DCF，

∵AF＝CE，∴AF+EF＝CE+EF，即AE＝CF．在△ABE和△CDF中，

∴△ABE≌△CDF（AAS）．若选另两对证明如下：∵△ABE≌△CDF，∴AB＝DC，

∵AB∥CD，∴∠BAC＝∠DCA，在△ABC和△CDA中

∴△ABC≌△CDA（SAS）．∴AD＝CB，∠ACB＝∠CAD，

∵AF＝CE，∴△AFD≌△CEB（SAS）．

12．

解：（1）作PA⊥y轴于A，PB⊥x轴于B，如图1所示：∵P（5，5），

∴PA＝PB＝OA＝OB＝5，∴A（0，5），当m＝5时，M（0，5），

∴A与M重合，B与N重合，∴ON＝OH＝5，∴OM+ON＝10；故答案为：10；

（2）当0＜m＜5时，OM+ON的值不改变，理由如下：

作PA⊥y轴于A，PB⊥x轴于B，如图2所示：

则∠APB＝90°，PA＝PB＝5，

∵∠MPN＝90°，

∴∠APM＝∠BPN，

在△APM和△BPN中，，

∴△APM≌△BPN（ASA），

∴AM＝BN，

∴OM+ON＝OA﹣AM+OB+BN＝OA+OB＝10；

（3）当m＜0时，OM与ON的数量关系为OM＝ON﹣10，理由如下：

作PA⊥y轴于A，PB⊥x轴于B，如图3所示：

同（2）得：△APM≌△BPN（ASA），

∴AM＝BN，

∴OM＝AM﹣OA＝BN﹣OA＝ON﹣OB﹣OA＝ON﹣10；

故答案为：OM＝ON﹣10．