2022-2023人教版八年级数学上册重难题型全归纳及技巧提升专项精练 第一次月考押题预测卷（考试范围：第十一、十二章）（原卷+解析卷）

第一次月考押题预测卷

（考试范围：第十一、十二章）

姓名：__________________     班级：______________   得分：_________________

注意事项：

本试卷满分120分，考试时间90分钟，试题共26题．答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置．

一、选择题（本大题共10小题，每小题3分，共30分）在每小题所给出的四个选项中，只有一项是符合题目要求的．

1．（2022·四川凉山·八年级期末）下列命题是真命题的是（       ）

A．等底等高的两个三角形全等 B．周长相等的直角三角形都全等

C．有两边和一角对应相等的两个三角形全等 D．有一边对应相等的两个等边三角形全等

2．（2022·四川成都·八年级期末）生活中常用各种正多边形地砖铺砌成美丽的图案．用形状、大小完全相同的一种或几种平面图形进行拼接，彼此之间不留空隙、不重叠地铺成一片，就是平面图形的镶嵌．下列图形中不能与正三角形镶嵌整个平面的是（　　）

A．正方形 B．正五边形 C．正六边形 D．正十二边形

3．（2022·四川省成都市七中育才学校七年级期中）如图，在ABC中，AD是BC边上的中线，BE是ABD中AD边上的中线， 若=24，则ABE的面积是（       ）

A．4 B．12 C．6 D．8

4．（2022·江苏南京·七年级期中）如图，用四颗螺丝将不能弯曲的木条围成一个木框，不计螺丝大小，其中相邻两颗螺丝的距离依次为3、4、6、8，且相邻两根木条的夹角均可以调整，若调整木条的夹角时不破坏此木框，则任意两颗螺丝的距离的最大值是(     )

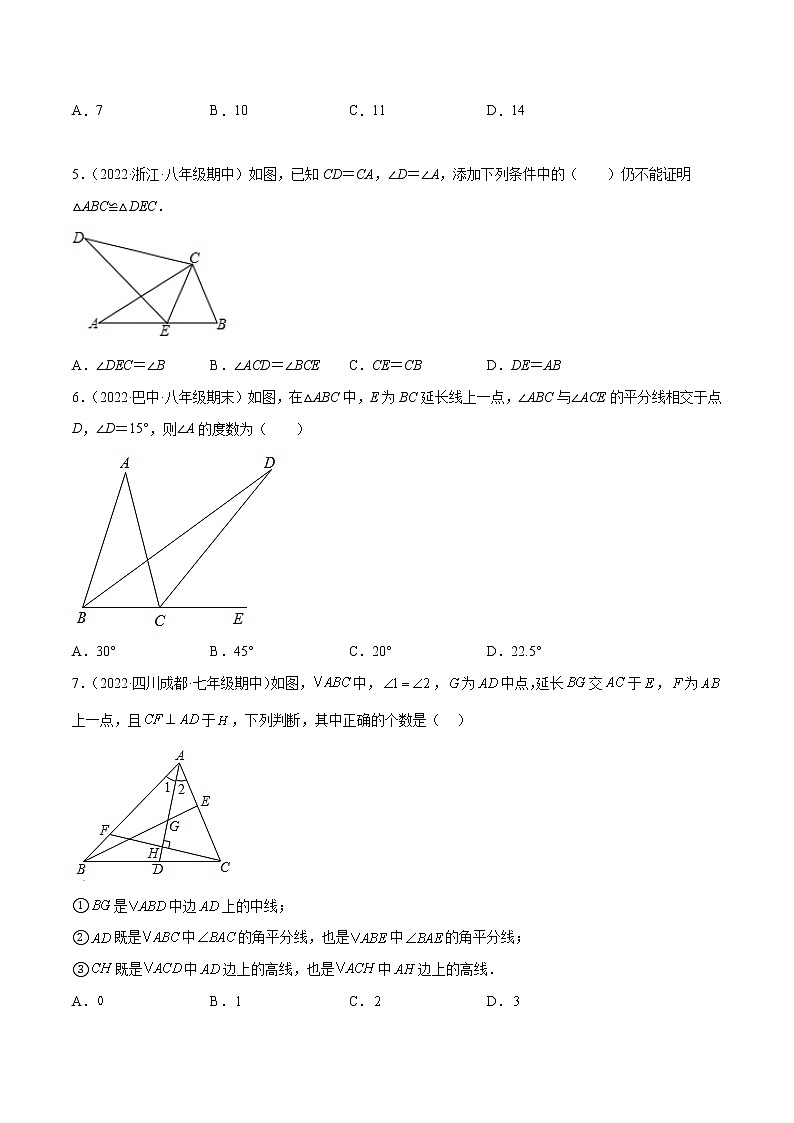
A．7 B．10 C．11 D．14

5．（2022·浙江·八年级期中）如图，已知CD＝CA，∠D＝∠A，添加下列条件中的（　　）仍不能证明△ABC≌△DEC．

A．∠DEC＝∠B B．∠ACD＝∠BCE C．CE＝CB D．DE＝AB

6．（2022·巴中·八年级期末）如图，在△ABC中，E为BC延长线上一点，∠ABC与∠ACE的平分线相交于点D，∠D＝15°，则∠A的度数为（　　）

A．30° B．45° C．20° D．22.5°

7．（2022·四川成都·七年级期中）如图，中，，为中点，延长交于，为上一点，且于，下列判断，其中正确的个数是（   ）

①是中边上的中线；

②既是中的角平分线，也是中的角平分线；

③既是中边上的高线，也是中边上的高线．

A． B． C． D．

8．（2022·四川·广汉市八年级期中）如图，将△ABC纸片沿DE折叠，使点A落在点A'处，且A'B平分∠ABC，A'C平分∠ACB，若∠BA'C＝120°，则∠1+∠2的度数为（　　）

A．90° B．100° C．110° D．120°

9．（2022·广东·八年级月考）如图，在△ABC中，∠C＝90°，AD平分∠BAC，DE⊥AB于E，下列结论：①；②；③∠BDE＝∠BAC；④BE＝DE；⑤，其中正确的个数为（ ）

A．5个 B．4个 C．3个 D．2个

10．（2022·四川·江油八年级阶段练习）如图，已知等边和等边，点P在的延长线上，的延长线交于点M，连接；下列结论：①；②；③平分；④，其中正确的有（       ）．

A．①③④ B．①② C．②③④ D．①②③④

二、填空题（本大题共8小题，每小题3分，共24分．不需写出解答过程，请把答案直接填写在横线上）

11．（2022·巴中·七年级期末）如图所示，王师傅做完门框为防止变形，在门上钉上AB、CD两条斜拉的木条，其中的数学原理是________．

12．（2022·河北邯郸·七年级期末）如图是可调躺椅示意图（数据如图），AE与BD的交点为C，且∠A，∠B，∠E保持不变．为了舒适，需调整∠D的大小，使，则图中∠D应___（填“增加”或“减少”）___度．

13．（2022·河北·八年级专题练习）如图，锐角△ABC中，D，E分别是AB，AC边上的点，△ADC≌△ADC′，△AEB≌△AEB′，且C′D∥EB′，BE，CD交于点F．若∠BAC＝40°，则∠BFC的度数为 _____．

14．（2022·山东青岛·七年级期末）如图，已知AD平分∠BAC，要使．只需再添加一个条件就可以了，你选择的条件是______，理由是_______．

15．（2022·四川·达州中学七年级期中）中，若，为三条内角角平分线的交点，则__________度．

16．（2022·河北廊坊·八年级期末）在方格纸中，每个小方格的顶点叫做格点，以格点的连线为边的三角形叫做格点三角形，解决下列问题．

（1）如图1，以点D和点E为两个顶点作格点三角形，使所作的格点三角形与△ABC全等，那么这样的格点三角形最多可以画出_______个；（2）如图2，∠1＋∠2＝_______．

17．（2022·西安市七年级模拟）如图，△ABC的面积是21，点D、E、F分别在边BC、AB、

AC上，且AE＝2，EB＝4．若△ABD与四边形DFEB面积相等，则△ADC的面积＝_____．

18．（2022·成都市七中育才学校七年级期中）如图，AD⊥BC于点D，BE⊥AC于点E，AD与BE交于点O，连接CO并延长交AB于点F，延长AD至点G，若GE平分∠DGC，CE平分∠DCH，则下列结论：①∠ABE＝∠ACF；②∠GEB＝45°；③EO＝EC；④AE﹣CE＝BF；⑤AG﹣CG＝BC，其中正确的结论有______（写序号）．

三、解答题（本大题共8小题，共66分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤）

19．（2022·福建·八年级阶段练习）如图，在△ABC中，∠BAC是钝角，完成下列画图．（不必尺规作图）

（1）∠BAC的平分线AD；（2）AC边上的中线BE；（3）AC边上的高BF．

20．（2022·江西上饶·八年级期末）如图，已知五边形ABCDE的各边都相等，各内角也都相等，点F、G分别在边BC、CD上，且FC=GD．(1)求证：ΔCDF ≌ ΔDEG；(2)求∠EHF的大小．

21．（2022·湖南·八年级阶段练习）如图，在△ABD中，∠ABC=45°，AC，BF为△ABD的两条高，CM//AB，交AD于点M；求证：BE=AM+EM．

22．（2022·成都·八年级期末）如图，在中，，，将点沿着线段翻折，使点落在边上的点处．(1)求的度数；(2)求的度数．

23．（2022·湖北）（1）模型：如图1，在中，平分，，，求证：．

（2）模型应用：如图2，平分交的延长线于点，求证：．

（3）类比应用：如图3，平分，，，求证：．

24．（2022·陕西渭南·七年级期末）问题情境：（1）如图1，，OC平分∠AOB，把三角尺的直角顶点落在OC的任意一点P上，并使三角尺的两条直角边分别与OA、OB相交于点E、F，过点P作于点N，作于点M，请写出PE与PF的数量关系______．

变式拓展：（2）如图2，已知OC平分∠AOB，P是OC上一点，过点P作于M，于N，PE边与OA边相交于点E，PF边与射线OB的反向延长线相交于点F，．试解决下列问题：

①PE与PF之间的数量关系还成立吗？为什么？②若，试判断OE、OF、OP三条线段之间的数量关系，并说明理由．

25．（2022·遂宁·八年级期末）问题情境：如图①,在直角三角形ABC中,∠BAC=90∘,AD⊥BC于点D,可知：∠BAD=∠C(不需要证明)；

(1)特例探究：如图②,∠MAN=90∘,射线AE在这个角的内部,点B．C在∠MAN的边AM、AN上,且AB=AC,CF⊥AE于点F,BD⊥AE于点D．证明：△ABD≌△CAF；

(2)归纳证明：如图③,点B,C在∠MAN的边AM、AN上,点E,F在∠MAN内部的射线AD上,∠1、∠2分别是△ABE、△CAF的外角．已知AB=AC,∠1=∠2=∠BAC．求证：△ABE≌△CAF；

(3)拓展应用：如图④，在△ABC中，AB=AC，AB>BC．点D在边BC上，CD=2BD，点E.F在线段AD上，∠1=∠2=∠BAC．若△ABC的面积为18，求△ACF与△BDE的面积之和是多少?

26．（2021·四川八年级期末）如图1，在等边三角形中，于于与相交于点．（1）求证：；（2）如图2，若点是线段上一点，平分交所在直线于点．求证：．（3）如图3，若点是线段上一点（不与点重合），连接，在下方作边交所在直线于点．猜想：三条线段之间的数量关系，并证明．