黑龙江省哈尔滨市德强中学2022-2023学年九年级上学期9月月考数学试卷(含答案)

哈尔滨德强学校2022-2023学年度(上)

9月份线上教学问题诊断

九年级数学学科

(分值：120分   总时间：120分钟)

一、选择题(每小题3分，共计30分)

1.-5的相反数是().

A.         B.      C.5     D.-5

2.下列运算一定正确的是().

A.      B.       C.       D.

3.下列图形中，不是轴对称图形的是()

A.    B.    C.    D.

4.如图所示的几何体是由六个小正方体组合而成的，它的俯视图是().

A.   B.   C.   D.

5.把抛物线向左平移1个单位，然后向上平移3个单位，则平移后抛物线为().

A.   B.   C.  D.

6.方程解是().

A.x=5      B.      C.      D.x=4

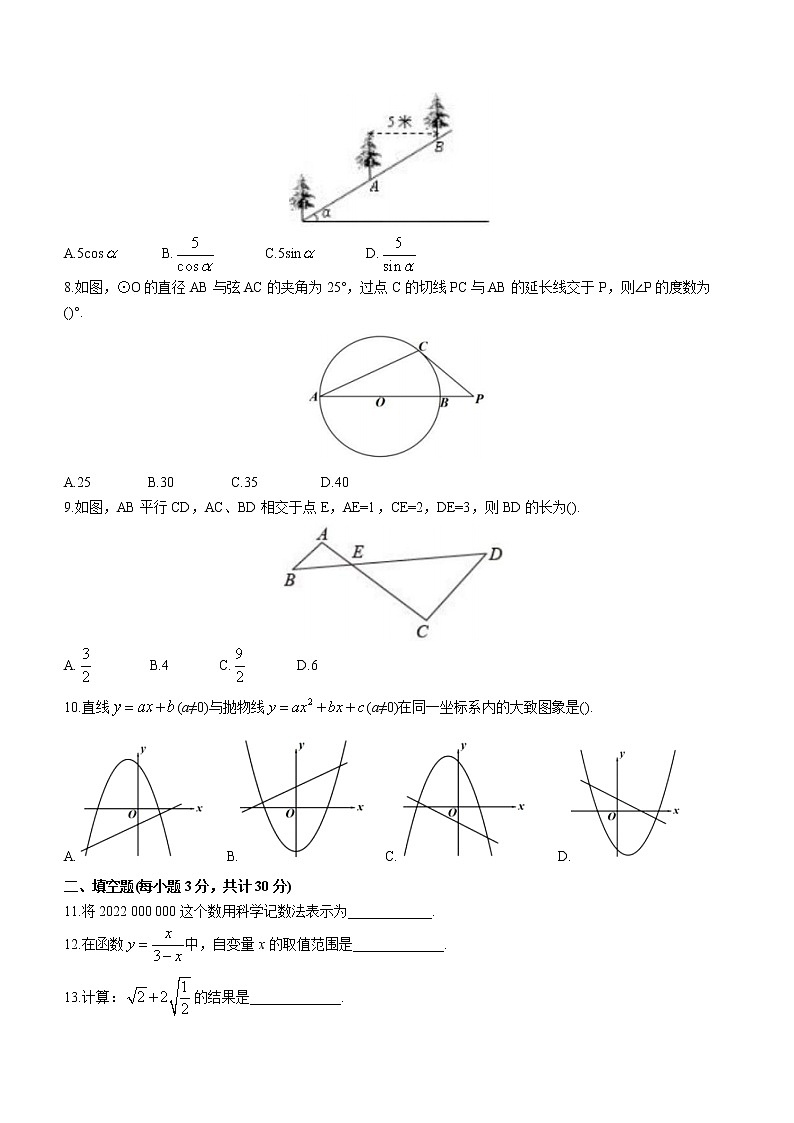
7.如图，在坡角为的山坡上栽树，要求相邻两树之间的水平距离为5米，那么这两树在坡面上的距离AB为().

A.5cos      B.       C.5sin       D.

8.如图，⊙O的直径AB与弦AC的夹角为25°，过点C的切线PC与AB的延长线交于P，则∠P的度数为()°.

A.25        B.30        C.35         D.40

9.如图，AB平行CD，AC、BD相交于点E，AE=1，CE=2，DE=3，则BD的长为().

A.        B.4       C.       D.6

10.直线(a≠0)与抛物线(a≠0)在同一坐标系内的大致图象是().

A.   B.   C.    D.

二、填空题(每小题3分，共计30分)

11.将2022 000 000这个数用科学记数法表示为____________.

12.在函数中，自变量x的取值范围是_____________.

13.计算：的结果是_____________.

14.把多项式分解因式的结果是____________.

15.不等式组的解集为____________.

16.己知抛物线的解析式为，则该抛物线与y轴的交点坐标为_____________.

17.一个扇形的面积为12πcm2，半径为6cm，则此扇形的圆心角是____________度.

18.在△ABC中，AB=AC=4，S△ABC=，则tan∠ACB=_____________.

19.如图，△ABC是⊙O的内接三角形，CD⊥AB于点D，若AD=3，BC=10，CD=6，则⊙O的半径为____________.

20.如图，在△ABC中，∠ACB=90°，tan∠ABC=，点D为AB上一点，连接CD，过A作AE⊥CD于E，AE=，连接BE，若S△BCE=18，则BD的长为_____________.

三、解答题(其中21-22题各7分，23-24题各8分，25-27题各10分，共计60分)

21.先化简，再求代数式的值，其中a=tan60°-2sin30°.

22.如图，在每个小正方形的边长均为1的方格纸中，有线段AB和线段CD，点A、B、C、D均在小正方形的项点上.

(1)在方格纸中画以AB为斜边的等腰直角△ABE；

(2)在方格纸中画以CD为一边的△CDF，点F在小正方形的顶点上，且△CDF的面积为5，tan∠DCF=，连接EF，并直接写出线段EF的长.

23.为了解学生线上学习的需求，某校随机对本校的部分学生进行了“你对哪类在线学习方式最感兴趣”的调查，并根据调查结果，绘制成如下两幅统计图.根据图中信息，解答下列问题：

(1)求本次调查的学生总人数：

(2)通过计算补全条形统计图；

(3)该校共有学生2100人，请你估计该校对“在线阅读”最感兴趣的学生人数.

24.如图，在四边形ABCD中，AD∥BC，AC平分∠BAD，BD平分∠ABC.

(1)如图1，求证：四边形ABCD是菱形；

(2)如图2，过点D作DE⊥BD交BC延长线于点E，在不添加任何辅助线的情况下，请直接写出图2中所有与△CDE面积相等的三角形(△CDE除外).

25.某超市有甲、乙两种商品，若买1件甲商品和4件乙商品，共需130元；若买2件甲商品和3件乙商品，共需135元.

(1)求甲、乙两种商品每件售价分别是多少元?

(2)甲商品每件的成本是20元，根据市场调查：若按(1)中求出的单价销售，该超市每天销售甲商品100件，若销售单价每上涨1元，甲商品每天的销售量就减少5件.求甲商品每件售价为多少元时，甲商品每天的销售利润最大，最大利润是多少?

26.在⊙O中，弦AB、CD相交于点P，且.

(1)如图1，求证：AB=CD；

(2)如图2，点M、N分别为弦AB、CD的中点，连接OM、ON，且∠MON=90°，求证：AB⊥CD；

(3)如图3，在(2)的条件下，连接AC、CM，CM交ON于点E，过点M作FM⊥CM交AC于点F，FM：EM=3：2，CE-EM=10，求AF的长.

27.如图，在平面直角坐标系中，点O为坐标原点，抛物线与x轴的负半轴交于点A，与x的正半轴交于点B，与y轴正半轴交于点C，OB==2OA.

(1)求抛物线的解析式；

(2)点D是第四象限内抛物线上一点，连接AC、CD、AD，AD交y轴于点E，CD交x轴于点F，设△ACD的面积为S，点D的横坐标为t，求S与t的函数关系式(不要求写自变量t的取值范围)；

(3)在(2)的条件下，点M在OC上，点N在OB上，连接BM、CN交于点P，点Q在MB上，连接CQ、NQ，若∠CAB=∠BAE+∠ACO，OM：OE=12：5，CM=ON，∠MCQ=∠BPN，求NQ的长.

德强中学九(上)数学2022年10月月考真题答案

一、选择题：

二、填空题：

11.2.022×109；12.x≠3；13.；14.m(n－3)(n＋3)；15.；16.(0，－3)；17.120；

18.或；19.；20..

21.解：原式=

当a=tan60°－2sin30°=时，

原式=.

22.(1)如右图所示：

(2)EF=.

23.解：(1)18÷20%=90(人)

答：本次调查的学生总人数为90人。

(2)90－24－18－12=36(人)

(3)24÷90×100%×2100=560(人)

答：我估计该校对“在线阅读”最感兴趣的学生有560人。

24.解：(1)∵AC平分∠BAD，

∴∠BAO=∠DAO，

∵AD∥BC，

∴∠BCA=∠DAO=∠BAO，

∵BD平分∠ABC，

∴∠ABO=∠CBO，

∵OB=OB，

∴△AOB≌△COB，

∴AB=BC，

∴∠ADB=∠CBD=∠ABD，

∵AO=AO，

∴△AOD≌△AOB，

∴AD=AB=BC，

∵AD∥BC，

∴四边形ABCD是平行四边形，

∴四边形ABCD是菱形

(2)△BCD、△BAD、△ACD、△ACB

25.解：(1)设甲种商品每件售价是x元，乙种商品每件售价是y元，

，

∴

答：橙甲种商品每件售价是30元，乙种商品每件售价是25元。

(2)设甲商品每件售价为m元时，每天的销售利润为n元，

n=(m－20)100－5(m－20)

=－5m2＋350m－5000

=－5(m－35)2＋1125

∵a=－5＜0，

∴开口向下，

∴当m=35时，n有最大值，

N最大=1125(元)

答：汁甲商品每件售价为35元时，

甲商品每天的销售利润最大，最大利润是1125元。

26.解：(1)∵，，

∴，

∴AB=CD，

(2)∵M为弦AB中点，

∴OM平分AB，

∵O为圆心，AB不是直径，

∴OM⊥AB，

∵N为弦CD中点，

∴ON平分CD，

∵O为圆心，CD不是直径，

∴ON⊥CD，

∴∠OMP=∠ONP=90°，

又∵∠MON=90°，

在四边形OMPN中，

∠OPM=360°－∠OMP－∠MON－∠ONP=360°－90°－90°=90°，

∴AB⊥CD

(3)∵，

∴∠ACP=∠CAP，

∵∠APC=90°，

∴∠A＋∠ACP=90°，∴∠A==45°，

∴AP=CP，

∵M为AB中点，N为CD中点，

∴AM=AB，CN=CD，

∵AB=CD，

∴AM=CN，

∴PA－AM=CP－CN，

∴PM=PN，

过F作FK⊥OM于K，

∴∠FKM=∠MOE=90°，

在Rt△FMK中，∠MFK＋∠FMK=90°，

∵FM⊥CM，

∴∠CMF=90°，

∴∠FMK＋∠CMK=90°，

∴∠MFK=∠CMO，

∴△FMK∽△MEO，

∴

设KM=3y，OE=2y，OM=ON=2x，FK=3x，

过F作FS⊥AP于S，

∴四边形FSMK是矩形，

∴FS=MK=3y，MS=FK=3x，

在Rt△AFS中，∠AFS=90°，∠A=90°，

∴∠A=∠AFS，

∴AS=FS=3y，

∴CN=AM=AS＋MS=3x＋3y，EN=ON－OE=2x－2y，

∴∠MON=∠CNE=90°，∠OEM=∠CEN，

∴△OEM∽△CEN，

∴，，x1=3y，(舍)，

∴EN=4y，

设EM=z，CE=z＋10，

∴，

∴，z=10，

∴EM=10，FM=15，

在Rt△OEM中，tan∠OME=，

∵FK∥AM，

∴∠AMF=∠KFM=∠OME，

∴tan∠AMF=∠FSM=90°，

在Rt△FSM中，tan∠AMF=，，设FS=a，MS=3a，

勾股得，解得，(舍)，

∴FS=，

在Rt△ASF中，sinA=，

∴AF=

27.解：(1)∵抛物线交x轴负半轴于A，

x正半轴于B，交y轴正半轴于C，

当y=0时，x1=－2，x2=m，

∴A(－2，0)，B(m，0)，

∴OA=2，OB=2OA=4，

∴B(4，0)

∴m=4，

∴抛物线的解析式

(2)当x=0时，y=3，

∴C(0，3)，OC=3，

过D作DK⊥x轴于K，过D作DI⊥y轴于I，

∵OI⊥OK，

∴四边形OIDK为矩形，

∵D的横坐标为t且在抛物线上，

∴D(t，)，

∴OK=t，

∴OI=DR=

∵∠AOE=∠AKD=90°，∠KAD=∠KAI，

∴△AOE∽△AKD，

∴，

∴，OE=，

∴CE=OC+OE=，

S=S△ACE＋S△CDE=

=

(3)在OC上取一点S使AS=AE，

∴设∠ACO=m，

在Rt△AOC中，∠CAO=90°－∠ACO=90°－m，

∴∠OAE=∠CAO－∠ACO=90°－2m，

在Rt△AOE中，∠AEO=90°－∠OAE=2m，

∴∠ASO=∠AEO=2m，

∴∠CAS=∠ASO－∠ACO=m，

∴∠CAS=∠ACS，

∵AO⊥SE，

∴OS=OE=，

∴CS=AS=OC－OS=，

∴

解得，

∴OE=，

∴OM=OE×=2，

∴CM=OC－OM=3－2=1，

∴ON=CM=1，

∴N(1，0)，M(0，2)，

设CN解析式为y=kx＋b，

，

∴y=－3x＋3，

设BM解析式为y=k'x＋b'，

，，

∴

∴CN于BM交于P，

∴，解得，

∴P，

过P作PK⊥OC于N，

∴K(0，)

∴MK=2－，PK=，

∴在Rt△MKP中，∠MKP=90°，

∴MP=，

∴∠CPM=∠BPN=∠MCQ，∠CMP=∠CMQ，

∴△CMP∽△QMC，

∴，

∴QM=，

在Rt△BOM中，BM=，tan∠OBM=，

∴BQ=BM－QM=，

过Q作QW⊥BO于W，

在Rt△QWB中，∠QWB=90°，tan∠OBM=，

设QW=b，BW=2b，

，b1=1，b2=－1(舍)，

∴BW=2，QW=1，

∴NW=BO－ON－BW=4－1－2=1，

∴在Rt△QNW中，∠QWN=90°，

勾股得QN=.