






人教版八年级上册数学 期中复习 优质课件
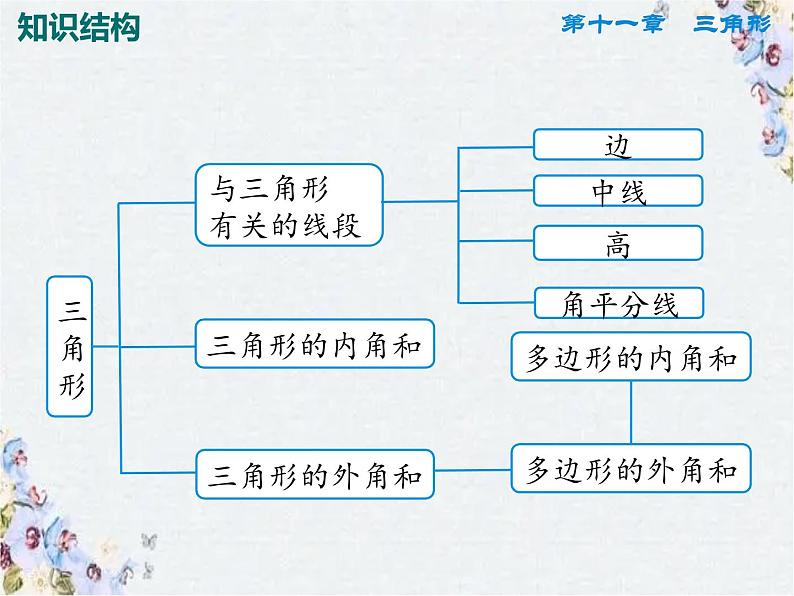
展开第十一章 三角形
三角形两边之和大于第三边,三角形两边之差小于第三边.
2.三角形的高、中线、角平分线的定义
从三角形的一个顶点向它所对的边所在直线画垂线,顶点与垂足之间的线段叫做三角形的这条边上的高.连接三角形的一个顶点和它所对的边的中点,所得线段叫做三角形这条边上的中线.
三角形一个内角的平分线与这个角的对边相交,这个角的顶点和交点之间的线段叫做三角形的角平分线.
三角形的三条中线的交点叫做三角形的重心.
三角形具有稳定性,四边形具有不稳定性.
1.三角形的内角和定理
三角形三个内角的和等于180°.
直角三角形的两个锐角互余.有两个角互余的三角形是直角三角形.
3.三角形内角和定理的推论
三角形的外角等于与它不相邻的两个内角的和.
4.三角形外角和的性质
三角形的外角和等于360°.
1.多边形和正多边形的定义
在平面内,由一些线段首尾顺次相接组成的封闭图 形叫做多边形.各个角都相等,各个边都相等的多边形叫做正多边形.
n边形的内角和等于(n-2)×180°.
多边形的外角和等于360°.
例1 如图,三角形纸片ABC中,A=65°,∠B=75°,将纸片的一角折叠,使点C落在△ABC内,若∠1=20°,则∠2的度数为 。
例2 在绿茵场上,足球队带求进攻,总是向球门AB冲近,说明这是为什么?
解:如图,设球员接球时位于点C,他尽力向球门冲近到D,此时不仅距离球门近,射门更有力,而且对球门AB的张角也扩大,球更容易射中,理由说明如下:延长CD到E,则∠ADE>∠ACE,∠BDE>∠BCE,所以∠ADE+∠BDE>∠ACE+∠BCE,即∠ADB>∠ACB.
例3 已知一个等腰三角形的三边长分别为x,2x-1,5x-3,求其周长.
解:(1)若x=2x-1,则x=1,此时三边为1,1,2,因为1+1=2,不符合三角形三边关系,舍去。 (2)若x=5x-3,x=(3/4)。此时三边为(3/4),(1/2),(3/4),符合三角形三边关系,周长为(3/4)+(1/2)+(3/4)=2 (3)若2x-1=5x-3,x=(2/3)。此时三边为(2/3),(1/3),(1/3),因为(1/3)+(1/3)=(2/3),所以不符合三角形三边关系,舍去综上,此等腰三角形的周长为2.
例4 如图,D、E为△ABC内的两点,试说明AB+AC>BD+DE+EC.
证明:延长BD交AC于点P,延长CE交BP于点F.在△ABP中,AB+AP>BP=BF+PF.在△PFC中,FP+PC>FC=FE+EC.∴AB+AP+FP+PC>BF+PF+EF+EC.即AB+AC>BF+EF+EC=BD+DF+EF+EC.在△FDE中,DF+EF>DE,∴BD+DF+EF+EC>BD+DE+EC.即AB+AC>BD+DE+EC.
例5 如图,在锐角△ABC中,CD、BE分别是AB、AC边上的高,且CD、BE交于一点P,若∠A=50°,则∠BPC的度数是( )
A.150° B.130° C.120° D.100°
例6 如图所示,BE与CD相交于点A,CF为∠BCD的平分线,EF为∠BED的平分线。(1)试探求∠F与∠B、∠D间有何等量关系。
(2)EF与FC能垂直吗?说明理由.
(3)若∠B:∠D:∠F=2:x:3,求x的值.
解:(1)∠D+∠B=2∠F∵EF平分∠BED,CF平分∠BCD∴∠DEF=(1/2)DEB,∠FCD=(1/2)∠BCD而∠EMC=∠D+(1/2)∠BED, ∠EMC=∠F+(1/2)∠BCD∴∠D+(1/2)∠BED=∠F+(1/2)∠BCD ① 同理可得:∠B+(1/2)∠BCD=∠F+(1/2)∠BED ② ①+②得:∠D+∠B=2∠F.
(2)能,若EF与FC垂直,即∠F=90°,则∠B+∠D=180° ,也就是说,如果∠D与∠B互补,则EF⊥FC.
(3) ∵∠B:∠D:∠F=2:x:3 , ∴设∠B=2m,∠D=xm,∠F=3m , 由(1)得xm+2m=2×3m ∴x=4.
例7 阅读下面的问题及解答: 如图(1),△ABC中∠ABC、∠ACB的角平分线交于O点,如图(2),△ABC 中∠ABC、∠ACB的三等分线交于O1、O2,则∠BO1C=(2/3)×180°+(1/3)∠A,∠BO2C=(1/3)×180°+(2/3)×∠A。根据以上信息:
(1)你能猜想出它的规律? n等分时[内部有(n-1)个点, ∠BO1C= , ∠BOn-1C= (用含n的代数式表示)
(2)根据你的猜想,当n=4时说明∠BO3C的度数成立.
解:(1)当n=2时,∠BOC=(1/2)×180°+(1/2)∠A, 当n=3时,∠BO1C=(2/3)×180°+(1/3)∠A,∠BO2C=(1/3)×180°+(2/3)∠A。
由此可见,系数分母即是n,∠BO1C的系数的第一个分子是n-1,第二个分子是1.由此可猜想∠BO1C=(n-1/n)×180°+(1/n)∠A。同理:∠BOn-1C=(1/n)×180°+(n-1/n)∠A。
(2)当n=4时,代入所猜想的公式得∠BO3C=(1/4)×180°+(3/4)×∠A。 另外,在△BO3C中由三角形内角和定理得: ∠BO3C=180°-(∠O3BC+∠O3CB) =180°-(3/4)(∠ABC+∠ACB) =180°-(3/4)(180°-∠A) =(1/4)×180°+(3/4)∠A 结果与猜想一致。
例8 求证:两条平行线被第三条直线所截得的一组同旁内角的平分线互相垂直。
已知:如图,AB∥CD,EF交AB与于E,EM平分∠BEF,FN平分∠DFE,EM与FN交于G。求证:EM⊥FN.
证明:∵AB∥CD ∴∠BEF+∠DFE=180° ∵EM平分∠BEF,FN平分∠DFE, ∴∠1+∠2=(1/2)(∠BEF+∠DFE) =(1/2)×180°=90° ∴∠EGF=180°-(∠1+∠2)=90° ∴EM⊥FN
解:设原多边形是n边形,分两种情况讨论: (1)若截取不经过多边形的另一个顶点,则新多边形仍是n边形(如图(1)) 由题设得:(n-2).180°=2520°,解得n=16° (2)若截线经过多边形的顶点,则新多边形(n-1)边形(如图(2)), 由题设得:(n-1-2).180°=2520°,解得:n=17 综上:n=16或17
例9 如图,∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠K的度数是多少?
【解析】如图,设AK与GH交于点M,GF与DE交于点N,连接AG,GD.在△MAG与△MHK中,∵∠AMG=∠HMK,∴∠MAG+∠MGA=∠H+∠K.同理可得,∠NGD+∠NDG=∠E+∠F.∴∠BAK+∠B+∠C+∠CDE+∠E+∠F+∠MGN+∠H+∠K=∠BAK+∠MAG+∠MGA+∠MGN+∠NGD+∠NDG+∠CDE+∠C+∠B=∠BAG+∠AGD+∠GDC+∠C+∠B=(5-2)×180°=540°.
第十二章 全等三角形
1:什么是全等三角形?一个三角形经过哪些变化可以得到它的全等形?
2:全等三角形有哪些性质?
能够完全重合的两个三角形叫做全等三角形。 一个三角形经过平移、翻折、旋转可以得到它的全等形。
(1)全等三角形的对应边相等、对应角相等。(2)全等三角形的周长相等、面积相等。(3)全等三角形的对应边上的对应中线、角平分线、高线分别相等。
边边边:三边对应相等的两个三角形全等(可简写成“SSS”)边角边:两边和它们的夹角对应相等两个三角形全等(可简写成“SAS”)角边角:两角和它们的夹边对应相等的两个三角形全等(可简写成“ASA”)角角边:两角和其中一角的对边对应相等的两个三角形全等(可简写成“AAS”)斜边.直角边:斜边和一条直角边对应相等的两个直角三角形全等(可简写成“HL”)
角的内部到角的两边的距离相等的点在角的平分线上。
用法: ∵ QD⊥OA,QE⊥OB,QD=QE.∴点Q在∠AOB的平分线上.
角的平分线上的点到角的两边的距离相等.
用法:∵ QD⊥OA,QE⊥OB,点Q在∠AOB的平分线上∴ QD=QE.
二.角的平分线:1.角平分线的性质:
学习全等三角形应注意以下几个问题:
(1)表示两个三角形全等时,表示对应顶点的字母要写在对应的位置上;
(2)时刻注意图形中的隐含条件,如 “公共角” 、“公共边”、“对顶角”
第十三章 轴对称
例1 下列说法中,正确的个数是( )①轴对称图形只有一条对称轴②轴对称图形的对称轴是一条线段③两个图形成轴对称,这两个图形是全等图形④全等的两个图形一定成轴对称⑤轴对称图形是指一个图形,而成轴对称是指两个图形 A. 1个 B. 2个 C. 3个 D. 4个
例2 下列图案是轴对称图形的有( ) A.1个 B.2个 C. 3个 D.4个例3 等腰三角形的对称轴有( ) A. 1条 B. 3条 C. 1条或3条 D.无数条
例4 如图,有A,B,C三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在( )A. 在AC,BC两边高线的交点处B. 在AC,BC两边中线的交点处C. 在AC,BC两边垂直平分线的 交点处D. 在∠A,∠B两内角平分线的 交点处
解:∵DE是AC的垂直平分线∴AD=CD,CE=AE=5 cm∴AC=AE+CE=10 cm∵△CBD的周长为24 cm∴BC+CD+BD=BC+AD+BD=BC+AB=24(cm)∴△ABC的周长为AC+AB+BC=10+24=34(cm)
例5 如图,在△ABC中,DE是AC的垂直平分线,垂足为E,交AB于点D,AE=5cm,△CBD的周长为24cm.求△ABC的周长.
证明:连接AF.∵AB=AC,∠BAC=120°∴∠B=∠C=30°∵EF为AB的垂直平分线 ∴BF=AF ∴∠BAF=∠B=30°∴∠FAC=120°-30°=90°∵∠C=30° ∴CF=2AF∵BF=AF ∴FC=2BF
例6 如图,在△ABC中,AB=AC,∠BAC=120°,EF为AB的垂直平分线,EF交BC于点F,交AB于点E.求证:FC=2BF.
例7 已知等腰三角形的一个内角是70°,则它的另外两个内角度数分别是 .例8 已知等腰三角形的一个内角是100°,则它的另外两个内角度数分别是 .例9 已知等腰三角形有两边的长分别为8,4,则这个等腰三角形的周长是 .例10 等腰三角形一腰上的高与另一腰的夹角为30°,则它的顶角度数为 .
55°,55°或 70°,40°
例11 如图,已知P,Q是△ABC边BC上的两点,且BP=PQ=QC=AP=AQ.求∠BAC的度数.
解:∵AP=PQ=AQ∴∠APQ=∠AQP=∠PAQ=60°∵AP=BP ∴∠B=∠PAB∵∠APQ=∠B+∠PAB=60°∴∠B=∠PAB=30°同理得 ∠QAC=30°∴∠BAC=∠PAB+∠PAQ+∠QAC =30°+60°+30°=120°
例12 如图,点O是线段AD的中点,分别以AO和DO为边在线段AD的同侧作等边三角形OAB和OCD,连接AC和BD,相交于点E,连接BC.求∠AEB的大小.
解:∵△OAB和△ODC都是等边三角形,且点O是线段AD的中点.∴OD=OC=OB=OA,∴∠1=∠2=60°,∠4=∠5,又∵∠4+∠5=∠2=60°,∠4=30 ° ,同理,∠6=30°,∴∠AEB=∠4+∠6=60°.
例13 在平面直角坐标系中,点P(-2,1)关于y轴对称的点的坐标为 ,点P(-2,1)关于x轴对称的点的坐标为 .例14 如图,求△ABC的顶点A,B,C关于y轴对称的点的坐标.
解:点A,B,C的坐标分别是A(-3,2),B(-4,-2),C(-2,-3),因为点(x,y)关于y轴对称点的坐标为(-x,y),所以点A,B,C关于y轴对称点的坐标分别是A'(3,2),B'(4,-2),C'(2,-3).
例15 如图,在方格纸上建立平面直角坐标系,线段AB的两个端点都在格点上,直线MN经过坐标原点.写出点A的坐标 ,B的坐标 .利用尺规作出线段AB关于直线MN的对称图形(保留作图痕迹,不写作法).
例16 如图,要给A,B两镇供气,泵站修在管道的什么地方,可使所用的输气管线最短?
解:如图,作A关于燃气管道m(第一条线)的对称点C.连接BC交燃气管道m于点P,则点P为所求,即要在燃气管道m上修建一个泵
站,分别向A,B两镇供气,泵站修在管道的点P处,可使用所用的输气管线最短.
例17 如图,河流 l 两旁有两个村庄A,B,现要在河边修一个水泵站,同时向A,B两村供水,问水泵站修在什么地方才能使所铺设的管道最短?试在图中标出水泵站(用点P表示)的位置,并说明这样做的理由.
解:如图,连接AB,交河边于点P,则点P即为所求.理由:两点之间,线段最短.
初中数学人教版八年级上册15.2.1 分式的乘除教学演示ppt课件: 这是一份初中数学人教版八年级上册15.2.1 分式的乘除教学演示ppt课件,共11页。PPT课件主要包含了考考你,知识链接,分式的乘除法法则,化为最简分数,解原式,分式的乘法法则,公因式,课堂练习,因式分解,x+3x-3等内容,欢迎下载使用。
数学八年级上册14.2.1 平方差公式复习课件ppt: 这是一份数学八年级上册14.2.1 平方差公式复习课件ppt,共16页。PPT课件主要包含了温故知新,自主学习,公式法,试一试,合作探究,巩固训练,变式训练分解因式,变式训练,谈谈你的感受,比一比等内容,欢迎下载使用。
初中数学人教版八年级上册14.1.2 幂的乘方备课课件ppt: 这是一份初中数学人教版八年级上册14.1.2 幂的乘方备课课件ppt,共24页。PPT课件主要包含了回顾旧知,探究活动,幂的乘方性质,归纳总结,文字语言,牛刀小试,计算3,巩固练习,大家来找茬,对接中考等内容,欢迎下载使用。












