


人教版七年级下册数学期中复习第五到七章复习课件
展开
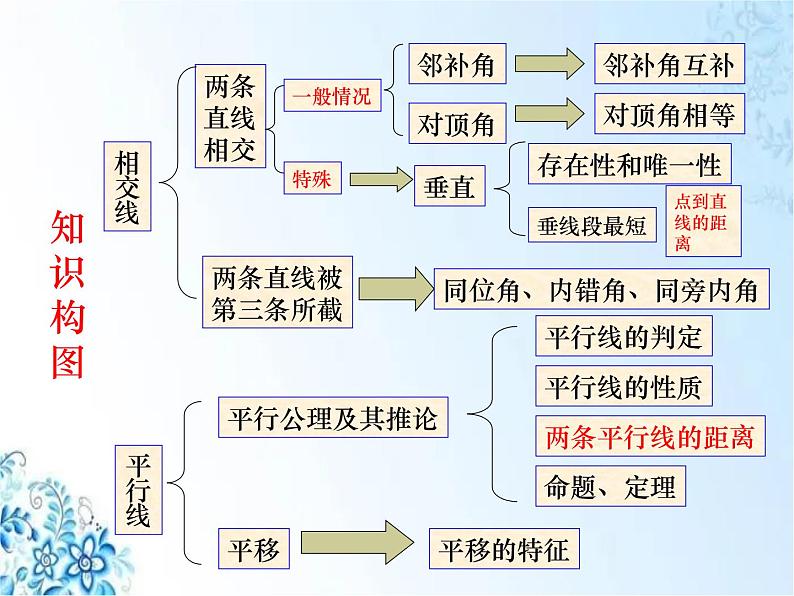
这是一份人教版七年级下册数学期中复习第五到七章复习课件,共60页。PPT课件主要包含了知识构图,三线八角,填空题,平方根的性质,你知道吗,不要搞错了,掌握规律,有理数,无理数,操作探索等内容,欢迎下载使用。
同位角、内错角、同旁内角
2. 对顶角: (1)两条直线相交所构成的四个角中,
有公共顶点但没有公共边的两个角是对顶角。如图(2).
(2)一个角的两边分别是另一个角的两边的反向延长线,这两个角是对顶角。
3. 邻补角的性质: 同角的补角相等。
4. 对顶角性质:对顶角相等。
两个特征:(1) 具有公共顶点;(2) 角的两边互为反向延长线。
n条直线相交于一点,就有n(n-1)对对顶角。
1.互为邻补角:两条直线相交所构成的四个角中,有公共顶点且有一条公共边的两个角是邻补角.如图(1)
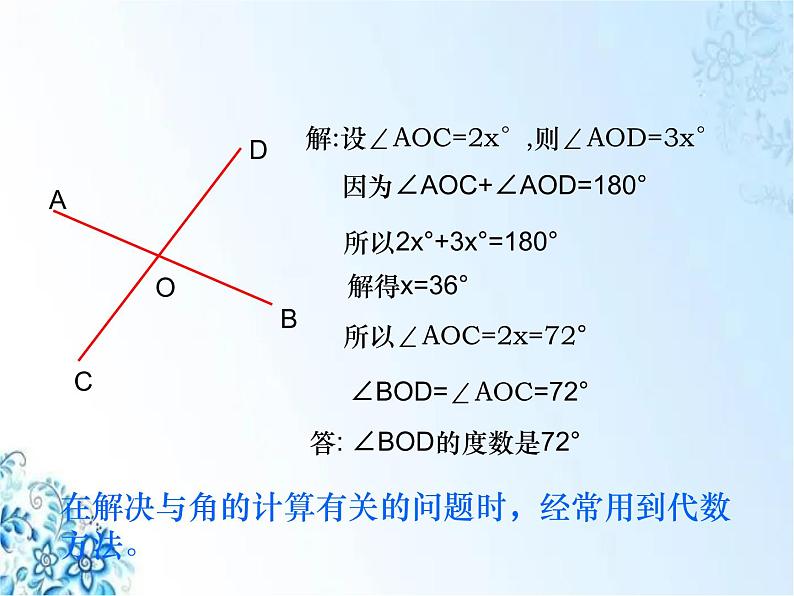
在解决与角的计算有关的问题时,经常用到代数方法。
解:设∠AOC=2x°,则∠AOD=3x°
所以2x°+3x°=180°
因为∠AOC+∠AOD=180°
所以∠AOC=2x=72°
∠BOD=∠AOC=72°
答: ∠BOD的度数是72°
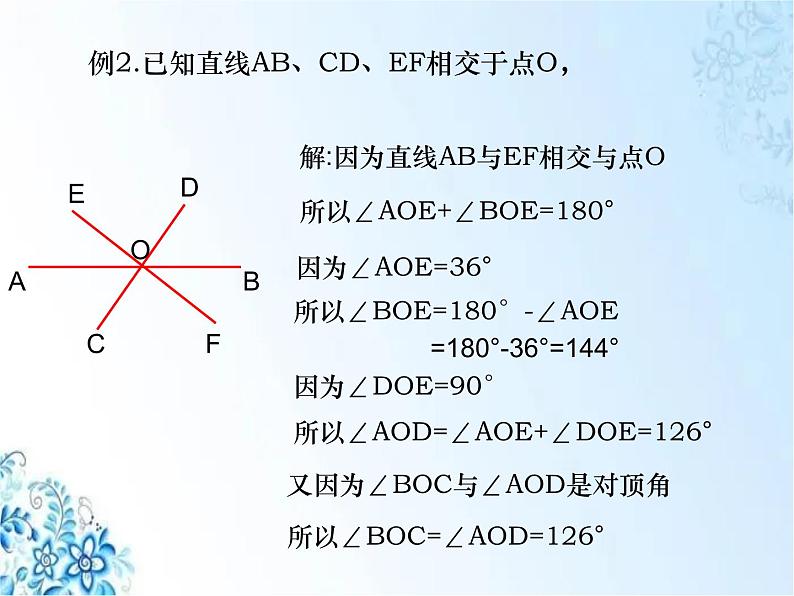
例2.已知直线AB、CD、EF相交于点O,
解:因为直线AB与EF相交与点O
所以∠AOE+∠BOE=180°
所以∠BOE=180°-∠AOE
=180°-36°=144°
所以∠AOD=∠AOE+∠DOE=126°
又因为∠BOC与∠AOD是对顶角
所以∠BOC=∠AOD=126°
1.垂线的定义: 两条直线相交,所构成的四个角中,有一个角是90°时,就说这两条直线互相垂直。其中一条直线叫做另一条直线的垂线。它们的交点叫垂足。
2. 垂线的性质: (1)过一点有且只有一条直线与已知直线垂直。(2): 直线外一点与直线上各点连结的所有线段中,垂线段最短。简称:垂线段最短。
3.点到直线的距离: 从直线外一点到这条直线的垂线段的长度,叫做点到直线的距离。
4.如遇到线段与线段,线段与射线,射线与射线,线段或射线与直线垂直时,特指它们所在的直线互相垂直。
5.垂线是直线,垂线段特指一条线段是图形,点到直线距离是指垂线段的长度,是指一个数量,是有单位的。
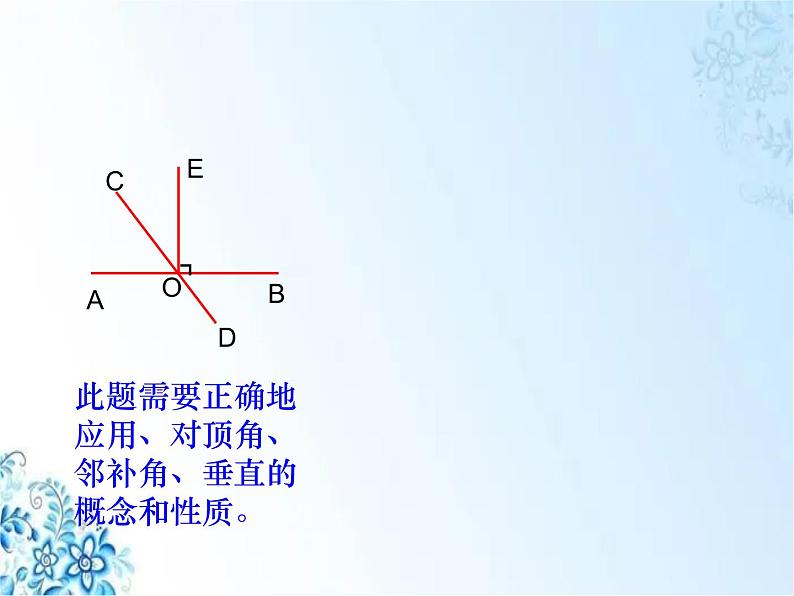
此题需要正确地
应用、对顶角、
邻补角、垂直的
概念和性质。
由垂直先找到90°的角,再根据角之间的关系求解。
例3:如图,要把水渠中的水引到水池C中,在渠岸的什么地方开沟,水沟的长度才能最短?请画出图来,并说明理由。
例4:你能量出C到AB的距离,B到AC的距离,A到BC的距离吗?
思考:三角形的三条垂线有什么特点?
三角形的三条垂线都交于一点;
锐角三角形的三条垂线交点在三角形的内部;
直角三角形的三条垂线交点在直角顶点;
钝角三角形的三条垂线交点在三角形的外部;
例5:你能画出ABC三点到对边的垂线吗?
平行线的概念:在同一平面内,不相交的两条直线叫做平行线。
2. 两直线的位置关系: 在同一平面内,两直线的位置关系只有两种:(1)相交; (2)平行。
3. 平行线的基本性质:
(1) 平行公理(平行线的存在性和唯一性) 经过直线外一点,有且只有一条直线与已知直线平行。
(2) 推论(平行线的传递性) 如果两条直线都和第三条直线平行,那么这两条直线也互相平行。
4.同位角、内错角、同旁内角的概念
同位角、内错角、同旁内角,指的是一条直线分别与两条直线相交构成的八个角中,不共顶点的角之间的特殊位置关系。它们与对顶角、邻补角一样,总是成对存在着的。
1、同位角的位置特征是:
2、内错角的位置特征是:
3、同旁内角的位置特征是:
(2)在被截两直线的同方向。
(2)在被截两直线之间。
(1)定义法;在同一平面内不相交的两条直线是平行线。
(2)传递法;两条直线都和第三条直线平行,这两条直线也平行。
(4)三种角判定(3种方法):
在这六种方法中,定义一般不常用。
同位角相等,两直线平行。
内错角相等,两直线平行。
同旁内角互补,两直线平行。
(3)因为a⊥c, a⊥b;所以b//c
判定两直线平行的方法有三种:
∠1和∠2不是同位角,
如图中的∠1和∠2是同位角吗? 为什么?
∵∠1和∠2无一边共线。
∵∠1和∠2有一边共线、同向
答:∠ BAC,∠BAE , ∠2
∠1与哪个角是同旁内角?
∠2与哪个角是内错角?
例1. ∠1与哪个角是内错角?
夹在两平行线间的垂线段的长度,叫做两平行线间的距离。
平
行
线
的
性
质
证明:由:∠1+∠2=180°(已知)
(同旁内角互补,两直线平行)
∠1=∠3(对顶角相等)
∠2=∠4(对顶角相等)
所以∠3+∠4=180°
例1. 如图 已知:∠1+∠2=180°,求证:AB∥CD。
证明: ∵由AC∥DE (已知)
∴ ∠ACD= ∠2
(两直线平行,内错角相等)
∵ ∠1=∠2(已知)
∴ ∠1=∠ACD (等量代换)
(内错角相等,两直线平行)
例2. 如图,已知:AC∥DE,∠1=∠2,试证明AB∥CD。
∵ EF⊥AB,CD⊥AB (已知)
(垂直于同一条直线的两条直线互相平行)
∴ ∠EFB= ∠DCB
(两直线平行,同位角相等)
∵ ∠EFB=∠GDC (已知)
∴ ∠DCB=∠GDC (等量代换)
(内错角相等,两直线平行)
∴ ∠AGD=∠ACB
例3.已知 EF⊥AB,CD⊥AB,∠EFB=∠GDC,求证:∠AGD=∠ACB。
如图,两平面镜а、β的夹角为θ,入射光线AO平行于β入射到а上,经两次反射后的反射光线O'B平行于а,且∠1=∠2,∠3=∠4,则角θ=_____度
例4. 两块平面镜的夹角应为多少度?
分析:由题意有OA//β,O'B∥a
且∠1=∠2,∠3=∠4,
由OA//β, ∠1=∠θ
O‘B∥a,∠4=∠θ,∠2=∠5
所以∠3=∠4 =∠5=∠θ
因为∠3+∠4+∠5 =180°
1. 命题的概念: 判断一件事情的句子,叫做命题。命题必须是一个完整的句子; 这个句子必须对某件事情做出肯定或者否定的判断。两者缺一不可。
2. 命题的组成: 每个命题是由题设、结论两部分组成。题设是已知事项;结论是由已知事项推出的事项。命题常写成“如果……,那么……”的形式。或 “若……,则……”等形式。真命题和假命题: 命题是一个判断,这个判断可能是正确的,也可以是错误的。由此可以把命题分成真命题和假命题。真命题就是: 如果题设成立,那么结论一定成立的命题。假命题就是: 如果题设成立时,不能保证结论总是成立的命题。
画线段AB=2cm直角都相等;两条直线相交,有几个交点?如果两个角不相等,那么这两个角不是对顶角。相等的角都是直角;
分析: 因为(1)、(3)不是对某一件事作出判断的句子,所以(1)、(3)不是命题。 解. (1)、(3)不是命题; (2)、(4)、(5)是命题; (2)、(4)都是真命,(5)是假命题。
例1. 判断下列语句,是不是命题,如果是命题,是真命题,还是假命题?
分析: 不妨选择(1)与(2)作条件,由平行性质 “两直线平行,同旁内角互补”可得∠A=∠C,故满足要求。由(1)与(3)也能得出(2)成立,由(2)与(3)也能得出(1)成立。
解: 如果在四边形ABCD中,AB//DC、AD//BC,那么∠A=∠C。
例2. 如图给出下列论断: (1)AB//CD (2)AD//BC (3)∠A=∠C以上,其中两个作为题设,另一个作为结论,用 “如果……,那么……”的形式,写出一个你认为正确的命题。
1. 平移变换的定义: 把一个图形整体沿某一方向移动,会得到 一个新图形,这样的图形运动,叫做平移变换,简称平移。平移的特征: (1)平移不改变图形的形状和大小。 (2)新图形中的每一点,都是由原图形中的某一点移动后得到 的,这两个点是对应点,对应点连结而成的线段平行且相等。决定平移的因素是平移的方向和距离。经过平移,图形上的每一点都沿同一方向移动相同的距离。经过平移,对应角相等;对应线段平行且相等; 对应点所连的线段平行且相等。
站在运动着的电梯上的人左右推动的推拉窗扇小李荡秋千运动躺在火车上睡觉的旅客
分析: A、B、D属平移,在一个位置取两点连成一条线,在另一个位置再观察这条线段,发现是平行的,而C同样取两点连成一条线段,运动到另一位置时,可能已不平行
例1. 在以下生活现象中,不是平移现象的是
例2. 如图所示,△ABC平移到△A′B′C′的位置,则点A的对应点是____,点B的对应点是____,点C的对应点是____。线段AB的对应线段是___________,线段BC的对应线段是______,线段AC的对应线段是_______。∠BAC的对应角是________,∠ABC的对应角是_________,∠ACB的对应角是_________。△ABC的平移方向是________________________________________,平移距离是_____________________________________________。
(或BB′,或CC′)的方向
(或线段BB′的长或线段CC′的长
1、邻补角、对顶角的概念和性质
2、垂线画法、垂线段的性质
3、平行线的判定和性质
4、命题的题设与结论以及命题的真假
5、平移的概念和平移的性质
人教版-七年级(下)数学期中复习
1.算术平方根的定义:
特殊:0的算术平方根是0。
如果一个数X的平方等于a,即X2=a,那么这个数X叫做a的平方根(二次方根)
求一个数a的平方根的运算叫做开平方,求一个数a的立方根的运算叫做开立方。
1.一个正数有两个平方根,它们互为相反数。 2.负数没有平方根。 3.0的平方根是0.
4.立方根的定义: 一般地,如果一个数的立方等于a,那么这个数就叫做a的立方根,也叫做a的三次方根.记作 .
平方根、立方根概念及性质
你知道算术平方根、平方根、立方根联系和区别吗?
求一个数的平方根的运算叫开平方
求一个数的立方根的运算叫开立方
-4,-3,-2,-1,0,1,2,3
注意平方根和立方根的移位法则
有限小数及无限循环小数
3.有一定的规律,但不循环的无限小数
里面的数的符号化简绝对值要看它
如图是两个边长1的正方形
拼成的长方形, 其面积是2.
现剪下两个角重新拼成一个
新正方形的边长是_____
下图数轴中, 正方形的对角线长
以原点为圆心, 对角线长为
与原点的距离是____,
该点表示的数是____.
实数与数轴上的点是一一对应关系.
在实数范围内,相反数、倒数、绝对值的意义和有理数范围内的相反数、倒数、绝对值的意义完全一样。
实数的大小比较方法多种,要具体观察实数的特点,灵活选择最好的比较方法
把下列各数分别填入相应的集合内:
(相邻两个3之间的7的个数逐次加1)
b a
第七章 平面直角坐标系
坐标(有序数对),(x, y)
在平面内有公共原点而且互相垂直的两条数轴,构成了平面直角坐标系.
规定:横坐标在前, 纵坐标在后
由坐标找点的方法:先找到表示横坐标与纵坐标的点,然后过这两点分别作x轴与y轴的垂线,垂线的交点就是该坐标对应的点。
若点P(x,y)在第一象限,则 x> 0,y> 0
若点P(x,y)在第二象限,则 x< 0,y> 0
若点P(x,y)在第三象限,则 x< 0,y< 0
若点P(x,y)在第四象限,则 x > 0,y< 0
三:各象限点坐标的符号
1.点P的坐标是(2,-3),则点P在第 象限.
3. 若点P(x,y)的坐标满足 xy﹤0,且在x轴上方,则点P在第 象限.
注:判断点的位置关键抓住象限内点的 坐标的符号特征.
4.若点A的坐标为(a2+1, -2–b2),则点A在第____象限.
A(3,0)在第几象限?
注:坐标轴上的点不属于任何象限。
四:坐标轴上点的坐标符号
1.点P(m+2,m-1)在x轴上,则点P的坐标是 .
2.点P(m+2,m-1)在y轴上,则点P的坐标是 .
3. 点P(x,y)满足 xy=0, 则点P在 .
x 轴上 或 y 轴上
4.若 ,则点p(x,y)位于 __
y轴(除(0,0))上
注意: 1. x轴上的点的纵坐标为0,表示为(x,0), 2. y轴上的点的横坐标为0, 表示为(0,y)。
原点(0,0)既在x轴上,又在y轴上。
(2). 若AB∥ y轴,
则A( m, y1 ), B( m, y2 )
(1). 若AB∥ x 轴,
则A( x1, n ), B( x2, n )
五:与坐标轴平行的两点连线
1. 已知点A(m,-2),点B(3,m-1),且直线AB∥x轴,则m的值为 。
2. 已知点A(m,-2),点B(3,m-1),且直线AB∥y轴,则m的值为 。
已知点A(10,5),B(50,5),则直线AB的位置特点是( )A.与x轴平行 B.与y轴平行C.与x轴相交,但不垂直 D.与y轴相交,但不垂直
(1). 若点P在第一、三象限角的平分线上,则P( m, m ).
(2). 若点P在第二、四象限角的平分线上则P( m, -m ).
六:象限角平分线上的点
3.已知点M(a+1,3a-5)在两坐标轴夹角的平分线上,试求M的坐标。
2.已知点A(2a+1,2+a)在第二象限的平分线上,试求A的坐标。
1.已知点A(2,y ),点B(x ,5 ),点A、B在一、三象限的角平分线上, 则x =____,y =____;
(1)点(a, b )关于X轴的对称点是( )
(2)点(a, b )关于Y 轴的对称点是( )
(3)点(a, b )关于原点的对称点是( )
七:关于坐标轴、原点的对称点
1.已知A、B关于x轴对称,A点的坐标为(3,2),则B的坐标为 。
2.若点A(m,-2),B(1,n)关于y轴对称,m= ,n= .
3.已知点A(3a-1,1+a)在第一象限的平分线上,试求A关于原点的对称点的坐标。
相关课件
这是一份人教版数学七年级下册期中复习课件,共16页。PPT课件主要包含了数量关系,位置关系,针对训练,3-2,个单位,-3-1等内容,欢迎下载使用。
这是一份数学七年级下册第五章 相交线与平行线综合与测试复习课件ppt,共48页。PPT课件主要包含了知识梳理,对顶角,邻补角,内错角,同旁内角,同位角,平行公理,知识结构图,应用提升,一题多解等内容,欢迎下载使用。
这是一份数学七年级下册第五章 相交线与平行线综合与测试复习课件ppt,共41页。PPT课件主要包含了相交线,知识梳理,平行线,平行公理,两条直线相交,邻补角,对顶角,角的计算依据,同位角,内错角等内容,欢迎下载使用。









