青岛版八年级上册第4章 数据分析综合与测试同步训练题

这是一份青岛版八年级上册第4章 数据分析综合与测试同步训练题，共9页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
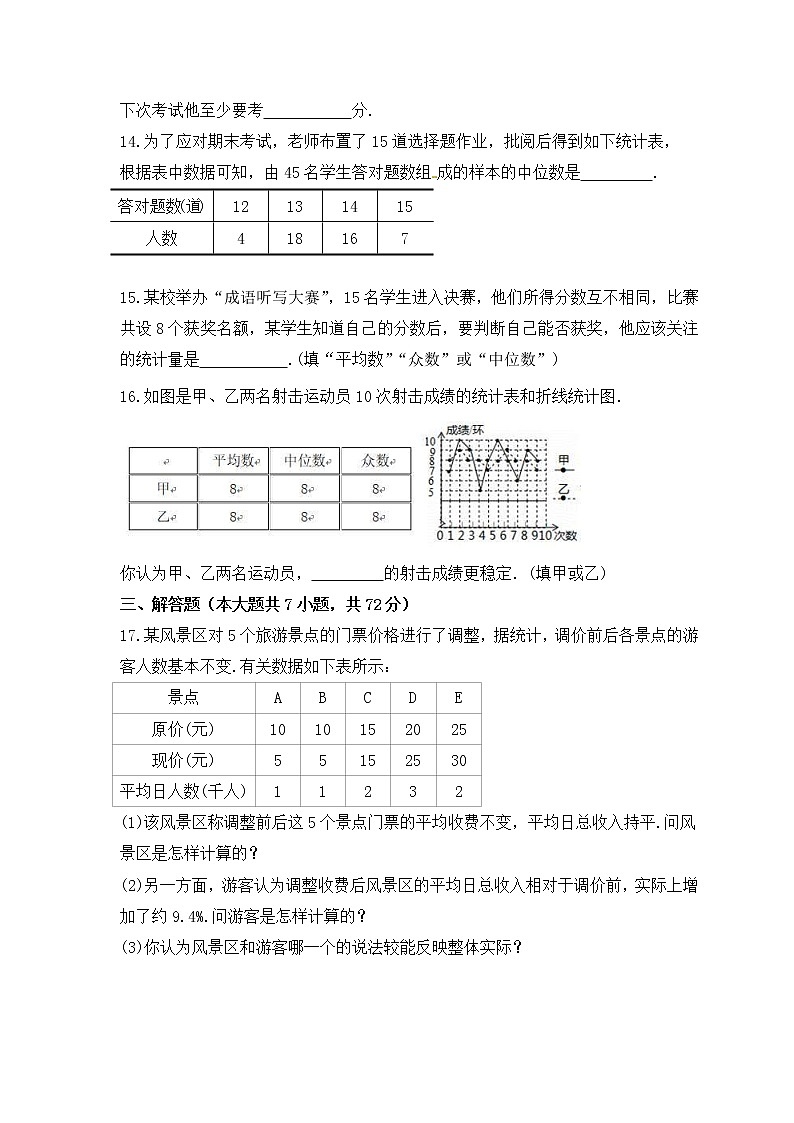
2022-2023年青岛版数学八年级上册第4章《数据分析》单元检测卷一              、选择题（本大题共10小题，每小题3分，共30分）1.一组数据7，8，10，12，13的平均数是（     ）A．7             B．9               C．10                 D．122.已知x1，x2，x3，……，x10的平均数是5，x11，x12，x13，……，x20的平均数是3，则x1，x2，x3，……，x20的平均数是(  )A.5       B.4        C.3       D.83.某区“引进人才”招聘考试分笔试和面试.其中笔试按60%、面试按40%计算加权平均数作为总成绩.吴老师笔试成绩为90分.面试成绩为85分，那么吴老师的总成绩为(　　)分.A.85        B.86         C.87            D.884.学校团委组织“阳光助残”捐款活动，九年一班学生捐款情况如下表：捐款金额（元）5102050人数（人）10131215则学生捐款金额的中位数是（　 　）A.13人                      B.12人                      C.10元                     D.20元5.已知一组数据3、4、4、5、6、7、4、7，那么这组数据的(    )A.中位数是5.5，众数是4B.中位数是5，平均数是5 C.中位数是5，众数是4D.中位数是4.5，平均数是56.某次数学趣味竞赛共有10道题目，每道题答对得10分，答错或不答得0分.全班40名同学的成绩的中位数和众数分别是（　　）A.75，70    B.70，70   C.80，80   D.75，80  7.制鞋厂准备生产一批男皮鞋，经抽样(120名中年男子)，得知所需鞋号和人数如下：并求出鞋号的中位数是24 cm，众数是25 cm，平均数约是24 cm，下列说法正确的是(　　)A.因为所需鞋号为27 cm的人数太少，所以鞋号为27 cm的鞋可以不生产B.因为平均数约是24 cm，所以这批男皮鞋可以一律按24 cm的鞋生产C.因为中位数是24 cm，所以24 cm的鞋的生产量应占首位D.因为众数是25 cm，所以25 cm的鞋的生产量应占首位8.在今年的八年级期末考试中，我校(1)(2)(3)(4)班的平均分相同，方差分别为S12=20.8，S22=15.3，S32=17，S42=9.6，四个班期末成绩最稳定的是(　　)A.(1)班         B.(2)班         C.(3)班         D.(4)班9.在样本方差的计算公式s2=[(x1﹣20)2+(x2﹣20)2+…+(x10﹣20)2]中，数字10与20分别表示样本的(　　)A.容量，方差                  B.平均数，容量      C.容量，平均数                D.标准差，平均数10.在“朗读者”节目的影响下，某中学开展了“好书伴我成长”的读书活动，为了解3月份八年级300名学生读书情况，随机调查了七年级50个学生读书的册数.统计数据如下表所示：册数01234人数41216171关于这组数据，下列说法正确的是（　　）A.众数是 17      B.平均数是 2      C.中位数是 2      D.方差是 2二              、填空题（本大题共6小题，每小题3分，共18分）11.若数据1、﹣2、3、x的平均数为2，则x=        ．12.如果x1与x2的平均数是4，那么x1＋1与x2＋5的平均数是      .13.小刚在最近的一次数学测试中考了93分，从而使本学期之前所有的数学测试平均分由73分提高到78分，他要想在下次考试中把本学期平均分提高到80分以上，下次考试他至少要考        分.14.为了应对期末考试，老师布置了15道选择题作业，批阅后得到如下统计表，根据表中数据可知，由45名学生答对题数组成的样本的中位数是     .答对题数(道)12131415人数418167 15.某校举办“成语听写大赛”，15名学生进入决赛，他们所得分数互不相同，比赛共设8个获奖名额，某学生知道自己的分数后，要判断自己能否获奖，他应该关注的统计量是           .(填“平均数”“众数”或“中位数”)16.如图是甲、乙两名射击运动员10次射击成绩的统计表和折线统计图． 你认为甲、乙两名运动员，　   　的射击成绩更稳定．(填甲或乙)三              、解答题（本大题共7小题，共72分）17.某风景区对5个旅游景点的门票价格进行了调整，据统计，调价前后各景点的游客人数基本不变.有关数据如下表所示：景点ABCDE原价(元)1010152025现价(元)55152530平均日人数(千人)11232(1)该风景区称调整前后这5个景点门票的平均收费不变，平均日总收入持平.问风景区是怎样计算的？(2)另一方面，游客认为调整收费后风景区的平均日总收入相对于调价前，实际上增加了约9.4%.问游客是怎样计算的？(3)你认为风景区和游客哪一个的说法较能反映整体实际？  18.某校为了招聘一名优秀教师，对入选的三名候选人进行教学技能与专业知识两种考核，现将甲、乙、丙三人的考核成绩统计如下：(1)如果校方认为教师的教学技能水平与专业知识水平同等重要，则候选人____将被录取.(2)如果校方认为教师的教学技能水平比专业知识水平重要，因此分别赋予它们6和4的权.计算他们赋权后各自的平均成绩，并说明谁将被录取.  19.下图是连续十周测试甲、乙两名运动员体能训练情况的折线统计图。教练组规定：体能测试成绩70分以上(包括70分)为合格。⑴请根据上图中所提供的信息填写下表：⑵请从下面两个不同的角度对运动员体能测试结果进行判断：①依据平均数与成绩合格的次数比较甲和乙，   的体能测试成绩较好；②依据平均数与中位数比较甲和乙，    的体能测试成绩较好。⑶依据折线统计图和成绩合格的次数，分析哪位运动员体能训练的效果较好。 20.车间有20名工人，某一天他们生产的零件个数统计如下表．车间20名工人某一天生产的零件个数统计表(1)求这一天20名工人生产零件的平均个数．(2)为了提高大多数工人的积极性，管理者准备实行“每天定额生产，超产有奖”的措施．如果你是管理者，从平均数、中位数、众数的角度进行分析，你将如何确定这个“定额”？   21.某校为了解七、八年级学生一分钟跳绳情况，从这两个年级随机抽取50名学生进行测试，并对测试成绩(一分钟跳绳次数)进行整理、描述和分析，下面给出了部分信息：七年级学生一分钟跳绳成绩(数据分7组：60≤x＜80，80≤x＜100，…，180≤x＜200)在100≤x＜120这一组的是：根据以上信息，回答下列问题：(1)表中a=　   　；(2)在这次测试中，七年级甲同学的成绩122次，八年级乙同学的成绩125次，他们的测试成绩，在各自年级所抽取的50名同学中，排名更靠前的是　   　(填“甲”或“乙”)，理由是　   　．(3)该校七年级共有500名学生，估计一分钟跳绳不低于116次的有多少人？ 22.王华、张伟两位同学分别将自己10次数学自我检测的成绩绘制成如下统计图：（1）根据上图中提供的数据列出如下统计表： 平均成绩（分）中位数（分）众数（分）方差（S2）王华    80    b   80    d张伟     a    85    c   260则a=       ，b=       ，c=       ，d=      ，（2）将90分以上（含90分）的成绩视为优秀，则优秀率高的是        .（3）现在要从这两个同学选一位去参加数学竞赛，你可以根据以上的数据给老师哪些建议？ 23.某校为了了解初中学生每天的睡眠时间(单位为小时)，随机调查了该校的部分初中学生，根据调查结果，绘制出如下统计图．请根据相关信息，解答下列问题：(1)本次接受调查的初中学生人数为___________人，扇形统计图中的m=________，条形统计图中的n=_____；(2)所调查的初中学生每天睡眠时间的众数是____________，方差是___________；(3)该校共有1600名初中学生，根据样本数据，估计该校初中学生每天睡眠时间不足8小时的人数．
参考答案1.C2.B3.D4.D．5.D6.A7.D.8.D.9.C.10.C.11.答案为：6．12.答案为：7.13.答案为：8814.答案为：14.15.答案为：中位数；16.答案为：乙. 17.解：(1)风景区是这样计算的：调整前的平均价格： =16(元)调整后的平均价格： =16(元)∵调整前后的平均价格不变，平均日人数不变∴平均日总收入持平；(2)游客是这样计算的：原平均日总收入：10×1+10×1+15×2+20×3+25×2=160(千元)现平均日总收入：5×1+5×1+15×2+25×3+30×2=175(千元)∴平均日总收入增加了：9.4%；(3)根据加权平均数的定义可知，游客的算法是正确的，故游客的说法较能反映整体实际. 18.解：(1)甲的平均成绩是(85＋92)÷2=88.5(分)，乙的平均成绩是(91＋85)÷2=88(分)，丙的平均成绩是(80＋90)÷2=85(分)，∵甲的平均成绩最高，∴候选人甲将被录取.(2)甲的平均成绩是(85×6＋92×4)÷(6＋4)=87.8(分)，乙的平均成绩是(91×6＋85×4)÷(6＋4)=88.6(分)，丙的平均成绩是(80×6＋90×4)÷(6＋4)=84(分)，∵候选人乙的平均成绩最高，∴候选人乙将被录取.19.解：⑴如下表： 平均数中位数体能测试成绩合格次数甲60652乙6057.54⑵①乙；②甲⑶从折线图上看，两名运动员体能测试成绩都呈上升趋势，但是，乙的增长速度比甲快，并且后一阶段乙的成绩合格次数比甲多，所以乙训练的效果较好。20.解：(1)=×(9×1+10×1+11×6+12×4+13×2+15×2+16×2+19×1+20×1)=13(个)；答：这一天20名工人生产零件的平均个数为13个；(2)中位数为=12(个)，众数为11个，当定额为13个时，有8人达标，6人获奖，不利于提高工人的积极性；当定额为12个时，有12人达标，6人获奖，不利于提高大多数工人的积极性；当定额为11个时，有18人达标，12人获奖，有利于提高大多数工人的积极性；∴定额为11个时，有利于提高大多数工人的积极性．   21.解：(1)∵七年级50名学生成绩的中位数是第25、26个数据的平均数，而第25、26个数据分别是117、119，∴中位数a==118，故答案为：118；(2)∴在各自年级所抽取的50名同学中，排名更靠前的是甲，理由是甲的成绩122超过中位数118，乙的成绩125低于其中位数126，故答案为：甲，甲的成绩122超过中位数118，乙的成绩125低于其中位数126．(3)估计一分钟跳绳不低于116次的有500×=270(人)．22.解：（1）王华10次成绩分别为：80,70,90,80,70，90,70,80,90,80；按大小顺序排列为：70,70,70,80,80,80,80,90,90,90则中位数b=80方差；张伟的平均成绩90出现了3次，出现的次数最多，则众数c=90；故答案为80,80,90,60（2）王华的优秀率为：张伟的优秀率为：则张伟的优秀率高.23.解：(1)由图表中的数据可得：8÷20%=40人，10÷40×100%=25%，即m=25，40×37.5%=15人，即n=15，故答案为：40；25；15；(2)由条形统计图可得：∵睡眠时间诶7h的人数为15人，最多，∴众数是：7，平均数是：7，方差是1.15，(3)1080人，∴该校初中学生每天睡眠时间不足8小时的人数为1080人．