专题01 集合 （知识串讲+热考题型+专题训练）-2022-2023学年高一数学上学期期中期末考点大串讲（苏教版2019必修第一册）

这是一份专题01 集合 （知识串讲+热考题型+专题训练）-2022-2023学年高一数学上学期期中期末考点大串讲（苏教版2019必修第一册），文件包含专题01集合知识串讲+热考题型+专题训练-2022-2023学年高一数学上学期期中期末考点大串讲苏教版2019必修第一册解析版docx、专题01集合知识串讲+热考题型+专题训练-2022-2023学年高一数学上学期期中期末考点大串讲苏教版2019必修第一册原卷版docx等2份试卷配套教学资源，其中试卷共33页， 欢迎下载使用。

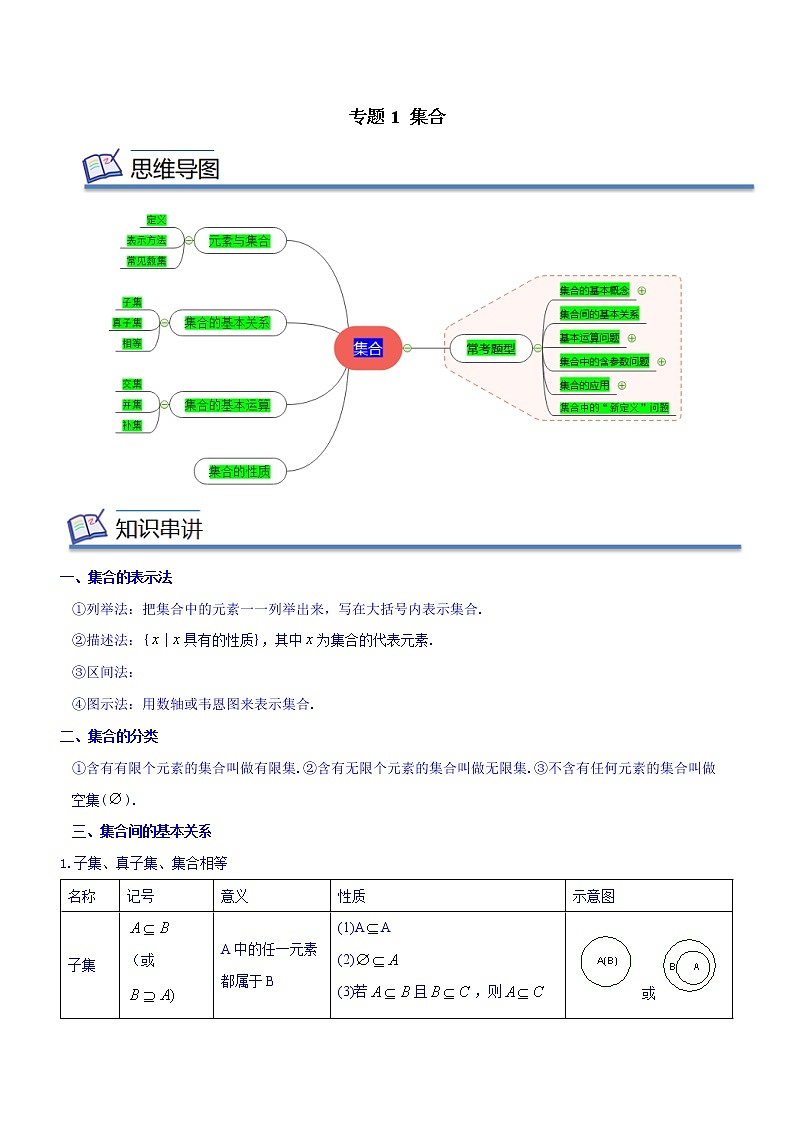
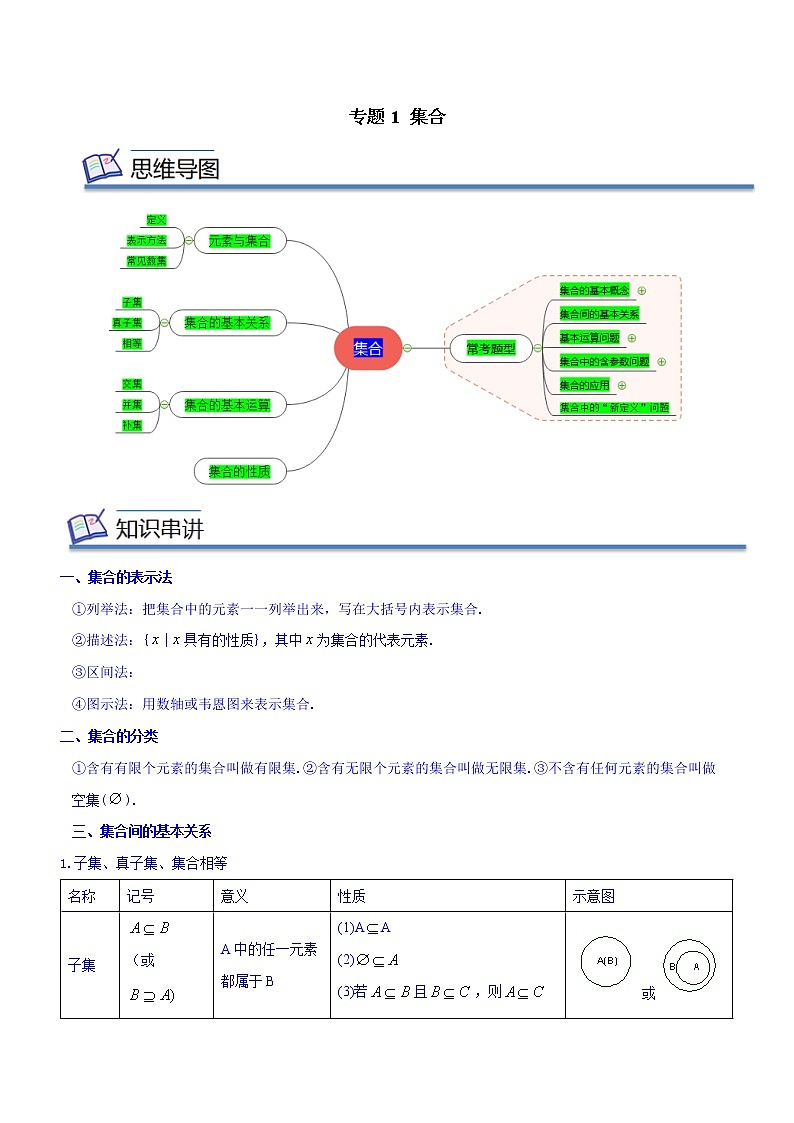
专题1 集合


一、集合的表示法
①列举法：把集合中的元素一一列举出来，写在大括号内表示集合.
②描述法：{|具有的性质}，其中为集合的代表元素.
③区间法：
④图示法：用数轴或韦恩图来表示集合.
二、集合的分类
①含有有限个元素的集合叫做有限集.②含有无限个元素的集合叫做无限集.③不含有任何元素的集合叫做空集().
三、集合间的基本关系
1.子集、真子集、集合相等
名称
记号
意义
性质
示意图
子集

（或
A中的任一元素都属于B
(1)AA
(2)
(3)若且，则
(4)若且，则
或
真子集
AB
（或BA）
，且B中至少有一元素不属于A
（1）（A为非空子集）
(2)若且，则

集合
相等

A中的任一元素都属于B，B中的任一元素都属于A
(1)AB
(2)BA

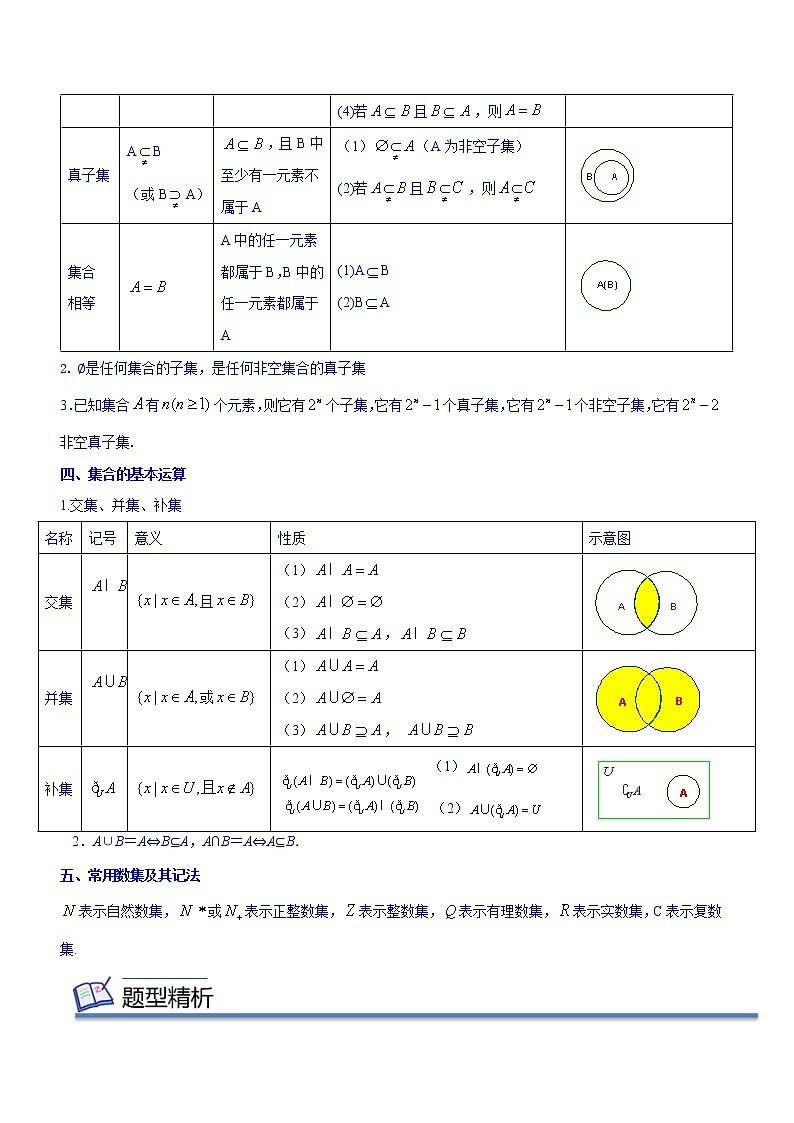
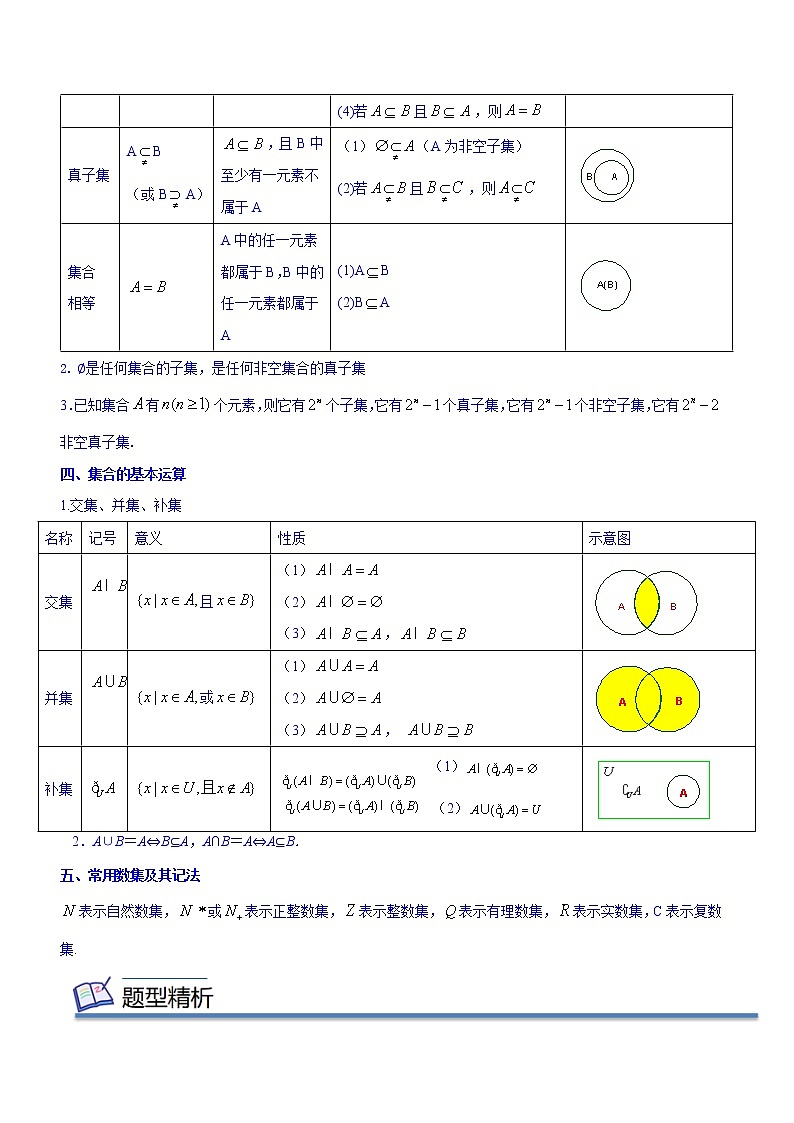
2. ∅是任何集合的子集，是任何非空集合的真子集
3．已知集合有个元素，则它有个子集，它有个真子集，它有个非空子集，它有非空真子集.
四、集合的基本运算
1.交集、并集、补集
名称
记号
意义
性质
示意图
交集

且
（1）
（2）
（3），

并集

或
（1）
（2）
（3），

补集


（1） （2）

2．A∪B＝A⇔B⊆A，A∩B＝A⇔A⊆B．
五、常用数集及其记法
表示自然数集，或表示正整数集，表示整数集，表示有理数集，表示实数集，C表示复数集.

题型一 集合的基本概念
【典例1】（2022·全国·高一课时练习）下列元素与集合的关系中，正确的是（    ）
A． B． C． D．
【答案】B
【分析】由分别表示的数集，对选项逐一判断即可.
【详解】不属于自然数，故A错误；
不属于正整数，故B正确；
是无理数，不属于有理数集，故C错误；
属于实数，故D错误.
故选:B.
【典例2】(2018课标II理2)已知集合，则中元素的个数为 （ ）
A．9 B．8 C．5 D．4
【答案】A

方法二：根据集合A的元素特征及圆的方程在坐标系中作出图形，如图，易知在圆x2＋y2＝3中有9个整点，即为集合A的元素个数，故选A.

【典例3】（2022·全国·高一课时练习）已知集合，，则集合B中元素的个数为______.
【答案】6
【分析】由已知，根据条件给的集合A，按照集合B给的定义列举即可完成求解.
【详解】因为，，，所以时，；时，或，时，或3或4.，所以集合B中元素的个数为6.
故答案为：6.
【规律方法】
与集合元素有关问题的思路：
（1）确定集合的元素是什么，即确定这个集合是数集还是点集．
（2）看这些元素满足什么限制条件．
（3）根据限制条件列式求参数的值或确定集合元素的个数，但要注意检验集合是否满足元素的互异性
题型二：集合间的基本关系
【典例4】（2022·河南·开封市东信学校模拟预测）集合的非空真子集的个数为（       ）
A．5 B．6 C．7 D．8
【答案】B
【解析】
【分析】
根据真子集的定义即可求解.
【详解】
由题意可知，集合A的非空真子集为，共6个.
故选：B.
【易错警示】空集是任何集合的子集，在涉及集合关系时，必须优先考虑空集的情况，否则会造成漏解．
【典例5】（2022·北京·101中学高一阶段练习）已知集合满足，则满足要求的的个数是______．
【答案】7
【分析】根据给定条件分析出集合M中一定有的元素及可能有的元素即可得解.
【详解】因为，于是得，且集合M中至少包含集合中的元一个素，
因此，集合的个数就是集合的非空子集个数，
而集合的非空子集个数为，
所以集合的个数为7.
故答案为：7.
【方法技巧】
(1)判断两集合之间的关系的方法：当两集合不含参数时，可直接利用数轴、图示法进行判断；当集合中含有参数时，需要对满足条件的参数进行分类讨论或采用列举法．
(2)要确定非空集合A的子集的个数，需先确定集合A中的元素的个数，再求解．不要忽略任何非空集合是它自身的子集．
题型三 基本运算问题
【典例6】（2022·全国·高考真题（文））设集合，则（       ）
A． B． C． D．
【答案】A
【解析】
因为，，所以．
故选：A.
【典例7】（2021·江苏·姜堰中学高一期中）若集合，，则（    ）
A． B． C． D．
【答案】D
【分析】根据集合的并集运算可得答案.
【详解】因为，，所以
故选：D
【典例8】（2021·江苏南京·高一期中）已知全集，集合，则（    ）
A． B． C． D．
【答案】B
【分析】根据补集的定义计算可得；
【详解】解：∵全集，集合，∴．
故选：B．
【典例9】（2022·全国·高考真题（理））设全集，集合，则（       ）
A． B． C． D．
【答案】D
【解析】
【分析】
解方程求出集合B,再由集合的运算即可得解.
【详解】
由题意，，所以,
所以.
故选：D.
【典例10】（2020·全国·高考真题（文））已知集合，，则A∩B中元素的个数为（       ）
A．2 B．3 C．4 D．5
【答案】B
【解析】
【分析】
采用列举法列举出中元素的即可.
【详解】
由题意，，故中元素的个数为3.
故选：B
【规律方法】
（1）认清元素的属性．解决集合问题时，认清集合中元素的属性(是点集、数集或其他情形)和化简集合是正确求解的两个先决条件．
（2）若集合中的元素是连续的实数，则用数轴（区间）表示，此时要注意端点是实心还是空心．
题型四 集合中的含参数问题
【典例11】【多选题】（2021·江苏·盐城市田家炳中学高一期中）设，．若，则实数的值可以为（    ）
A．1 B．2 C．0 D．
【答案】ACD
【分析】由得,分类讨论集合B的元素情况，即可求得答案.
【详解】由得：,
当时，,符合题意；
当时，，若，则；若，则；
由于B中至多有一个元素，故,
所以实数的值可以为，
故选：ACD
【典例12】【多选题】（2021·湖北孝感·高一期中）已知集合，，则为（    ）
A．2 B． C．5 D．
【答案】BC
【分析】结合元素与集合的关系，集合元素的互异性来求得的值.
【详解】依题意，
当时，或，
若，则，符合题意；
若，则，对于集合，不满足集合元素的互异性，所以不符合.
当时，或，
若，则，对于集合，不满足集合元素的互异性，所以不符合.
若，则，符合题意.
综上所述，的值为或.
故选：BC
【典例13】（2022·湖南·株洲二中高一开学考试）已知集合，若，则实数___________.
【答案】或3##3或-2
【分析】利用子集关系可知，或，求出再验证即得结果.
【详解】，
∴或，
解得或或，
将的值代入集合、验证，知不符合集合的互异性，
故或3.
故答案为：或3.
【典例14】（2017·江苏·高考真题）已知集合，，若则实数的值为________
【答案】1
【解析】
【详解】
由题意，显然，所以，此时，满足题意，故答案为1．
【总结提升】
（1）已知两个集合间的关系求参数时，关键是将条件转化为元素或区间端点间的关系，进而转化为参数所满足的关系，常用数轴、Venn图等来直观解决这类问题．
（2）空集是任何集合的子集，当题目条件中有B⊆A时，应分B＝∅和B≠∅两种情况讨论，确定参数所满足的条件时，一定要把端点值代入验证，否则易增解或漏解．
（3）在解决含参数的集合问题时，要注意检验集合中元素的互异性，否则很可能会因为不满足“互异性”而导致错误．
题型五 集合的应用
【典例15】（2021·江苏淮安·高一期中）某年级举行数学、物理、化学三项竞赛，共有名学生参赛，其中参加数学竞赛有人，参加物理竞赛有45人，参加化学竞赛有30人，同时参加物理、化学竞赛有人，同时参加数学、物理竞赛有人，同时参加数学、化学竞赛有10人，这个年级三个学科竞赛都参加的学生共有_______名．
【答案】10
【分析】将参加三种竞赛的人数情况画出韦恩图，根据题干数据分析，即得解.
【详解】
将参加三种竞赛的人数情况画出韦恩图，如图所示
不妨设这个年级三个学科竞赛都参加的学生共有人，
则只参加数学、化学竞赛的有人，只参加物理、化学竞赛的有人，
只参加数学、物理竞赛的有人，
只参加数学竞赛的有人
只参加物理竞赛的有人
只参加化学竞赛的有人
故参见竞赛的总人数
解得
故答案为：10
【典例16】（2021·江苏·徐州市第七中学高一期中）学校举办运动会时，高一（1）班共有28名同学参加比赛，有15人参加游泳比赛，有8人参加田径比赛，有14人参加球类比赛，同时参加游泳比赛和田径比赛的有3人，同时参加游泳比赛和球类比赛的有3人，没有人同时参加三项比赛，同时参加由径和球类比赛的有___________人?只参加游泳一项比赛的有___________人?
【答案】     3     9
【分析】结合韦恩图，利用集合的基本运算求解.
【详解】解：如图所示：

设A={游泳}，B={田径}，C={球类}，
由题意得：，
，
所以，
则，
，
所以，
所以参加由径和球类比赛的有3人，只参加游泳一项比赛的有9人，
故答案为：3，9
【总结提升】
涉及集合中元素的个数计算问题，借助于韦恩图具有形象直观的特点，可降低解题难度
题型六 集合中的“新定义”问题
【典例17】【多选题】（2020·江苏苏州·高一期中）已知A，B为再集合，定义，则下列命题中为真的有（    ）
A．若，则
B．若，则
C．若，则
D．若，则
【答案】BD
【分析】举例否定A;举例否定C;根据定义，利用几何相等的定义进行论证，可判定B正确；根据空集的定义，结合新定义，可以证明D正确.
【详解】当时，,故错误；
当时，,故错误；
由定义可知时，,故B正确；
当时，故D正确.
故选：BD.
【典例18】【多选题】（2022·山东青岛·高二期末）非空集合关于运算满足：对于任意的、，都有，则称集合关于运算为“回归集”．下列集合关于运算为“回归集”的是（       ）
A．为，为自然数的减法
B．为，为有理数的乘法
C．为，为实数的加法
D．已知全集，集合，为，为实数的乘法
【答案】BC
【解析】
【分析】
对每个选项逐一判断，结合实数的运算以及特殊值法判断可得出合适的选项.
【详解】
对于A选项，若，为自然数的减法，则，A不满足条件；
对于B选项，若，对任意的、，则，B满足条件；
对于C选项，若，对任意的、，则，C满足条件；
对于D选项，已知全集，集合，，取，，
则，D不满足条件.
故选：BC.
【方法技巧】
解决集合新定义问题的方法
(1)正确理解新定义：耐心阅读，分析含义，准确提取信息是解决这类问题的前提，剥去新定义、新法则、新运算的外表，利用所学的集合性质等知识将陌生的集合转化为我们熟悉的集合，是解决这类问题的突破口.
(2)合理利用集合性质：运用集合的性质(如元素的性质、集合的运算性质等)是破解新定义型集合问题的关键．在解题时要善于从题设条件给出的数式中发现可以使用集合性质的一些因素，并合理利用.
(3)对于选择题，可结合选项，通过验证、排除、对比、特值法等进行求解或排除错误选项，当不满足新定义的要求时，只需通过举反例来说明，以达到快速判断结果的目的.

一、选择题：
1．（2022·浙江·杭十四中高一期中）设全集，集合，则（    ）
A． B． C． D．
【答案】C
【分析】根据并集的定义直接求解即可.
【详解】因为，
所以，
故选：C
2．（2016·天津市红桥区教师发展中心高一期中）下列各式中关系符号运用正确的是（    ）
A． B．
C． D．
【答案】C
【分析】根据元素和集合的关系，集合与集合的关系，空集的性质判断即可.
【详解】根据元素和集合的关系是属于和不属于，所以选项A错误；
根据集合与集合的关系是包含或不包含，所以选项D错误；
根据空集是任何集合的子集，所以选项B错误，故选项C正确.
故选：C.
3．（2021·江苏省丹阳高级中学高一期中）已知集合，，则图中阴影部分表示的集合为（    ）


A． B． C． D．
【答案】A
【解析】由图可知，阴影部分为集合的交集.
【详解】图中阴影部分表示的集合为，
故选：A
4.（2022·全国·高考真题（理））设全集，集合M满足，则（       ）
A． B． C． D．
【答案】A
【解析】
【分析】
先写出集合,然后逐项验证即可
【详解】
由题知,对比选项知，正确,错误
故选:
5．（2022·全国·高一课时练习）已知集合，，则（    ）
A． B．或 C． D．
【答案】D
【分析】依题意可得或，分别求出的值，再代入检验是否满足集合元素的互异性，即可得解.
【详解】∵，∴或．
若，解得或．
当时，，不满足集合中元素的互异性，故舍去；
当时，集合，满足题意，故成立．
若，解得，由上述讨论可知，不满足题意，故舍去．
综上所述，．
故选：D．
6．（2021·江苏·东海县教育局教研室高一期中）已知集合A，B和全集U={1，2，3，4}，且A={1，2，3}，B={3，4}，则（    ）
A．{4} B． C．{3，4} D．{3}
【答案】A
【分析】求出，再求交集即可.
【详解】因为，，
所以.
故选：A.
7．（2022·广东·深圳实验学校高一期中）已知集合，，若满足，则的值为(    )
A．或5 B．或5 C． D．5
【答案】C
【分析】根据可知9∈A，则或由此可求出a的值，分类讨论即可确定符合题意的a的取值．
【详解】∵，∴9∈A，或，解得或或，
当时，，，此时，不符合题意；
当时，，集合不满足元素的互异性，不符合题意；
当时，，，此时，符合题意；
综上，
故选：C．
8．（2022·全国·高一专题练习）已知，，为非零实数，代数式的值所组成的集合是，则下列判断正确的是（       ）
A． B． C． D．
【答案】A
【解析】
【分析】
分别对，，的符号进行讨论，计算出集合的所有元素，再进行判断.
【详解】
根据题意，分4种情况讨论；
①、全部为负数时，则也为负数，则；
②、中有一个为负数时，则为负数，则；
③、中有两个为负数时，则为正数，则；
④、全部为正数时，则也正数，则；
则；分析选项可得符合．
故选：A.
二、多项选择题：
9．（2022·全国·高一专题练习）下列关系正确的是（        ）
A． B．
C． D．Ü
【答案】ABD
【解析】
【分析】
利用元素与集合之间的关系，集合与集合之间的关系判断即可.
【详解】
由空集的定义知：，A正确.
,B正确.
，C错误.
Ü,D正确.
故选：ABD.
10．（2022·江苏·高一）若Ü，则(       )
A． B． C． D．
【答案】ABC
【解析】
【分析】
根据题意可知集合B最少包含1，2两个元素，最多包含1，2，3或1，2，4三个元素.
【详解】
∵Ü，
∴B＝{1，2}或B＝{1，2，3}或B＝{1，2，4}.
故选：ABC.
11.（2022·全国·高三专题练习）下面说法中，正确的为（       ）
A． B．
C． D．
【答案】ACD
【解析】
【分析】
根据集合的定义，表示方法及集合相等的条件逐个分析判断
【详解】
解：方程中x的取值范围为R，所以，同理，所以A正确；
表示直线上点的集合，而，所以，所以B错误；
集合，都表示大于2的实数构成的集合，所以C正确；
由于集合的元素具有无序性，所以，所以D正确．
故选：ACD．
12．（2021·湖北·黄石市有色第一中学高一期中）对于集合A，B，定义，．设，，则中可能含有下列元素（    ）．
A．5 B．6 C．7 D．8
【答案】CD
【分析】根据所给定义求出，，即可求出，从而判断即可；
【详解】解：因为，，所以，
∴．
故选：CD
三、填空题：
13．（2021·江苏·南京市金陵中学河西分校高一期中）已知全集U＝，且＝{2}，则A＝______．
【答案】##{1,0}.
【分析】根据补集的定义，结合全集中的元素，即可求得结果.
【详解】因为全集U＝，且＝{2}，则.
故答案为：.
14．（2022·上海金山·二模）已知集合，若，则实数的值为__________.
【答案】0
【解析】
【分析】
解方程即得解.
【详解】
解：因为，所以（舍去）或，
所以.
故答案为：0
15．（2022·全国·高一专题练习）已知且，则由的值构成的集合是_______ .
【答案】
【解析】
【分析】
由集合的互异性列出不等式解得答案即可.
【详解】
，；或，解得.
故答案为：．
16．（2022·全国·高一专题练习）设集合，其中，且，若，则中的元素之和为_____.
【答案】0
【解析】
【分析】
根据元素与集合间的关系，列方程求解.
【详解】
因为，所以若，则集合不成立．所以．
若因为，所以，所以必有，所以．
因为，，所以或．
若，此时不成立，舍去．
若，则，成立．所以元素之和为．
故答案为：0.
四、解答题：
17.（2021·江苏·扬州大学附属中学高一期中）已知集合，，.
(1)求；
(2)求.
【答案】(1)
(2)
【解析】
【分析】
（1）利用并集的概念即可求解；
（2）利用交集及补集的运算即可求解.
(1)
，，

(2)
∵，，
∴，又
故．
18．（2022·广西桂林·高一期末）已知全集.
(1)求；
(2)求.
【答案】(1)
(2)
【解析】
【分析】
（1）根据交集计算可得.
（2）根据补集与并集的计算可得.
(1)
由己知，
所以
(2)
∵，
所以，
所以.
19.（2022·湖南·高一课时练习）已知集合，均为全集的子集，且，，求．
【答案】
【解析】
【分析】
求出集合的补集，然后由可知，进而由交集的定义得出结果．
【详解】
解：∵全集，，
∴
∵，
∴
∴.
20．（2020·广东·新会陈经纶中学高一期中）已知集合，，全集.求：
(1)；
(2).
【答案】(1)
(2)=
【解析】
【分析】
（1）先求得集合A，根据交集运算的概念，即可得答案.
（2）先求得集合A的补集，根据并集运算的概念，即可得答案.
(1)
由，解得，，
；
(2)
，
，
=
21．（2021·江苏·金湖中学高一期中）已知集合.
(1)求：
(2)若，求实数a的取值范围.
【答案】(1)，
(2)
【分析】（1）画数轴即可求出；求出集合在R上的补集再与取并集即可得到答案.
（2）由知，集合是集合的子集，并且集合明显不为 ，因此可得出，解不等式组即可得到答案.
(1)
由题意集合，集合
所以，
所以，
所以；
(2)
因为；由，解得；
所以实数a的取值范围是.
22．（2020·江苏·常州市北郊高级中学高一期中）已知集合或，集合

（1）若，求和;
（2）若记符号且，在图中把表示“集合”的部分用阴影涂黑，并求当时的;
（3）若，求实数a的取值范围.
【答案】（1），或；（2）阴影图形见解析，或；（3）或.
【解析】（1）当时，求得集合B，根据交集、并集的运算法则，即可求得答案；
（2）阴影图形见解析，当时，求得集合B，根据的定义，即可求得答案；
（3）由题意得，分别讨论和两种情况，根据集合的包含关系，即可求得a的范围.
【详解】（1）当时，，
所以，或；
（2）A-B的部分如图所示：，
当时，或；
（3）因为，所以，
当时，，解得，
当时，则或，
解得或，
综上：或.
【点睛】易错点为：根据集合包含关系求参数时，当，且集合B含有参数时，需要讨论集合B是否为空集，再进行求解，考查分析理解，计算求值的能力，属中档题.