



- 专题01 集合 (知识串讲+热考题型+专题训练)-2022-2023学年高一数学上学期期中期末考点大串讲(苏教版2019必修第一册) 试卷 4 次下载
- 专题02 常用逻辑用语 (知识串讲+热考题型+专题训练)-2022-2023学年高一数学上学期期中期末考点大串讲(苏教版2019必修第一册) 试卷 2 次下载
- 专题04 指数与对数 (知识串讲+热考题型+专题训练)-2022-2023学年高一数学上学期期中期末考点大串讲(苏教版2019必修第一册) 试卷 4 次下载
- 专题05 函数概念与性质(知识串讲+热考题型+专题训练)-2022-2023学年高一数学上学期期中期末考点大串讲(苏教版2019必修第一册) 试卷 4 次下载
- 期中模拟试卷1-2022-2023学年高一数学上学期期中期末考点大串讲(苏教版2019必修第一册) 试卷 2 次下载
专题03 不等式 (知识串讲+热考题型+专题训练)-2022-2023学年高一数学上学期期中期末考点大串讲(苏教版2019必修第一册)
展开专题03 不等式
(一)不等式的性质
1.比较大小的常用方法
(1)作差法
一般步骤:①作差;②变形;③定号;④结论.其中关键是变形,常采用配方、因式分解、有理化等方法把差式变成积式或者完全平方式.当两个式子都为正数时,有时也可以先平方再作差.
(2)作商法
一般步骤:①作商;②变形;③判断商与1的大小关系;④结论.
*(3)函数的单调性法
将要比较的两个数作为一个函数的两个函数值,根据函数的单调性得出大小关系.
2.判断不等式是否成立的方法
(1)判断不等式是否成立,需要逐一给出推理判断或反例说明.
(2)在判断一个关于不等式的命题的真假时,可结合不等式的性质,对数函数、指数函数的性质进行判断.
3.求代数式的取值范围
利用不等式性质求某些代数式的取值范围时.一般是利用整体思想,通过“一次性”不等关系的运算求得整体范围,是避免错误的有效途径.
4.不等式性质
(1)对称性:a>b⇔b<a.
(2)传递性:a>b,b>c⇒a>c.
(3)可加性:a>b⇒a+c>b+c.
(4)可乘性:a>b,c>0⇒ac>bc;a>b,c<0⇒ac<bc.
(5)加法法则:a>b,c>d⇒a+c>b+d.
(6)乘法法则:a>b>0,c>d>0⇒ac>bd.
(7)乘方法则:a>b>0⇒an>bn(n∈N,n≥2).
(8)开方法则:a>b>0⇒>(n∈N,n≥2).
(二)基本(均值)不等式
1.重要不等式
当a、b是任意实数时,有a2+b2≥2ab,当且仅当a=b时,等号成立.
2.基本不等式
当a>0,b>0时有,当且仅当a=b时,等号成立.
3.常用推论
(1)()
(2)(,);
(3)
(三)基本(均值)不等式应用
1.基本不等式与最值
已知x、y都是正数.
(1)若x+y=s(和为定值),则当x=y时,积xy取得最大值.
(2)若xy=p(积为定值),则当x=y时,和x+y取得最小值.
2. 利用基本不等式求解实际应用题的方法
(1)此类型的题目往往较长,解题时需认真阅读,从中提炼出有用信息,建立数学模型,转化为数学问题求解.
(2)当运用基本不等式求最值时,若等号成立的自变量不在定义域内时,就不能使用基本不等式求解,此时可根据变量的范围用对应函数的单调性求解.
(四)二次函数与方程、不等式
1.函数y=ax2+bx+c(a≠0)的图象与x轴的交点和相应方程ax2+bx+c=0(a≠0)的根的关系
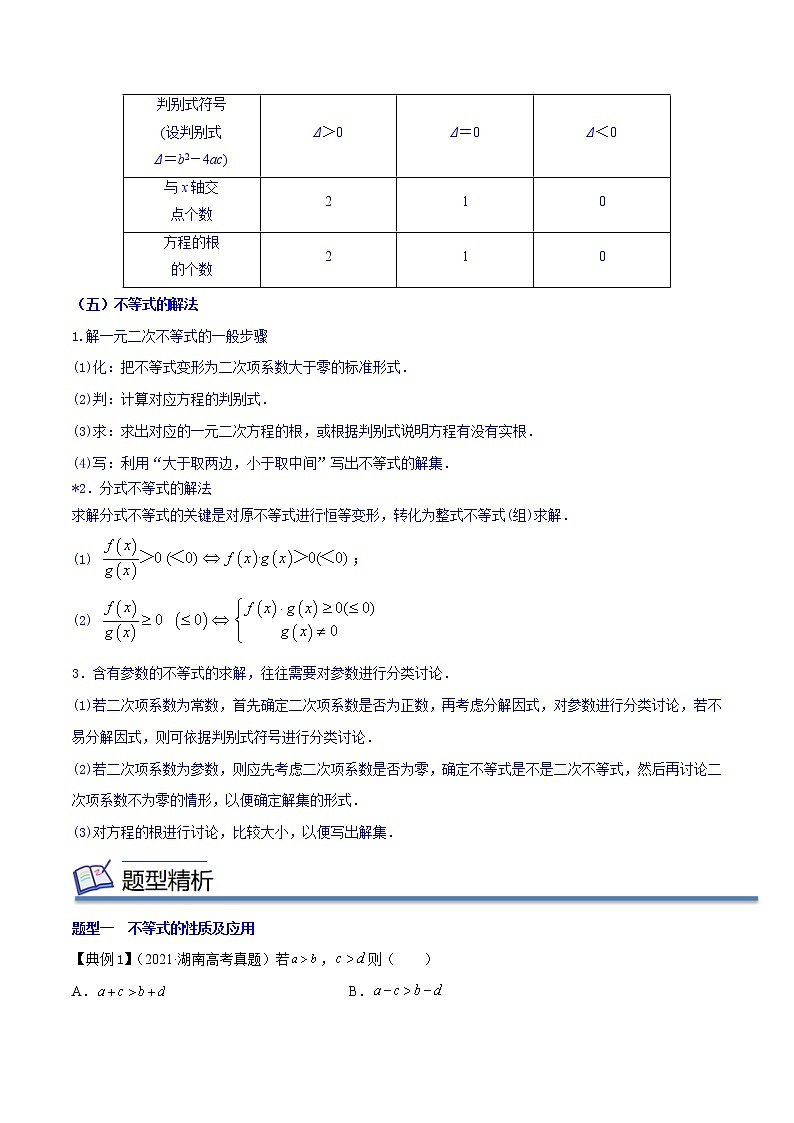
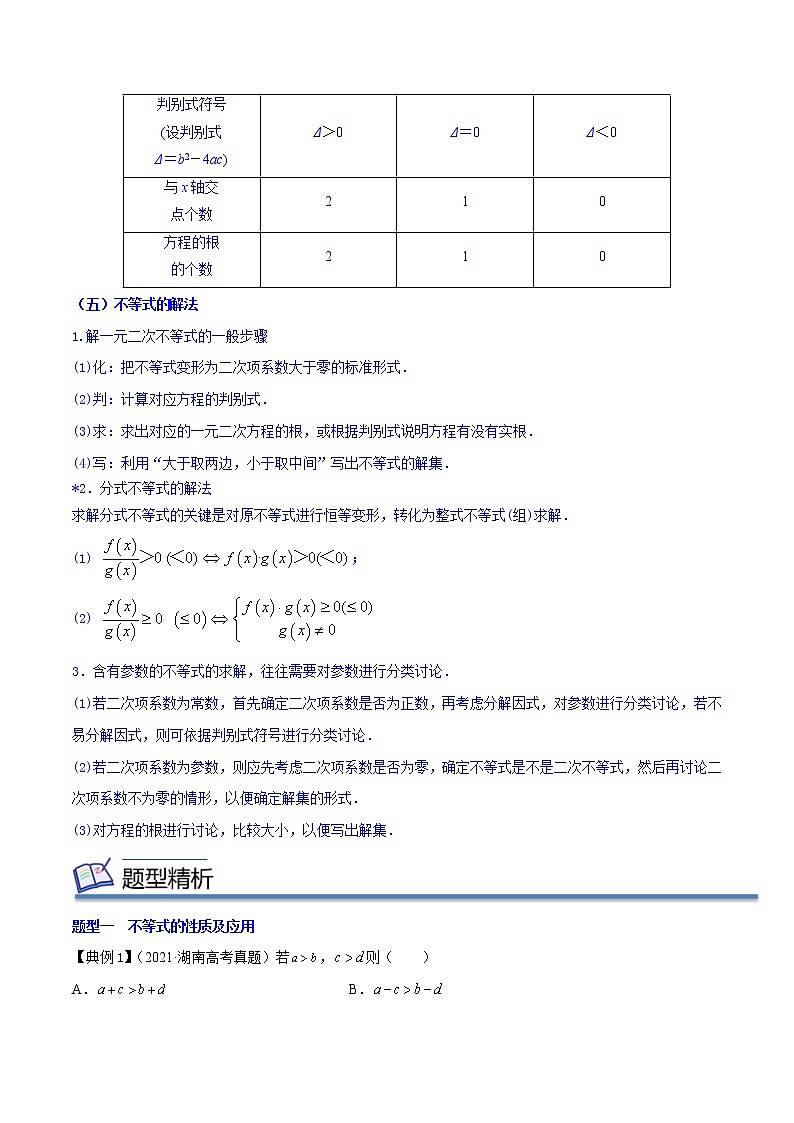
函数图象 | |||
判别式符号 (设判别式 Δ=b2-4ac) | Δ>0 | Δ=0 | Δ<0 |
与x轴交 点个数 | 2 | 1 | 0 |
方程的根 的个数 | 2 | 1 | 0 |
(五)不等式的解法
1.解一元二次不等式的一般步骤
(1)化:把不等式变形为二次项系数大于零的标准形式.
(2)判:计算对应方程的判别式.
(3)求:求出对应的一元二次方程的根,或根据判别式说明方程有没有实根.
(4)写:利用“大于取两边,小于取中间”写出不等式的解集.
*2.分式不等式的解法
求解分式不等式的关键是对原不等式进行恒等变形,转化为整式不等式(组)求解.
(1) ;
(2)
3.含有参数的不等式的求解,往往需要对参数进行分类讨论.
(1)若二次项系数为常数,首先确定二次项系数是否为正数,再考虑分解因式,对参数进行分类讨论,若不易分解因式,则可依据判别式符号进行分类讨论.
(2)若二次项系数为参数,则应先考虑二次项系数是否为零,确定不等式是不是二次不等式,然后再讨论二次项系数不为零的情形,以便确定解集的形式.
(3)对方程的根进行讨论,比较大小,以便写出解集.
题型一 不等式的性质及应用
【典例1】(2021·湖南高考真题)若,则( )
A. B.
C. D.
【典例2】(2020·慈溪中学高一月考)下列命题中正确的是( )
A.若,则 B.若,则
C.若,则 D.若,则
【典例3】(2022·江苏·高一)已知,,,则的大小关系为( )
A. B. C. D.无法确定
【典例4】(2022·江苏·南京市中华中学高一阶段练习)已知,.
(1)分别求a,c的取值范围;
(2)求的取值范围.
【特别提醒】
1.比较两个数或代数式的大小的三种方法
(1)当两个数(或式子)正负未知且为多项式时,用作差法.
步骤:①作差;②变形;③判断差的符号;④下结论.
变形技巧:①分解因式;②平方后再作差;③配方;④分子、分母有理化;⑤通分.
(2)作商法:要求两个数(或式子)为正数.
步骤:①作商;②变形;③判断商与1的大小;④下结论.
(3)特殊值法:对于比较复杂的代数式比较大小,利用不等式的性质不易比较大小时,可以采用特殊值法比较.
2.判断不等式是否成立的方法
(1)不等式性质法:直接利用不等式的性质逐个验证,利用不等式的性质时要特别注意前提条件.
(2)特殊值法:利用特殊值排除错误答案.
3.利用不等式的性质求取值范围的方法
(1)已知x,y的范围,求F(x,y)的范围.可利用不等式的性质直接求解.
(2)已知f(x,y),g(x,y)的范围,求F(x,y)的范围.
可利用待定系数法解决,即设F(x,y)=mf(x,y)+ng(x,y),用恒等变形求得m,n,再利用不等式的性质求得F(x,y)的取值范围.
题型二 利用基本不等式证明不等式
【典例5】【多选题】(2021·江苏扬州·高一期中)若,,,则下列不等式中对一切满足条件的,恒成立的是( )
A. B. C. D.
【典例6】【多选题】(2021·徐州市第三十六中学(江苏师范大学附属中学)高一期中)设a>0,b>0,则( )
A. B.
C. D.
【典例7】(2021·江苏·高一专题练习)已知均为正实数,且满足证明:
(1);
(2).
【方法技巧】
利用基本不等式证明不等式是综合法证明不等式的一种情况,要从整体上把握运用基本不等式,对不满足使用基本不等式条件的可通过“变形”来转换,常见的变形技巧有:拆项,并项,也可乘上一个数或加上一个数,“1”的代换法等.
题型三:利用基本不等式求最值
【典例8】【多选题】(2021·江苏·盐城市田家炳中学高一期中)以下结论正确的是( )
A.函数的最小值是2;
B.若且,则;
C.的最小值是2;
D.函数的最大值为0.
【典例9】(2021·江苏·姜堰中学高一期中)设,若,则的最大值是___________.
【典例10】(2022·江苏·高一)已知,,且,则的最小值是________.
【典例11】(2021·江苏省溧阳中学高一期中)设实数,若函数的最小值为6,则________.
【典例12】(2021·天津·高考真题)若,则的最小值为____________.
【规律方法】
1.利用基本不等式求最值的三种方法
2.利用均值不等式求最值遵循的原则:“一正二定三等”
(1)正:使用均值不等式所涉及的项必须为正数,如果有负数则考虑变形或使用其它方法
(2)定:使用均值不等式求最值时,变形后的一侧不能还含有核心变量.
(3)等:若能利用均值不等式求得最值,则要保证等号成立,要注意以下两点:
① 若求最值的过程中多次使用均值不等式,则均值不等式等号成立的条件必须能够同时成立(彼此不冲突)
② 若涉及的变量有初始范围要求,则使用均值不等式后要解出等号成立时变量的值,并验证是否符合初始范围.
题型四:基本不等式的实际应用
【典例13】(2021·江苏扬州·高一期中)为响应创建文明卫生城市的号召,某校计划在学校空地建设一个面积为的长方形花草坪,如图所示,花草坪中间设计一个矩形种植花卉,矩形上下各留左右各留种植草坪,设花草坪长度为(单位:),宽度为(单位:),矩形的面积为(单位:).
(1)试用表示;
(2)求的最大值,并求出此时的值.
【典例14】(2021·江苏高考真题)某化工厂引进一条先进生产线生产某种化工产品,其生产的总成本万元与年产量吨之间的函数关系可以近似地表示为,已知此生产线的年产量最小为60吨,最大为110吨.
(1)年产量为多少吨时,生产每吨产品的平均成本最低?并求最低平均成本;
(2)若每吨产品的平均出厂价为24万元,且产品能全部售出,则年产量为多少吨时,可以获得最大利润?并求最大利润.
【规律方法】
1.用均值不等式解决此类问题时,应按如下步骤进行:
(1)理解题意,设变量,设变量时一般把要求最大值或最小值的变量定为函数;
(2)建立相应的函数关系式,把实际问题抽象为函数的最大值或最小值问题;
(3)在定义域内,求出函数的最大值或最小值;
(4)正确写出答案.
2.利用基本不等式求解实际应用题注意点:
(1)此类型的题目往往较长,解题时需认真阅读,从中提炼出有用信息,建立数学模型,转化为数学问题求解.
(2)当运用基本不等式求最值时,若等号成立的自变量不在定义域内时,就不能使用基本不等式求解,此时可根据变量的范围用对应函数的单调性求解.
【易错警示】忽视不等式等号成立的条件!
题型五:二次函数的图象和性质的应用
【典例15】(2020·山东·高考真题)已知二次函数的图像如图所示,则不等式的解集是( )
A. B.
C. D.
【典例16】(2021·江苏·海安高级中学高一阶段练习)不等式的解集是,则下列结论正确的是( )
A. B.
C. D.
题型六:一元二次不等式的解法
【典例17】(2022·江苏省如皋中学高一开学考试)不等式的解集为( )
A.或 B.
C.或 D.
【典例18】(2022·江苏·高一专题练习)若不等式的解集为,则不等式的解集是( )
A. B.或
C. D.
【典例19】解不等式:ax2-(a+1)x+1<0.(a为实数)
【特别提醒】
含参不等式的解法:
(1)当判别式Δ能写成一个式子的平方的形式时,可先求方程的两根,再讨论两根的大小,从而写出解集.
(2)三个方面讨论:二次项系数的讨论,根有无的讨论,根大小的讨论.
(3)含参数分类讨论问题最后要写综述.
题型七:一元二次不等式恒成立问题
【典例20】(2021·四川省南充高级中学高二期中(文))若命题“,”是真命题,则实数的取值范围为_________.
【典例21】(2022·江苏·高一)设函数,若对于任意的,恒成立,则实数m的取值范围为______.
【规律方法】
一元二次不等式恒成立问题的解法
(1)函数法(图象法)
设f(x)=ax2+bx+c(a≠0).
①f(x)>0在x∈R上恒成立⇔a>0且Δ<0;
②f(x)<0在x∈R上恒成立⇔a<0且Δ<0;
③当a>0时,f(x)>0在x∈[α,β]上恒成立⇔ 或或
f(x)<0在x∈[α,β]上恒成立⇔
④当a<0时,f(x)>0在x∈[α,β]上恒成立⇔;f(x)<0在x∈[α,β]上恒成立⇔或或
(2)最值法
对于含参数的不等式恒成立问题,常通过分离参数,把求参数的范围问题转化为求函数的最值问题.
a>f(x)恒成立⇔a>f(x)max,
a<f(x)恒成立⇔a<f(x)min.
一、单选题
1.(2022·江苏·南京市中华中学高一阶段练习)下列结论正确的是( )
A.若,则 B.若,则
C.若,则 D.若,则
2.(2022·江苏·高一专题练习)已知二次函数的图象如图所示,则不等式的解集是( )
A. B.或 C. D.或
3.(2021·江苏·盐城市田家炳中学高一期中)不等式的解集是( )
A. B. C. D.或
4.(2022·江苏·南京市中华中学高一阶段练习)若命题“对任意的,恒成立”为假命题,则m的取值范围为( )
A. B. C. D.
5.(2022·江苏省如皋中学高一开学考试)命题“”为假命题,则实数的取值范围是( )
A.或 B.
C. D.
6.(2021·江苏·高一单元测试)已知,且,若恒成立,则实数的取值范围是( )
A.或 B.或
C. D.
7.(2022·江苏·高一)《几何原本》卷2的几何代数法(以几何方法研究代数问题)成了后世西方数学家处理问题的重要依据,通过这一原理,很多的代数的公理或定理都能够通过图形实现证明,也称之为无字证明.现有如图所示图形,点在半圆上,点在直径上,且,设,,则该图形可以完成的无字证明为( )
A. B.
C. D.
8.(2021·江苏·扬州大学附属中学高一期中)下列命题,错误的是( )
A.若,则的最小值为2 B.若,则的最小值为2
C.若,则的最小值为2 D.若,则的最小值为2
二、多选题
9.(2022·江苏省天一中学高一期末)已知、、、均为非零实数,则下列一定正确的有( )
A. B.
C.若,则 D.若,,则
10.(2022·江苏·高一专题练习)已知,,且,则( )
A.xy的取值范围是 B.的取值范围是
C.的最小值是3 D.的最小值是
11.(2020·江苏·明达中学高一阶段练习)在R上定义运算:,若不等式对任意实数恒成立,则实数的可能取值为( )
A. B. C. D.
12.(2022·江苏南通·高一开学考试)已知不等式的解集是,则下列四个结论中正确的是( ).
A.
B.若不等式的解集为,则
C.若不等式的解集为,则
D.若不等式的解集为,且,则
三、填空题
13.(2022·江苏省响水中学高一开学考试)已知正实数a,b满足,则的最小值为______.
14.(2021·江苏·无锡市市北高级中学高一期中)已知,,且满足,则的最大值为__________.
15.(2022·江苏·高一专题练习)已知不等式的解集是,,则不等式的解集是____________.
16.(2022·江苏·高一)已知,,,则的最小值为__.
四、解答题
17.(2020·江苏·明达中学高一阶段练习)设,,比较与的大小
18.(2021·江苏·盐城市田家炳中学高一期中)设全集,集合,集合,其中.
(1)当时,求;
(2)若“”是“”的充分条件,求的取值范围.
19.(2021·江苏·盐城市田家炳中学高一期中)若正数,,满足.
(1)求的最大值;
(2)求的最小值.
20.(2021·江苏·盐城市田家炳中学高一期中)已知不等式的解集为.
(1)求实数,的值;
(2)解关于的不等式(其中为实数).
21.(2021·江苏·扬中市第二高级中学高一期中)(1)已知,比较与的大小;
(2)已知正数,满足,证明:
22.(2022·江苏·高一)为宣传2022年北京冬奥会,某公益广告公司拟在一张矩形海报纸(记为矩形,如图)上设计三个等高的宣传栏(栏面分别为一个等腰三角形和两个全等的直角梯形),宣传栏(图中阴影部分)的面积之和为.为了美观,要求海报上所有水平方向和竖直方向的留空宽度均为.设直角梯形的高为.
(1)当时,求海报纸的面积;
(2)为节约成本,应如何选择海报纸的尺寸,可使用纸量最少(即矩形的面积最小)?
【寒假作业】苏教版2019 高中数学 高一寒假提升训练 专题03 不等式(14大考点,知识串讲+热考题型+专题训练)-: 这是一份【寒假作业】苏教版2019 高中数学 高一寒假提升训练 专题03 不等式(14大考点,知识串讲+热考题型+专题训练)-,文件包含寒假作业苏教版2019高中数学高一寒假提升训练专题03不等式14大考点知识串讲+热考题型+专题训练原卷版讲义docx、寒假作业苏教版2019高中数学高一寒假提升训练专题03不等式14大考点知识串讲+热考题型+专题训练解析版讲义docx等2份试卷配套教学资源,其中试卷共53页, 欢迎下载使用。
专题03 计数原理、排列、组合(知识串讲 热考题型 专题训练)-2022-2023学年高二数学下学期期中期末考点大串讲(苏教版2019选择性必修第二册): 这是一份专题03 计数原理、排列、组合(知识串讲 热考题型 专题训练)-2022-2023学年高二数学下学期期中期末考点大串讲(苏教版2019选择性必修第二册),文件包含专题03计数原理排列组合解析版docx、专题03计数原理排列组合原卷版docx等2份试卷配套教学资源,其中试卷共63页, 欢迎下载使用。
专题03 排列与组合(知识串讲 热考题型 专题训练)-2022-2023学年高二数学下学期期中期末考点大串讲(人教A版2019): 这是一份专题03 排列与组合(知识串讲 热考题型 专题训练)-2022-2023学年高二数学下学期期中期末考点大串讲(人教A版2019),文件包含专题03排列与组合解析版docx、专题03排列与组合原卷版docx等2份试卷配套教学资源,其中试卷共41页, 欢迎下载使用。












